2017年吉林省长春市中考数学模拟试卷（8）

试卷更新日期：2017-08-07 类型：中考模拟

进入出卷网下载

一、选择题

1. 比﹣3大2的数是（）

A、﹣5 B、﹣1 C、1 D、5

查看试题解析
2. 下列计算正确的是（　　）

A、a+2a=3a² B、a•a²=a³ C、（2a）²=2a² D、（﹣a²）³=a⁶

查看试题解析
3. 如图，由五个完全相同的小正方体组合成一个立体图形，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
4. 一次数学考试后，小明想知道成绩是否能排在前一半，那么他应该知道本次成绩的统计量是（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
5. 如图，小手盖住的点的坐标可能为（）

A、（5，2） B、（﹣6，3） C、（﹣4，﹣6） D、（3，﹣4）

查看试题解析
6. 小华拿24元钱购买火腿肠和方便面，已知一盒方便面3元，一根火腿肠2元，他买了4盒方便面，x根火腿肠，则关于x的不等式表示正确的是（）

A、3×4+2x＜24 B、3×4+2x≤24 C、3x+2×4≤24 D、3x+2×4≥24

查看试题解析
7. 如图，点A在函数y= $\frac{2}{x}$ （x＞0）的图象上，点B在函数y= $\frac{4}{x}$ （x＞0）的图象上，且AB∥x轴，BC⊥x轴于点C，则四边形ABCO的面积为（）

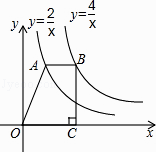A、1 B、2 C、3 D、4

查看试题解析
8.
若一次函数y=kx+b的图象如图所示，则k，b的值可能为（）

A、k=3，b=3 B、k=3，b=﹣3 C、k=﹣3，b=3 D、k=﹣3，b=﹣3

查看试题解析

二、填空题

9. 计算： $\sqrt{18} + \sqrt{2}$ = ．

查看试题解析
10. 方程 $\frac{x}{x + 1}$ =2的解是x= ．

查看试题解析
11. 在平面直角坐标系中，点A（1，2）关于y轴对称的点为B（a，b），则a= ．

查看试题解析
12. 二次函数y=x²+bx+c中，函数y与自变量x的部分对应值如下表，则m的值为．
x
﹣2
﹣1
0
1
2
3
4
y
7
2
﹣1
﹣2
m
2
7

查看试题解析
13. 如图，正五边形ABCDE内接于⊙O，若⊙O的半径为5，则弧AB的长为．

查看试题解析
14. 如图1，是我们平时使用的等臂圆规，即CA=CB．若n个相同规格的等臂圆规的两脚依次摆放在同一条直线上如图2所示，其张角度数变化如下：∠A₁C₁A₂=160°，∠A₂C₂A₃=80°，∠A₃C₃A₄=40°，∠A₄C₄A₅=20°，…．，根据上述规律请你写出∠A_n₊₁A_nC_n=°．（用含n的代数式表示）

查看试题解析

三、解答题

15. 先化简，再求值： $\frac{x^{2} + 2 x + 1}{x^{2} - 1} - \frac{1}{x - 1}$ ，其中 $x = \sqrt{2} + 1$ ．

查看试题解析
16. 将5个完全相同的小球分装在甲、乙两个不透明的口袋中．甲袋中有3个球，分别标有数字2，3，4；乙袋中有2个球，分别标有数字2，4．从甲、乙两个口袋中各随机摸出一个球．

(1)、用列表法或画树状图法，求摸出的两个球上数字之和为5的概率．

(2)、摸出的两个球上数字之和为多少时的概率最大？

查看试题解析
17. 海南五月瓜果飘香，某超市出售的“无核荔枝”和“鸡蛋芒果”单价分别为每千克26元和22元，李叔叔购买这两种水果共30千克，共花了708元．请问李叔叔购买这两种水果各多少千克？

查看试题解析
18. 如图，已知直线a，b及∠POQ，以点O为圆心，a为半径作圆，交∠POQ两边于点M，N，再分别以点M，N为圆心，b为半径画弧，两弧交于点A，连结OA，MA，NA，则∠AMO=∠ANO，请证明．

查看试题解析
19.
如图，小明想测山高度，他在B处仰望山顶A，测得仰角∠B=31°，再往山的方向（水平方向）前进80m至索道口C处，沿索道方向仰望山顶，测得仰角∠ACE=39°．求这座山的高度（小明的身高忽略不计）．

【参考数据：tan31°≈ $\frac{3}{5}$ ，sin31°≈ $\frac{1}{2}$ ，tan39°≈ $\frac{9}{11}$ ，sin39°≈ $\frac{7}{11}$ 】

查看试题解析
20. 为了了解某市初中学生上学的交通方式，从中随机调查了a名学生的上学交通方式，统计结果如图．

(1)、求a的值；

(2)、补全条形统计图并求出乘坐公共汽车上学占上学交通方式百分比的扇形圆心角的度数；

(3)、该市共有初中学生15000名，请估计其中坐校车上学的人数．

查看试题解析
21. 一慢车和一快车沿相同路线从A地到B地，所行的路程与时间的函数图象如图所示．请你根据图象，回答下列问题：

(1)、慢车比快车早出发小时，快车追上慢车时行驶了千米，快车比慢车早小时到达B地；

(2)、在下列3个问题中任选一题求解（多做不加分）：
①快车追上慢车需几个小时？
②求慢车、快车的速度；
③求A、B两地之间的路程．

查看试题解析
22. 定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．

(1)、
已知：如图1，四边形ABCD是“等对角四边形”，∠A≠∠C，∠A=70°，∠B=80°．求∠C，∠D的度数．

(2)、
在探究“等对角四边形”性质时：张同学画了一个“等对角四边形”ABCD（如图2），其中∠ABC=∠ADC，AB=AD，此时她发现CB=CD成立．请你证明此结论；

(3)、已知：在“等对角四边形”ABCD中，∠DAB=45°，∠ABC=90°，AB=5，AD=4 $\sqrt{2}$ ．则对角线AC的长为．

查看试题解析
23.
如图，抛物线l₁：y=x²﹣4的图象与x轴交于A，C两点，抛物线l₂与l₁关于x轴对称．

(1)、直接写出l₂所对应的函数表达式；

(2)、若点B是抛物线l₂上的动点（B与A，C不重合），以AC为对角线，A，B，C三点为顶点的平行四边形的第四个顶点为D，求证：D点在l₂上．

(3)、当点B位于l₁在x轴下方的图象上，平行四边形ABCD的面积是否存在最大值和最小值？若存在，判断它是何种特殊平行四边形，并求出它面积的最值；若不存在，请说明理由．

查看试题解析
24.
已知：Rt△ABC中，∠ACB=90°，CA=3，CB=4，设P，Q分别为AB边，CB边上的动点，它们同时分别从A，C出发，以每秒1个单位长度的速度向终点B运动，设P，Q运动的时间为t秒．

(1)、求△CPQ的面积S与运动时间t之间的函数关系式，并求出S的最大值．

(2)、t为何值时，△CPQ为直角三角形．

(3)、①探索：△CPQ是否可能为正三角形，说明理由．
②P，Q两点同时出发，若点P的运动速度不变，试改变点Q的运动速度，使△CPQ为正三角形，求出点Q的运动速度和此时的t值．

查看试题解析

x	﹣2	﹣1	0	1	2	3	4
y	7	2	﹣1	﹣2	m	2	7