四川省金堂县2016-2017学年八年级下学期期末考试数学试题
试卷更新日期:2017-08-07 类型:期末考试
一、选择题
-
1. 观察出下列四种汽车标志,其中既是中心对称图形,又是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 若x>y,则下列式子中错误的是( )A、x-3>y-3 B、 C、x+3>y+3 D、-3x>-3y3. 若分式 有意义,则 应满足的条件是( ).A、x≠0 B、x≠-3 C、x≥-3 D、x≤-34. 下列四个多项式中,能因式分解的是( ).A、a2+1 B、x2+5y C、x2﹣5y D、a2﹣6a+95. 若一个正多边形的一个外角为45°,则这个正多边形的边数是( )A、6 B、7 C、8 D、96. 不等式组 的解集在数轴上表示正确的是( )A、
2. 若x>y,则下列式子中错误的是( )A、x-3>y-3 B、 C、x+3>y+3 D、-3x>-3y3. 若分式 有意义,则 应满足的条件是( ).A、x≠0 B、x≠-3 C、x≥-3 D、x≤-34. 下列四个多项式中,能因式分解的是( ).A、a2+1 B、x2+5y C、x2﹣5y D、a2﹣6a+95. 若一个正多边形的一个外角为45°,则这个正多边形的边数是( )A、6 B、7 C、8 D、96. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、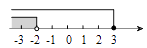 C、
C、 D、
D、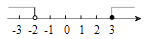 7. 分式方程 的解为( )
7. 分式方程 的解为( )
A、 B、 C、 D、8.如图,在△ABC中,AC=10,BC=8,AB垂直平分线交AB于点M , 交AC于点D , 则△BDC的周长为( )
 A、14 B、16 C、18 D、209.
A、14 B、16 C、18 D、209.如图,在▱ABCD中,AC、BD相交于点O , 点E是AB的中点.若OE=1cm , 则AD的长是( )cm .
 A、2 B、3 C、4 D、510.
A、2 B、3 C、4 D、510.如图,直线y=x+b与直线y=kx+6交于点P(1,3),则关于x的不等式x+b>kx+6的解集是( ).
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式: -9= .12. 不等式 的正整数解是;13. 若关于 有增根,则 =;14.
如图,在▱ABCD中,AB=13,AD=10,将▱ABCD沿AE翻折后,点B恰好与点C重合,则折痕AE的长为;
 15. 若 ,则 ;16.
15. 若 ,则 ;16.有5张正面分别标有数字-2,0,2,4,6的不透明卡片,它们除数不同外其余全部相同,先将它们背面朝上,洗匀后从中任取一张,将该卡片上的数字记为
 ,则使关于
,则使关于  不等式组 有实数解的概率为;17. 若关于x的方程 ;
不等式组 有实数解的概率为;17. 若关于x的方程 ;
18.如图,等边三角形△ABC的边长为4,过点C的直线 ⊥AC , 且△ABC与△A′B′C关于直线 对称,D为线段BC′上一动点,则AD+BD的最小值是;
 19.
19.一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1 , E1 , E2 , C2 , E3 , E4 , C3……在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3……则正方形A2017B2017C2017D2017的边长是;

三、解答题
-
20. 综合题。(1)、解不等式组:(2)、解方程: .21. 综合题。(1)、分解因式:(2)、化简: .22.
如图,在▱ABCD中,∠ABC的平分线交AD于点E , 过点D作BE的平行线交于BC于F .
 (1)、求证:△ABE≌△CDF;(2)、若AB=6,BC=8,求DE的长.23.
(1)、求证:△ABE≌△CDF;(2)、若AB=6,BC=8,求DE的长.23.如图,在边长为1的小正方形网格中,△AOB的顶点均在格点上,
 (1)、B点关于y轴的对称点坐标为;(2)、将△AOB向左平移3个单位长度得到△A1O1B1 , 请画出△A1O1B1;(3)、以原点O为对称中心,画出△ AOB与关于原点对称的△ A2 O B2;(4)、以原点O为旋转中心,画出把△AOB顺时针旋转90°的图形△A3 O B3 .24. 某工厂甲、乙两人加工同一种零件,每小时甲比乙多加工10个这种零件,甲加工150个这种零件所用的时间与乙加工120个这种零件所用的时间相等,(1)、甲、乙两人每小时各加工多少个这种零件?(2)、该工厂计划加工920个零件,甲参与加工这批零件不超过12天,则乙至少加工多少天才能加工完这批零件?25.
(1)、B点关于y轴的对称点坐标为;(2)、将△AOB向左平移3个单位长度得到△A1O1B1 , 请画出△A1O1B1;(3)、以原点O为对称中心,画出△ AOB与关于原点对称的△ A2 O B2;(4)、以原点O为旋转中心,画出把△AOB顺时针旋转90°的图形△A3 O B3 .24. 某工厂甲、乙两人加工同一种零件,每小时甲比乙多加工10个这种零件,甲加工150个这种零件所用的时间与乙加工120个这种零件所用的时间相等,(1)、甲、乙两人每小时各加工多少个这种零件?(2)、该工厂计划加工920个零件,甲参与加工这批零件不超过12天,则乙至少加工多少天才能加工完这批零件?25.如图,△ABC和△DBE均为等腰三角形,点A , D,E在同一直线上,连接CE .
 (1)、如图1,若∠BAC=∠BCA=∠BDE=∠BED=55°
(1)、如图1,若∠BAC=∠BCA=∠BDE=∠BED=55°①求证:AD=CE;
②求∠AEC的度数.
(2)、如图2,若∠ABC=∠DBE=120°,BM为△BDE中DE边上的高,CN为△ACE中AE边上的高, 试证明:AE= .26.金堂骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,某车行经营的A型车去年2月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年2月份与去年2月份卖出的A型车数量相同,则今年2月份A型车销售总额将比去年2月份销售总额增加25%.
 (1)、求今年2月份A型车每辆销售价多少元?(2)、该车行计划今年3月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的2倍,A、B两种型号车的进货和销售价格如下表,问应如何进货才能使这批车获利最多?27.
(1)、求今年2月份A型车每辆销售价多少元?(2)、该车行计划今年3月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的2倍,A、B两种型号车的进货和销售价格如下表,问应如何进货才能使这批车获利最多?27.如图,四边形ABCD是正方形,在AB的延长线上取一点E,连接EC,过点C作CF⊥EC交AD于F.

 (1)、求证:EC=FC.(2)、若G、M分别是AB、CD上一动点,连接GM.H是GM上的中点,连接BH,当G、M运动到某一特殊位置时得到BH=BG+CM,此时∠ABH的度数是多少?请说明理由.(3)、在(2)的条件下,若BG=1,MC= ,连接AH.求出四边形△AHMD的面积.28.
(1)、求证:EC=FC.(2)、若G、M分别是AB、CD上一动点,连接GM.H是GM上的中点,连接BH,当G、M运动到某一特殊位置时得到BH=BG+CM,此时∠ABH的度数是多少?请说明理由.(3)、在(2)的条件下,若BG=1,MC= ,连接AH.求出四边形△AHMD的面积.28.如图,边长为 正方形OABC的边OA、OC在坐标轴上.在 轴上线段 (Q在A的右边),P从A出发,以每秒1个单位的速度向O运动,当点P到达点O时停止运动,运动时间为 .连接PB,过P作PB的垂线,过Q作 轴的垂线,两垂线相交于点D.连接BD交 轴于点E,连接PD交 轴于点F,连接PE.
 (1)、求∠PBD的度数.(2)、设△POE的周长为 ,探索 与 的函数关系式,并写出 的取值范围.(3)、
(1)、求∠PBD的度数.(2)、设△POE的周长为 ,探索 与 的函数关系式,并写出 的取值范围.(3)、令
 ,当△PBE为等腰三角形时,求△EFD的面积.
,当△PBE为等腰三角形时,求△EFD的面积.