重庆市2017年新课标•华东师大版数学实验教材八年级下学期期末测试数学卷

试卷更新日期：2017-08-07 类型：期末考试

进入出卷网下载

一、选择题

1. 将数49开平方，其结果是（）

A、±7 B、-7 C、7 D、 $\sqrt{49}$

查看试题解析
2. 结合函数y=-2x的图象回答，当x＜-1时，y的取值范围（）

A、y＜2 B、y＞2 C、y≥ $\frac{1}{2}$ D、y≤ $\frac{1}{2}$

查看试题解析
3. 已知∠α的顶点在原点，一条边在x轴的正半轴，另一条边经过点P(3，-4)，则sinα的值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{4}{5}$ D、 $\frac{3}{5}$

查看试题解析
4.
如图，两条宽度都是1的纸条，交叉重叠放在一起，且夹角为α，则重叠部分的面积为（）

A、 $\frac{1}{sin α}$ B、 $\frac{1}{cos α}$ C、tanα D、1

查看试题解析
5. 为了判断甲乙两个小组学生英语口语测验成绩哪一组整齐，通常需要知道两组成绩的（）

A、平均数 B、方差 C、众数 D、频率分布

查看试题解析
6. 要使式子 $\sqrt{2 x - 4}$ 有意义，字母x应满足的条件为（）

A、x＞2 B、x＜2 C、x≥2 D、x＞-2

查看试题解析
7. 若点P(m,2)与点Q(3,n)关于原点对称，则m、n的值分别为（）.

A、-3,2 B、3, -2 C、–3, -2 D、3, 2

查看试题解析
8. 直线y=3x与双曲线的一个分支 $y = \frac{k}{x}$ (k≠0、x>0)相交，则该分支所在象限为（）

A、1 B、2 C、3 D、4

查看试题解析
9. 如果把三角形的三边按一定的比例扩大，则下列说法正确的是（）

A、三角形的形状不变，三边的比变大 B、三角形的形状变，三边的比变大 C、三角形的形状变，三边的比不变 D、三角形的形状不变，三边的比不变

查看试题解析
10. 在Rt△ABC中，若各边的长度同时扩大5倍，那么锐角A的正弦值和余弦值（）

A、都不变 B、都扩大5倍 C、正弦扩大5倍、余弦缩小5倍 D、不能确定

查看试题解析

二、填空题

11. $2 \sqrt{75} - 3 \sqrt{27} + \sqrt{3}$ 的结果是.

查看试题解析
12. 已知 $| 2 x + 1 | + \sqrt{2 - y} = 0$ ，那么(xy)²⁰⁰⁵=

查看试题解析
13. 如果点M(a+1，2-a)在第一象限内，则a的取值范围是

查看试题解析
14. 设点P（x，y）在第二象限，且 $| x | = 1, | y | = 2$ ，则P点的坐标为

查看试题解析
15. 某种中性笔一盒12支，售价18元，可零卖，小明买了x支，付款为y元，那么y与x的函数关系式是.

查看试题解析
16. 在△ABC和△A₁B₁C₁中，若 $\frac{A B}{A_{1} B_{1}} = \frac{B C}{B_{1} C_{1}} = \frac{1}{2}$ ，且∠B=∠B₁=56°，则 $\frac{S_{Δ A B C}}{S_{Δ A_{1} B_{1} C_{1}}}$ =。

查看试题解析
17.
如图：在坡度为1：2的山坡上种树，要求株距（水平距离）为6米，则斜坡上相邻两树间的坡面距离为

查看试题解析
18. 在离旗杆20米处的地方用测角仪测得旗杆顶的仰角为α，如果测角仪的高度为1.5米，那么旗杆的高度为(用含α的代数式表示)

查看试题解析
19. 正方形ABCD的边长为1，如果将线段BD绕着点B旋转后，点D落在BC延长线上的点D₁处，那么tan∠BAD₁=

查看试题解析
20. 一个样本含有20个数据：68、69、70、66、68、64、65、65、69、62、67、66、65、67、63、65、64、61、65、66，在列频率分布表时，如果组距为2，那么应分为组，在64.5～66.5这一小组的频率为

查看试题解析

三、解答题

21. 计算： $(\sqrt{108} - \sqrt{45}) - 8 \sqrt{\frac{1}{3}} - (\frac{4}{\sqrt{3}} + 6 \sqrt{\frac{4}{3}})$

查看试题解析
22. 计算 $(\sqrt{a^{3} b} + \sqrt{a b^{3}} + a b) \div \sqrt{a b}$

查看试题解析
23. 已知等腰三角形的周长为12，底边为y，腰长为x，求y与x的函数关系式，并求自变量x的取值范围

查看试题解析
24.
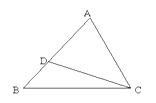
如图，在△ABC和△ACD中，在什么条件下，△ABC和△ACD相似?并说明理由.

查看试题解析
25. 某风景区集体门票的收费标准是：20人以内(含20人)，每人25元；超过20人，超过部分每人10元

(1)、写出应收门票费y(元)与游览人数x(人)之间的函数关系式

(2)、利用(1)中的函数关系式计算，某班54人去该风景区旅游时，为购门票共花了多少元?

查看试题解析
26.
在1998年的特大洪水期间，为了加固一段大堤，需运来沙石和土将大堤堤面加宽1米，使背水坡的坡度由原来的1：2变为1：3，已知原来背水坡的坡长为BC=15米，堤长100米，那么需要的沙石和土多少方?

查看试题解析
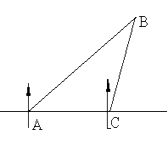
27.
一船在A处测得北偏东45°方向有一灯塔B，船向正东方向以每小时20海里的速度航行1.5小时到达C处时，又观测到灯塔B在北偏东15°方向上，求此时航船与灯塔相距多少海里?

查看试题解析
28.
如图，在△OAB中，O为坐标原点，横、纵轴的单位长度相同，A、B的坐标分别为(8，6)，(16，0)，点P沿OA边从点O开始向终点A运动，速度每秒1个单位，点Q沿BO边从B点开始向终点O运动，速度每秒2个单位，如果P、Q同时出发，用t(秒)表示移动时间，当这两点中有一点到达自己的终点时，另一点也停止运动。求：

(1)、几秒时PQ∥AB.

(2)、设△OPQ的面积为y，求y与t的函数关系式.

(3)、△OPQ与△OAB能否相似?若能，求出点P的坐标，若不能，试说明理由.

查看试题解析