内蒙古鄂尔多斯市鄂托克旗2016-2017学年八年级下学期期末考试数学试题
试卷更新日期:2017-08-07 类型:期末考试
一、选择题
-
1. 式子y= 中x的取值范围是( )A、x≥0 B、x≥0且x≠1 C、0≤x<1 D、x>12. 商厦信誉楼女鞋专柜试销一种新款女鞋,一个月内销售情况如下表所示:
型号(cm)
22
22.5
23
23.5
24
24.5
25
数量(双)
2
6
11
15
7
3
4
经理最关心的是,哪种型号的鞋销量最大.对他来说, 下列统计量中最重要的是. ( )
A、众数 B、平均数 C、中位数 D、方差3. 将下列长度的三根木棒首尾顺次连接,不能组成直角三角形的是. ( )A、1, , B、5,12,13 C、6,8,10 D、 , ,4. 将直线y=2x+3向下平移4个单位长度,得到的直线的函数表达式是( )A、y=2x﹣1 B、y=2x+1 C、y=﹣4x+3 D、y=2x+75.直线y= x+4与x轴、y轴分别交于点A和点B , 点C , D分别为线段AB , OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( ).
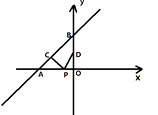 A、(-3,0) B、(-6,0) C、(- ,0) D、(- ,0)6.
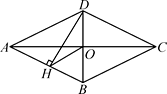
A、(-3,0) B、(-6,0) C、(- ,0) D、(- ,0)6.四边形ABCD是菱形,对角线AC , BD相交于点O , DH⊥AB于H , 连接OH , ∠DHO=20°,则∠CAD的度数是. ( )
 A、25° B、20° C、30° D、40°7.
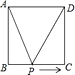
A、25° B、20° C、30° D、40°7.如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm)在下列图象中,表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是. ( )
 A、
A、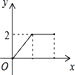 B、
B、 C、
C、 D、
D、 8. 下列计算正确的是( )A、 B、 C、 D、9. 已知点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=﹣3x+2上,则y1 , y2 , y3的值的大小关系是( )A、y3<y1<y2 B、y1<y2<y3 C、y3>y1>y2 D、y1>y2>y310. 下列命题中,错误的是( ).A、平行四边形的对角线互相平分 B、菱形的对角线互相垂直平分 C、矩形的对角线相等且互相垂直平分 D、角平分线上的点到角两边的距离相等
8. 下列计算正确的是( )A、 B、 C、 D、9. 已知点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=﹣3x+2上,则y1 , y2 , y3的值的大小关系是( )A、y3<y1<y2 B、y1<y2<y3 C、y3>y1>y2 D、y1>y2>y310. 下列命题中,错误的是( ).A、平行四边形的对角线互相平分 B、菱形的对角线互相垂直平分 C、矩形的对角线相等且互相垂直平分 D、角平分线上的点到角两边的距离相等二、填空题
-
11. 若y=(a+3)x+a2﹣9是正比例函数,则a=12.
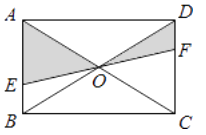
如图所示,EF过矩形ABCD对角线的交点O,且分别交AB,CD于点E,F,如果矩形的面积为1那么阴影部分的面积是
 13. 如果 (a、b为有理数),则a+b=14.
13. 如果 (a、b为有理数),则a+b=14.如图,在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是 .
 15.
15.观察下列一系列由火柴棒摆成的图案,第n个图案共需火柴棒根.
 16.
16.如图,O为数轴原点,A,B两点分别对应﹣3与3,作腰长为4的等腰△ABC,连接OC,以O为圆心,OC长为半径画弧交数轴于点M,则点M对应的实数为 .

三、解答题
-
17. 计算:(1)、(2)、÷ ﹣4× ×(1﹣ ) 0
18.如图,是一块四边形绿地的示意图,其中AB长为24米,BC长15米,CD长为20米,DA长7米,∠C=90°,求绿地ABCD的面积.
 19.
19.在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下两幅统计图.请根据相关信息,解答下列问题:
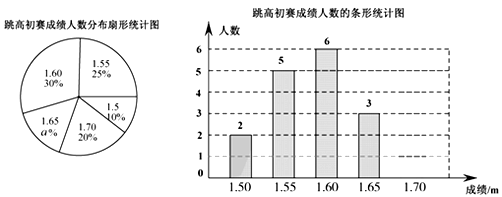 (1)、扇形统计图中a= , 初赛成绩为1.70m所在扇形图形的圆心角为(2)、补全条形统计图;(3)、这组初赛成绩的众数是m,中位数是;(4)、根据这组初赛成绩确定8人进入复赛,那么初赛成绩为1.65m的运动员杨强能否进入复赛?为什么?20.
(1)、扇形统计图中a= , 初赛成绩为1.70m所在扇形图形的圆心角为(2)、补全条形统计图;(3)、这组初赛成绩的众数是m,中位数是;(4)、根据这组初赛成绩确定8人进入复赛,那么初赛成绩为1.65m的运动员杨强能否进入复赛?为什么?20.如图,已知菱形ABCD的对角线AC 、BD相交于点O , 延长AB至点E , 使BE=AB , 连接CE .
 (1)、求证:四边形BECD是平行四边形;(2)、若∠E=60°,AC= ,求菱形ABCD的面积.21.
(1)、求证:四边形BECD是平行四边形;(2)、若∠E=60°,AC= ,求菱形ABCD的面积.21.如图,直线l1:y1=− x+m与y轴交于点A(0,6),直线l2:y2=kx+1分别与x轴交于点B(-2,0),与y轴交于点C.两条直线相交于点D,连接AB.
 (1)、求两直线交点D的坐标;(2)、求△ABD的面积;(3)、根据图象直接写出y1>y2时自变量x的取值范围.22. 某校计划购买甲、乙两种树苗共1000株用于绿化校园,甲种树苗每株25元,乙种树苗每株30元,通过调查了解,甲,乙两种树苗成活率分别是90%和95%.(1)、若购买这种树苗共用去28000元,则甲、乙两种树苗各购买多少株?(2)、要使这批树苗的总成活率不低于92%,则甲种树苗最多购买多少株?(3)、在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.23.
(1)、求两直线交点D的坐标;(2)、求△ABD的面积;(3)、根据图象直接写出y1>y2时自变量x的取值范围.22. 某校计划购买甲、乙两种树苗共1000株用于绿化校园,甲种树苗每株25元,乙种树苗每株30元,通过调查了解,甲,乙两种树苗成活率分别是90%和95%.(1)、若购买这种树苗共用去28000元,则甲、乙两种树苗各购买多少株?(2)、要使这批树苗的总成活率不低于92%,则甲种树苗最多购买多少株?(3)、在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.23.甲、乙两组同时加工某种零件,乙组工作中有一次停产更换设备,更换设备后,乙组的工作效率是原来的2倍.两组各自加工零件的数量y(件)与时间x(时)的函数图象如图所示.
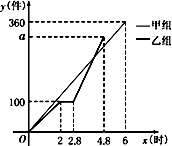 (1)、直接写出甲组加工零件的数量y与时间x之间的函数关系式;(2)、求乙组加工零件总量a的值;24.
(1)、直接写出甲组加工零件的数量y与时间x之间的函数关系式;(2)、求乙组加工零件总量a的值;24.已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边做正方形ADEF,连接CF
 (1)、如图1当点D在线段BC上时.求证:CF+CD=BC;
(1)、如图1当点D在线段BC上时.求证:CF+CD=BC;
(2)、如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;(3)、如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变①请直接写出CF,BC,CD三条线段之间的关系;②若正方形ADEF的边长为2 ,对角线AE,DF相交于点O,连接OC.求OC的长度.