江苏省连云港市灌云县2016-2017学年八年级下学期期末考数学试题

试卷更新日期：2017-08-07 类型：期末考试

进入出卷网下载

一、选择题

1. 若式子 $\sqrt{a - 3}$ 在实数范围内有意义，则a的取值范围是（）

A、a＞3 B、a≥3 C、a＜3 D、a≤3

查看试题解析
2. 要反映一个家庭在教育方面支出占总收入的比，宜采用（）

A、条形统计图 B、扇形统计图 C、折线统计图 D、频数分布直方图

查看试题解析
3. 桌上倒扣着背面相同的5张扑克牌，其中3张黑桃、2张红桃．从中随机抽取一张，则（　　）

A、能够事先确定抽取的扑克牌的花色 B、抽到黑桃的可能性更大 C、抽到黑桃和抽到红桃的可能性一样大 D、抽到红桃的可能性更大

查看试题解析
4. 为了了解在校学生参加课外兴趣小组活动情况，随机调查了40名学生，结果书法、绘画、舞蹈及其他的频数分别为8、11、12、9，则参加书法兴趣小组的频率是（）

A、0.1 B、0.15 C、0.2 D、0.3

查看试题解析
5. 反比例函数y= $\frac{k}{x}$ 的图象经过点M（﹣1，2），则反比例函数的解析式为（）

A、y=﹣ $\frac{1}{2 x}$ B、y= $\frac{1}{2 x}$ C、y=﹣ $\frac{2}{x}$ D、y= $\frac{2}{x}$

查看试题解析
6. 根据分式的基本性质，分式 $\frac{- a}{a - b}$ 可以变形为（）

A、 $\frac{a}{- a + b}$ B、 $\frac{a}{a + b}$ C、﹣ $\frac{- a}{a - b}$ D、﹣ $\frac{a}{a + b}$

查看试题解析
7. 若关于x的方程 $\frac{2 - x}{x - 5}$ + $\frac{m}{x - 5}$ =0有增根，则m的值是（）

A、﹣2 B、﹣3 C、5 D、3

查看试题解析
8.
如图，在菱形ABCD中，∠A=100°，E，F分别是边AB和BC的中点，EP⊥CD于点P，则∠FPC的度数为（）

A、50° B、55° C、60° D、45°

查看试题解析

二、填空题

9. 为了了解淮安市八年级学生的身高情况，从中任意抽取2000名学生的身高进行统计，在这个问题中，样本容量是．

查看试题解析
10. 小红说：“明天下雨”，你认为这是（填“随机事件”、“不可能事件”或“必然事件”）．

查看试题解析
11. 化简 $\sqrt{45}$ 的结果为．

查看试题解析
12. 化简 $\frac{1}{x - 1}$ + $\frac{x}{1 - x}$ = ．

查看试题解析
13. 已知反比例函数y= $\frac{2}{x}$ ，当1＜x≤3时，则y的取值范围是．

查看试题解析
14.
反比例函数在第一象限内的图象如图所示，点P是图象上的一点PQ⊥x轴，垂足为Q，△OPQ的面积为2，则k= ．

查看试题解析
15.
如图，点D、E是AB、AC边的中点，AH是△ABC的高，DE=a，AH=b，△ABC的面积为12，则a与b的函数关系式是：．

查看试题解析
16. 已知四边形ABCD为平行四边形，要使得四边形ABCD为矩形，则可以添加一个条件为．

查看试题解析
17.
如图，平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=6，AB=5，则AE的长为．

查看试题解析
18.
如图，在平面直角坐标系中，直线y=﹣4x+4与x轴、y轴分别交于A、B两点，以AB为边在第一象限作正方形ABCD，将正方形ABCD沿x轴负方向平移a个单位长度后，点C恰好落在双曲线在第一象限的分支上，则a的值是．

查看试题解析

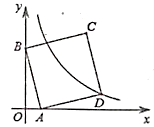
三、解答题

19. 计算：

(1)、 $\sqrt{12} + \frac{1}{\sqrt{3}}$ ；

(2)、（ $\sqrt{3} + \sqrt{2}$ ）×（ $\sqrt{3} - \sqrt{2}$ ）

查看试题解析
20. 化简：

(1)、 $\frac{a^{2} - a b}{a^{2}} \div \frac{a^{2} - b^{2}}{a^{2} + 2 a b + b^{2}}$ ；

(2)、 $(\frac{1}{x - 2} - \frac{2}{x^{2} - 4 x + 4}) \times \frac{x - 2}{4 - x}$ ．

查看试题解析
21. 解方程：

(1)、 $\frac{1}{x - 2} + 3 = \frac{x - 1}{x - 2}$ ；

(2)、 $\frac{x + 1}{x - 1} - \frac{2}{x^{2} - 1} = 1$ ．

查看试题解析
22.
请在方格内画出△ABC，使它的顶点都在格点上，且三边长1， $\sqrt{2}$ ， $\sqrt{5}$ ，
①求△ABC的面积；②求出最长边上的高．

查看试题解析
23.
某校九年级（1）班所有学生参加2010年初中毕业生升学体育测试，根据测试评分标准，将他们的成绩进行统计后分为A、B、C、D四等，并绘制成如图所示的条形统计图和扇形统计图（未完成），请结合图中所给信息解答下列问题：

(1)、九年级（1）班参加体育测试的学生有人；

(2)、将条形统计图补充完整；

(3)、在扇形统计图中，等级B部分所占的百分比是，等级C对应的圆心角的度数为；

(4)、若该校九年级学生共有850人参加体育测试，估计达到A级和B级的学生共有多少人．

查看试题解析
24.
如图1，
李老师设计了一个探究杠杆平衡条件的实验：在一个自制类似天平的仪器的左边固定托盘A中放置一个重物，在右边活动托盘B（可左右移动）中放置一定质量的砝码，使得仪器左右平衡．改变活动托盘B与点O的距离x（cm），观察活动托盘B中砝码的质量y（g）的变化情况．实验数据记录如表：

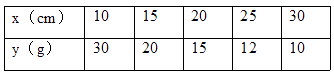(1)、把表中（x，y）的各组对应值作为点的坐标，在图2的坐标系中描出相应的点，用平滑曲线连接这些点；

(2)、观察所画的图象，猜测y与x之间的函数关系，求出函数关系式；

(3)、当砝码的质量为24g时，活动托盘B与点O的距离是多少？

查看试题解析
25. 果品店刚试营业，就在批发市场购买某种水果销售，第一次用500元购进若干千克水果，并以每千克定价7元出售，很快售完．由于水果畅销，第二次购买时，每千克的进价比第一次提高了20%，用660元所购买的数量比第一次多10千克．仍以原来的单价卖完．求第一次该种水果的进价是每千克多少元？

查看试题解析
26.
如图，在▱ABCD中，∠DAB=60°，点E、F分别在CD、AB的延长线上，且AE=AD，CF=CB．

(1)、求证：四边形AFCE是平行四边形；

(2)、若去掉已知条件的“∠DAB=60°”，上述的结论还成立吗？若成立，请写出证明过程；若不成立，请说明理由．

查看试题解析
27.
如图1，已知点A（﹣1，0），点B（0，﹣2），AD与y轴交于点E，且E为AD的中点，双曲线y= $\frac{k}{x}$ 经过C，D两点且D（a，4）、C（2，b）．

(1)、求a、b、k的值；

(2)、如图2，线段CD能通过旋转一定角度后点C、D的对应点C′、D′还能落在y= $\frac{k}{x}$ 的图象上吗？如果能，写出你是如何旋转的，如果不能，请说明理由；

(3)、如图3，点P在双曲线y= $\frac{k}{x}$ 上，点Q在y轴上，若以A、B、P、Q为顶点的四边形为平行四边形，试求满足要求的所有点P、Q的坐标．

查看试题解析