初中数学浙教版八年级下册第一章 二次根式 章末检测
试卷更新日期:2020-01-22 类型:单元试卷
一、单选题
-
1. 下列各式中,不是二次根式的是( )A、 B、- C、 D、2. 二次根式 的值是 ( )A、3 B、2 C、2 D、03. 若二次根式 在实数范围内有意义,则x的取值范围在数轴上表示正确的是( )A、
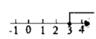 B、
B、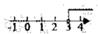 C、
C、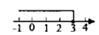 D、
D、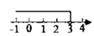 4. 在 、 、 中、 、 中,最简二次根式的个数有( )A、4 B、3 C、2 D、15. 若实数 满足 ,则 =( )A、2016 B、2017 C、4033 D、16. 下列实数中,有理数的是( )A、 B、 C、 D、π7. 实数a,b在数轴上的位置如图所示,则化简 的结果是( )
4. 在 、 、 中、 、 中,最简二次根式的个数有( )A、4 B、3 C、2 D、15. 若实数 满足 ,则 =( )A、2016 B、2017 C、4033 D、16. 下列实数中,有理数的是( )A、 B、 C、 D、π7. 实数a,b在数轴上的位置如图所示,则化简 的结果是( ) A、1 B、b+1 C、2a D、1-2a8. 已知 , ,则a,b的大小关系为( )A、a=b B、a<b C、a>b D、无法比较9. 下列二次根式中,可以与 合并的是( ).A、 B、 C、 D、10. 甲,乙两同学对代数式 (m>0,n>0)分别作了如下变形:
A、1 B、b+1 C、2a D、1-2a8. 已知 , ,则a,b的大小关系为( )A、a=b B、a<b C、a>b D、无法比较9. 下列二次根式中,可以与 合并的是( ).A、 B、 C、 D、10. 甲,乙两同学对代数式 (m>0,n>0)分别作了如下变形:甲: = = ;
乙: = = .
关于这两种变形过程的说法正确的是( )
A、甲,乙都正确 B、甲,乙都不正确 C、只有甲正确 D、只有乙正确二、填空题
-
11. 若 ,则 .12. 若 是正整数,则整数 的最小值为。13. 写出 的一个有理化因式.14. 若最简二次根式 与 能够合并,则a的值为。15. 如图,矩形内有两个相邻的正方形,面积分别为3和27,那么图中阴影部分的面积为。
 16. 阅读下列材料,我们知道( +3)( ﹣3)=4,因此将 的分子分母同时乘以“ +3”,分母就变成了4,即 = = ,从而可以达到对根式化简的目的.根据上述阅读材料解决问题:若m= ,则代数式m5+2m4﹣2017m3+2160的值是 .
16. 阅读下列材料,我们知道( +3)( ﹣3)=4,因此将 的分子分母同时乘以“ +3”,分母就变成了4,即 = = ,从而可以达到对根式化简的目的.根据上述阅读材料解决问题:若m= ,则代数式m5+2m4﹣2017m3+2160的值是 .三、解答题
-
17. 计算:(1)、(2)、 × - .(3)、(4)、18. 已知x= ( + ),y= ( - ),求下列各式的值:(1)、x2-xy+y2;(2)、 + .19. 先化简,再求值.
,其中
20. 站在水平高度为h米的地方看到可见的水平距离为d米,它们符合公式为 。某一登山者从海拔h米处登上海拔2h米高的山顶,那么他看到的水平线的距离是原来的多少倍?21. 已知:如图,Rt△ABC中,∠C=90°,AC= ,BC= ,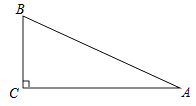
求:
(1)、Rt△ABC的面积;(2)、斜边AB的长.22. 拦河坝的横断面是梯形,如图,其上底是 m,下底是 m,高是 m. (1)、求横断面的面积;(2)、若用300 m3的土,可修多长的拦河坝?
(1)、求横断面的面积;(2)、若用300 m3的土,可修多长的拦河坝?
