初中数学浙教版七年级下册第二章 二元一次方程组 章末检测
试卷更新日期:2020-01-21 类型:单元试卷
一、单选题
-
1. 下列各式是二元一次方程的是 ( )A、 B、 C、 D、2. 下列方程组是二元一次方程组的是( )A、
 B、
B、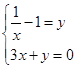 C、
C、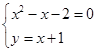 D、
D、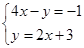 3. 判断下列四组x,y的值,是二元一次方程2x﹣y=﹣4的解的是( )A、 B、 C、 D、4. 若关于x,y的二元一次方程组 有整数解,则满足要求的所有整数a的个数为( )A、0 B、4 C、8 D、125. 关于 x 的代数式ax+b,当 x 取值分别为-1,0,1,2 时,对应的代数式的值如下表( )
3. 判断下列四组x,y的值,是二元一次方程2x﹣y=﹣4的解的是( )A、 B、 C、 D、4. 若关于x,y的二元一次方程组 有整数解,则满足要求的所有整数a的个数为( )A、0 B、4 C、8 D、125. 关于 x 的代数式ax+b,当 x 取值分别为-1,0,1,2 时,对应的代数式的值如下表( )x
···
-1
0
1
2
···
y
···
-2
1
4
7
···
则 a+b 的值是( )
A、-2 B、1 C、4 D、76. 方程组 的解为( ).A、 B、 C、 D、7. 如图,由七个完全一样的小长方形组成的大长方形ABCD, CD=7,长方形ABCD的周长为( ) A、32 B、33 C、34 D、358. 我国古代《四元玉鉴》中记载“二果问价”问题,其内容如下:九百九十九文钱,甜果苦果买一千,甜果九个十一文,苦果七个四文钱,试问甜苦果几个,又问各该几个钱?若设买甜果x个,买苦果y个,则下列关于x,y的二元一次方程组中符合题意的是( )A、 B、 C、 D、9. 现用186张铁皮做盒子,每张铁皮可做8个盒身或15个盒底,且一个盒身与两个盒底配成一个盒子.设用 张铁皮做盒身, 张铁皮做盒底,则可得方程组( )A、 B、 C、 D、10. 如果 ,其中xyz≠0,那么x:y:z=( )
A、32 B、33 C、34 D、358. 我国古代《四元玉鉴》中记载“二果问价”问题,其内容如下:九百九十九文钱,甜果苦果买一千,甜果九个十一文,苦果七个四文钱,试问甜苦果几个,又问各该几个钱?若设买甜果x个,买苦果y个,则下列关于x,y的二元一次方程组中符合题意的是( )A、 B、 C、 D、9. 现用186张铁皮做盒子,每张铁皮可做8个盒身或15个盒底,且一个盒身与两个盒底配成一个盒子.设用 张铁皮做盒身, 张铁皮做盒底,则可得方程组( )A、 B、 C、 D、10. 如果 ,其中xyz≠0,那么x:y:z=( )
A、1:2:3 B、2:3:4 C、2:3:1 D、3:2:1二、填空题
-
11. 方程 是二元一次方程,则 =.12. 小亮解方程组 的解为 ,由于不小心,滴上了两滴墨水,刚好遮住了两个数●和★,请你帮他找回★这个数★=.13. 已知 ,则 x= , y= .
14. 某学校有两种类型的学生宿舍30间,大宿舍每间可以住8人,小宿舍每间可以住5人,该学校共有198个住宿生,恰好可以住满这30间宿舍,若设大宿舍x间,小宿舍y间,则可以列出的方程组为:。15. 2017年,随州学子尤东梅参加《最强大脑》节目,成功完成了高难度的项目挑战,展现了惊人的记忆力.在2019年的《最强大脑》节目中,也有很多具有挑战性的比赛项目,其中《幻圆》这个项目充分体现了数学的魅力.如图是一个最简单的二阶幻圆的模型,要求:①内、外两个圆周上的四个数字之和相等;②外圆两直径上的四个数字之和相等,则图中两空白圆圈内应填写的数字从左到右依次为和. 16. A , B , C三种大米的售价分别为40元、50元、70元,其中B , C两种大米的进价为40元、50元,经核算,三种大米的总利润相同,且A , B两种大米的销售量之和是C种大米之和的6倍,则A种大米的进价是 .
16. A , B , C三种大米的售价分别为40元、50元、70元,其中B , C两种大米的进价为40元、50元,经核算,三种大米的总利润相同,且A , B两种大米的销售量之和是C种大米之和的6倍,则A种大米的进价是 .三、计算题
-
17. 解下列方程组:(1)、(2)、18. 课本里,用代入法解二元一次方程组 的过程是用下面的框图表示:
根据以上思路,请用代入法求出方程组 的解(不用画框架图).
 19. 已知关于x , y的二元一次方程组 的解适合方程x+y=6,求n的值.20. 根据下图提供的信息,求每件 恤衫和每瓶矿泉水的价格.
19. 已知关于x , y的二元一次方程组 的解适合方程x+y=6,求n的值.20. 根据下图提供的信息,求每件 恤衫和每瓶矿泉水的价格.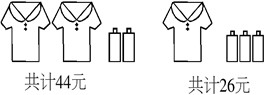 21. 茜茜受《乌鸦喝水》故事的启发,利用量筒、大球和小球进行了如下操作,请根据图中给出的信息,解答下列问题:
21. 茜茜受《乌鸦喝水》故事的启发,利用量筒、大球和小球进行了如下操作,请根据图中给出的信息,解答下列问题: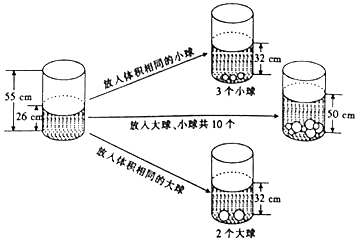 (1)、放入一个小球水面升高cm,放入一个大球水面升高cm.(2)、如果要使水面上升到50cm,应放入大球、小球各多少个?22. 育新中学组织20个团员分成两组分别去A,B两地开展植树活动,去A地植树人数不超过10人时,每人能植树6棵,去A地植树人数超过10人时,每人只能植树4棵.在B池的团员每人植树5棵。(每个团员所植树的棵数均满足要求)(1)、若这批团员中,去A地的人数超过10人,本次植树活动共植树86棵。问去A,B两地团员各多少人?(2)、小明同学说“经统计,本次我们20个团员共植树96棵”,你认为小明同学的统计有问题吗?请你通过计算说明.(3)、当去A,B闭地的团炎到达目的地后,B地团员发现还有8位大人义工也来植树,在B地原来团员同学每人可以植树5棵,大人每人植树10标,如果抽取一部分大人协助指导团员植树,这样B组团员每人可以植树8棵,被抽取的大人每人只能植树5棵;就团员和大人在B地的植树的总数来看。有大人协助比没有大人协助多了15棵,求到B地的团员人数。23. 一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
(1)、放入一个小球水面升高cm,放入一个大球水面升高cm.(2)、如果要使水面上升到50cm,应放入大球、小球各多少个?22. 育新中学组织20个团员分成两组分别去A,B两地开展植树活动,去A地植树人数不超过10人时,每人能植树6棵,去A地植树人数超过10人时,每人只能植树4棵.在B池的团员每人植树5棵。(每个团员所植树的棵数均满足要求)(1)、若这批团员中,去A地的人数超过10人,本次植树活动共植树86棵。问去A,B两地团员各多少人?(2)、小明同学说“经统计,本次我们20个团员共植树96棵”,你认为小明同学的统计有问题吗?请你通过计算说明.(3)、当去A,B闭地的团炎到达目的地后,B地团员发现还有8位大人义工也来植树,在B地原来团员同学每人可以植树5棵,大人每人植树10标,如果抽取一部分大人协助指导团员植树,这样B组团员每人可以植树8棵,被抽取的大人每人只能植树5棵;就团员和大人在B地的植树的总数来看。有大人协助比没有大人协助多了15棵,求到B地的团员人数。23. 一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)车型
甲
乙
丙
汽车运载量(吨/辆)
5
8
10
汽车运费(元/辆)
400
500
600
(1)、若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?(2)、为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?(3)、求出那种方案的运费最省?最省是多少元.