浙江省宁波市六校联考2019-2020学年高二上学期数学期中考试试卷
试卷更新日期:2020-01-16 类型:期中考试
一、单选题
-
1. 空间中一点 到平面 的距离为( )A、2 B、3 C、1 D、2. 若点 到直线 的距离为4,且在不等式 表示的平面区域内,则点 的横坐标是( )A、7或-3 B、7 C、-3 D、-7或33. 设 , 是两条不同的直线, , 是两个不同的平面,是下列命题正确的是( )A、若 , ,则 B、若 , , ,则 C、若 , , ,则 D、若 , , ,则4. 在平面直角坐标系中, 为不等式组 所表示的区域上一动点,则 的最小值为( )A、2 B、1 C、 D、5. 已知直线 与 平行,则 等于( )A、 或 B、 或 C、 D、6. 长方体 中, , 为 中点,则异面直线 与 所成角为( )A、 B、 C、 D、7. 已知点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系是( )A、相切 B、相交 C、相离 D、不确定8. 已知直线 : 与曲线 有两个公共点,则实数 的取值范围是( )A、 B、 C、 D、9. 如图,在正四棱锥S-ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:①EP⊥AC;②EP∥BD;③EP∥平面SBD;④EP⊥平面SAC,其中恒成立的为( )
 A、①③ B、③④ C、①② D、②③④10. 若圆 上至少有三个不同的点到直线 的距离为 ,则直线 的倾斜角的取值范围是( )A、 B、 C、 D、
A、①③ B、③④ C、①② D、②③④10. 若圆 上至少有三个不同的点到直线 的距离为 ,则直线 的倾斜角的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 直线 的斜率为;倾斜角的大小是 .12. 已知 ,若方程 表示圆,则圆心坐标为; 的取值范围是 .13. 《九章算术》中的“邪田”意为直角梯形,上、下底称为畔,高称为正广,非高腰边称为邪。在四棱锥 中,底面 为邪田,两畔 分别为1,3,正广 为 , 平面 ,则邪田 的邪长为;邪所在直线与平面 所成角的大小为.14. 直线 被圆 : 所截得的弦长为;由直线 上的一点向圆 引切线,切线长的最小值为.15. 已知 , , 满足约束条件 ,若 的最小值为-1,则 .16. 如图所示,有一条长度为1的线段 ,其端点 , 在边长为4的正方形 的四边上滑动,当点 绕着正方形的四边滑动一周时, 的中点 所形成的轨迹长度为.
 17. 在 中,已知 , , , 是边 上一点,将 沿 折起,得到三棱锥 。若该三棱锥的顶点 在底面 的射影 在线段 上,设 ,则 的取值范围为.
17. 在 中,已知 , , , 是边 上一点,将 沿 折起,得到三棱锥 。若该三棱锥的顶点 在底面 的射影 在线段 上,设 ,则 的取值范围为.三、解答题
-
18. 已知平面内两点A(8,-6),B(2,2).(1)、求过点P(2,-3)且与直线AB平行的直线l的方程;
(2)、一束光线从B点射向(1)中直线l,若反射光线过点A,求反射光线所在的直线方程.19. 如图,在四棱锥 中, 平面 , , , , . 为线段 的中点.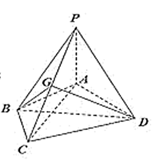 (1)、证明: 面 ;(2)、求 与平面 所成的角的正弦值.20. 已知圆 : ,直线 过定点 .(1)、若 与圆 相切,求 的方程;(2)、若 与圆 相交于 , 两点,求三角形 面积的最大值,并求此时 的直线方程.21. 如图所示的几何体中, 垂直于梯形 所在的平面, 为 的中点, ,四边形 为矩形,线段 交 于点 .
(1)、证明: 面 ;(2)、求 与平面 所成的角的正弦值.20. 已知圆 : ,直线 过定点 .(1)、若 与圆 相切,求 的方程;(2)、若 与圆 相交于 , 两点,求三角形 面积的最大值,并求此时 的直线方程.21. 如图所示的几何体中, 垂直于梯形 所在的平面, 为 的中点, ,四边形 为矩形,线段 交 于点 . (1)、求证: 平面 ;(2)、求二面角 的正弦值;(3)、在线段 上是否存在一点 ,使得 与平面 所成角的大小为 ?若存在,求出 的长;若不存在,请说明理由.22. 若圆 经过坐标原点和点 ,且与直线 相切, 从圆 外一点 向该圆引切线 , 为切点,
(1)、求证: 平面 ;(2)、求二面角 的正弦值;(3)、在线段 上是否存在一点 ,使得 与平面 所成角的大小为 ?若存在,求出 的长;若不存在,请说明理由.22. 若圆 经过坐标原点和点 ,且与直线 相切, 从圆 外一点 向该圆引切线 , 为切点,(Ⅰ)求圆 的方程;
(Ⅱ)已知点 ,且 , 试判断点 是否总在某一定直线 上,若是,求出 的方程;若不是,请说明理由;
(Ⅲ)若(Ⅱ)中直线 与 轴的交点为 ,点 是直线 上两动点,且以 为直径的圆 过点 ,圆 是否过定点?证明你的结论.