天津市南开区2019-2020学年高一上学期数学期末考试试卷

试卷更新日期：2020-01-16 类型：期末考试

进入出卷网下载

一、单选题

1. 设全集 $U = {1, 2, 3, 4}$ ，集合 $S = {1, 2}$ ， $T = {2, 3}$ ，则 $(∁_{U} S) \cap T$ 等于（）

A、 ${2}$ B、 ${3}$ C、 ${4}$ D、 ${2, 3, 4}$

查看试题解析
2. 命题“ $\exists x_{0} \in (0, + \infty), \ln x_{0} = x_{0} - 1$ ”的否定是（）

A、 $\exists x_{0} \in (0, + \infty), \ln x_{0} \neq x_{0} - 1$ B、 $\exists x_{0} \notin (0, + \infty), \ln x_{0} = x_{0} - 1$ C、 $\forall x \in (0, + \infty), \ln x \neq x - 1$ D、 $\forall x \notin (0, + \infty), \ln x = x - 1$

查看试题解析
3. 下列函数中为偶函数，且在 $(0, + \infty)$ 上单调递增的是（）

A、 $y = \lg (2 x)$ B、 $y = - x^{2}$ C、 $y = 2^{x}$ D、 $y = \sqrt{| x |}$

查看试题解析
4. “ $\frac{1}{a} < \frac{1}{b}$ ”是“ $b < a < 0$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
5. $\cos 480^{\circ}$ 等于（）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、 $- \frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
6. 设 $a = \log_{0.5} 6$ ， $b = {0.5}^{6}$ ， $c = 6^{0.5}$ ，则 $a$ 、 $b$ 、 $c$ 的大小顺序是（）

A、 $b < a < c$ B、 $b < c < a$ C、 $a < c < b$ D、 $a < b < c$

查看试题解析
7. 为了得到函数 $y = \sin (2 x - \frac{π}{6})$ 的图象，只需把函数 $y = \sin (2 x + \frac{π}{3})$ 的图象（）

A、向左平移 $\frac{π}{12}$ 个单位长度 B、向右平移 $\frac{π}{4}$ 个单位长度 C、向左平移 $\frac{π}{6}$ 个单位长度 D、向右平移 $\frac{π}{2}$ 个单位长度

查看试题解析
8. 如图 $1$ 是某条公共汽车线路收支差额 $y$ 与乘客量 $x$ 的图象（收支差额 $=$ 车票收入 $-$ 支出费用）．由于目前本条线路亏损，公司有关人员将图 $1$ 变为图 $2$ 与图 $3$ ，从而提出了扭亏为盈的两种建议．下面有 $4$ 种说法：

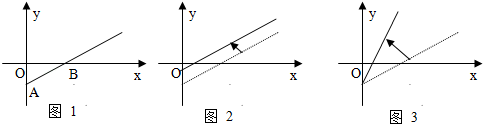
⑴图 $2$ 的建议是：减少支出，提高票价；（2）图 $2$ 的建议是：减少支出，票价不变；（3）图 $3$ 的建议是：减少支出，提高票价；（4）图 $3$ 的建议是：支出不变，提高票价；上面说法中正确的是（）

A、（1）（3） B、（1）（4） C、（2）（4） D、（2）（3）

查看试题解析
9. 已知三个函数 $f (x) = 2^{x} + x - 2$ ， $g (x) = x^{3} - 8$ ， $h (x) = \log_{2} x + x - 2$ 的零点依次为 $a$ 、 $b$ 、 $c$ ，则 $a + b + c =$ （）

A、 $6$ B、 $5$ C、 $4$ D、 $3$

查看试题解析
10. 若一系列的函数解析式相同，值域相同但定义域不同，则称这些函数为“孪生函数”．那么函数解析式为y=2x²+1，值域为{3，19}的“孪生函数”共有（　　）

A、15个 B、12个 C、9个 D、8个

查看试题解析

二、填空题

11. 已知幂函数 $y = f (x)$ 的图象过点 $(2, \frac{\sqrt{2}}{2})$ ，则 $f (x) =$ ．

查看试题解析
12. 设 $x \in R$ ，使不等式 $14 - 4 x^{2} \geq x$ 成立的 $x$ 的取值范围为.

查看试题解析
13. 若函数 $f (x) = {\begin{array}{l} (a - 1) x - 2 a, x \leq 1 \\ \log_{\frac{1}{3}} x, x > 1 \end{array}$ 的值域是 $R$ ，则实数 $a$ 的取值范围是．

查看试题解析
14. △ABC中， $sin A = \frac{3}{5}$ ， $cos B = \frac{5}{13}$ ，则 $cos C$ = ．

查看试题解析
15. 已知 $a > 0$ ， $b > 0$ ，且 $a + b = 8$ ，则 $\frac{3 a b}{a + 4 b}$ 的最大值是．

查看试题解析

三、解答题

16. 求值：

(1)、 ${(\frac{16}{81})}^{- \frac{3}{4}} - 2 e^{0} + \ln 1 - \lg 4 + \lg 5^{- 2} + \log_{3} 5 \times \log_{5} 9$ ；

(2)、已知 $a > 0$ ， $a^{2 x} = 3$ ，求 $\frac{a^{3 x} + a^{- 3 x}}{a^{x} + a^{- x}}$ 的值．

查看试题解析
17. 已知 $f (x)$ 是定义在 $R$ 上的奇函数，且 $x \in (0, + \infty)$ 时， $f (x) = {\begin{array}{l} 7 - 2 | x - 1|, 0 < x \leq 2 \\ x + \frac{9}{x}, x > 2 \end{array}$ .

(1)、求 $f (0)$ ， $f (f (- 2))$ 的值；

(2)、若 $f (a) = 6$ ，求 $a$ 的值．

查看试题解析
18. 如图，在平面直角坐标系 $x O y$ 中，以 $O x$ 轴为始边作两个锐角 $α$ 、 $β$ ，它们的终边分别与单位圆相交于 $A$ 、 $B$ 两点，已知 $A$ 、 $B$ 的横坐标分别为 $\frac{2 \sqrt{5}}{5}$ 、 $\frac{\sqrt{2}}{10}$ ．

(1)、求 $\tan 2 α$ 的值；

(2)、求 $2 α + β$ 的值．

查看试题解析
19. 已知函数 $f (x) = 2 \cos x (\sin x - \sqrt{3} \cos x) + \sqrt{3}$ ．

(1)、求 $f (x)$ 的最小正周期和对称中心；

(2)、求 $f (x)$ 的单调递减区间；

(3)、当 $x \in [\frac{π}{2} ， π]$ 时，求函数 $f (x)$ 的最小值及取得最小值时 $x$ 的值．

查看试题解析
20. 已知二次函数 $f (x) = a x^{2} + b x + c (a, b, c \in R)$ ， $f (- 2) = f (0) = 0$ ， $f (x)$ 的最小值为 $- 1$ ．

(1)、求函数 $f (x)$ 的解析式；

(2)、设 $g (x) = f (- x) - λ f (x) + 1$ .
（i）若 $g (x)$ 在 $[- 1, 1]$ 上是减函数，求实数 $λ$ 的取值范围；

（ii）若 $g (x)$ 在 $(- 1, 1)$ 内恰有一个零点，求实数 $λ$ 的取值范围．

查看试题解析