北京市海淀区2019-2020学年高三上学期数学期末试卷
试卷更新日期:2020-01-16 类型:期末考试
一、单选题
-
1. 已知集合 , , ,则集合 是( )A、 B、 C、 D、2. 抛物线 的焦点坐标为( )A、 B、 C、 D、3. 下列直线与圆 相切的是( )A、 B、 C、 D、4. 已知 、 ,且 ,则( )A、 B、 C、 D、5. 在 的展开式中, 的系数为( )A、 B、 C、 D、6. 已知平面向量 、 、 满足 ,且 ,则 的值为( )A、 B、 C、 D、7. 已知 、 、 是三个不同的平面,且 , ,则“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件8. 已知等边 边长为 ,点 在 边上,且 , .下列结论中错误的是( )A、 B、 C、 D、9. 声音的等级 (单位: )与声音强度 (单位: )满足 . 喷气式飞机起飞时,声音的等级约为 ;一般说话时,声音的等级约为 ,那么喷气式飞机起飞时声音强度约为一般说话时声音强度的( )A、 倍 B、 倍 C、 倍 D、 倍10. 若点 为点 在平面 上的正投影,则记 .如图,在棱长为 的正方体 中,记平面 为 ,平面 为 ,点 是棱 上一动点(与 、 不重合) , .给出下列三个结论:

①线段 长度的取值范围是 ;②存在点 使得 平面 ;③存在点 使得 .其中,所有正确结论的序号是( )
A、①②③ B、②③ C、①③ D、①②二、填空题
-
11. 在等差数列 中,若 ,则 .12. 若复数 ,则 .13. 已知点 ,点 、 分别为双曲线 的左、右顶点.若 为正三角形,则该双曲线的离心率为.14. 已知函数 在区间 上存在最小值,则实数 的取值范围是.15. 用“五点法”作函数 的图象时,列表如下:
则 , .
16. 已知曲线 ( 为常数).(i)给出下列结论:
①曲线 为中心对称图形;
②曲线 为轴对称图形;
③当 时,若点 在曲线 上,则 或 .
其中,所有正确结论的序号是.
(ii)当 时,若曲线 所围成的区域的面积小于 ,则 的值可以是.(写出一个即可)
三、解答题
-
17. 已知函数 .
(Ⅰ)求函数 的单调递增区间;
(Ⅱ)若 在区间 上的最大值为 ,求 的最小值.
18. 如图,在三棱锥 中,平面 平面 , 和 均是等腰直角三角形, , , 、 分别为 、 的中点.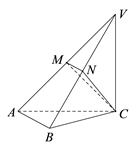
(Ⅰ)求证: 平面 ;
(Ⅱ)求证: ;
(Ⅲ)求直线 与平面 所成角的正弦值.
19. 某市《城市总体规划( 年)》提出到 年实现“ 分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身 个方面构建“ 分钟社区生活圈”指标体系,并依据“ 分钟社区生活圈”指数高低将小区划分为:优质小区(指数为 )、良好小区(指数为 )、中等小区(指数为 )以及待改进小区(指数为 ) 个等级.下面是三个小区 个方面指标的调查数据:
注:每个小区“ 分钟社区生活圈”指数 ,其中 、 、 、 为该小区四个方面的权重, 、 、 、 为该小区四个方面的指标值(小区每一个方面的指标值为 之间的一个数值).
现有 个小区的“ 分钟社区生活圈”指数数据,整理得到如下频数分布表:
分组
频数
(Ⅰ)分别判断 、 、 三个小区是否是优质小区,并说明理由;
(Ⅱ)对这 个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取 个小区进行调查,若在抽取的 个小区中再随机地选取 个小区做深入调查,记这 个小区中为优质小区的个数为 ,求 的分布列及数学期望.
20. 已知椭圆 的右顶点 ,且离心率为 .(Ⅰ)求椭圆 的方程;
(Ⅱ)设 为原点,过点 的直线 与椭圆 交于两点 、 ,直线 和 分别与直线 交于点 、 ,求 与 面积之和的最小值.