江苏省苏州市2019-2020学年八年级上学期数学期末考试考试卷
试卷更新日期：2020-01-15 类型：期末考试
一、选择题(本大题共10小题每小题2分，共20分)
-
1. 下列四个图标中，轴对称图案为（ ）A、
B、
C、
D、
2. 等于（ ）A、4 B、-4 C、±4 D、±23. 在平面直角坐标系中，点(2，-5)关于y轴对称的点的坐标为（ ）A、(2，5) B、(-2，-5) C、(2，-5) D、(-2，5)4. 若点P在一次函数y=-4x+2的图像上，则点P一定不在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列整数中，与2- 最接近的是（ ）A、-1 B、0 C、1 D、26. 在△ABC中，∠A，∠B，∠C的对边分别是a、b、c，下列条件中，能判断△ABC是直角三角形（ ）A、a=2，b=3，c=4 B、a：b：c= C、∠A+∠B=2∠C D、∠A=2∠B=3∠C7. 如图，在△ABC中，AB=AC，AD为BC边上的高，点E为AC的中点，连接DE，若△ABC的周长为20，则△CDE的周长为（ ）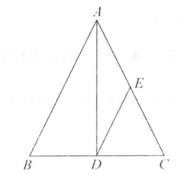
A、10 B、12 C、14 D、168. 如图，BD是△ABC的角平分线，DE⊥AB，垂足为E，AB=6，BC=4，DE=2，则△ABC的面积为（ ）
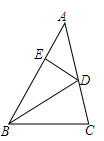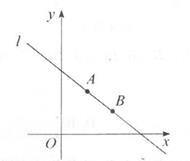
A、4 B、6 C、8 D、109. 如图，一次函数y= x+6的图像与x轴、y轴分别交于点A，B，过点B的直线l平分△ABO的面积，则直线l相应的函数表达式为（ ）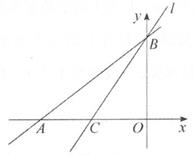
A、y= x+6 B、y= x+6 C、y= x+6 D、y= x+610. 在如图所示的正方形网格中，已知小正方形的边长为1，△ABC与△DEF的顶点均为格点，边AC、DF交于点G．下面有四个结论：①△ABC≌△DEF；②图中阴影部分(即△ABC与△DEF重叠部分)的面积为1.5；③△DCG为等边三角形；④AG=DG．其中结论正确的个数为（ ）
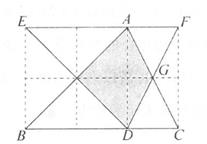A、1个 B、2个 C、3个 D、4个二、填空题(本大题共8小题，每小题2分，共16分)
-
11. 比较大小： 1。(填“>”、“=”或“<”)12. 下列5个数：0.13113、 、π、0、 ，其中无理数有个。(填具体数字)13. 如图，已知点A(x1 ， y1)、B(x2 ， y2)在一次函数y=kx+b(k<0)的图像上，则y1y2。(填“>”或“<”)
14. 如图，在△ABC中，D为边BC上一点，AB=BD。若∠B=40°，∠C=36°，则∠DAC°。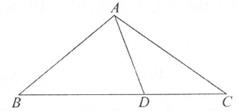
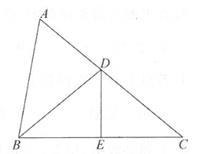
15. 一次函数y= x+3的图像与x轴、y轴围成的三角形面积为。16. 若点A(m，n)在一次函数y=2x+b的图像上，且2m-n>1，则b的取值范围为。17. 如图，将有一边重合的两张直角三角形纸片放在数轴上，纸片上的点A表示的数是-2，AC=BC=BD=1。若以点A为圆心、AD的长为半径画弧，与数轴交于点E(点E位于点A右侧)，则点E表示的数为 。
18. 如图，在△ABC中，AD为BC边上的中线，延长AD到点E，使得DE=AD，连接BE。若AB=5，AC=3，AD=2，则△ABC的面积为。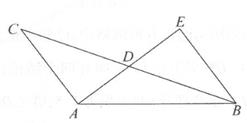
三、解答题(本大题共10小题，共64分．)
-
19. 计算：(π-1)0- +( )220. 某科技公司在2019年第三季度共售出约65 700 000部智能手机，占全球市场份额18%。(1)、2019年第三季度全球市场共售出智能手机部；(2)、用四舍五入法将(1)中计算得到的数据精确到10 000 000，并用科学记数法表示。21. 如图，在△ABC中，∠A=60°，∠ABC=2∠C，BC边的垂直平分线交AC边于点D，交BC边于点E，连接BD，求∠ADB的度数。
22. 如图，在正方形网格中，每个小正方形的边长均为1，△ABC三个顶点都在格点上。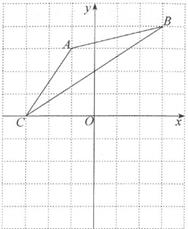
(1)、画出△ABC关于x轴对称的△A'B'C；(2)、连接AB'，判断△AB'C的形状，并说明理由。23. 某长途客运公司规定旅客可免费携带一定质量的行李，当行李的质量超过规定时，需支付相应的行李费。设x表示行李的质量(kg)，y表示行李费(元)，y与x的函数关系如图所示，请写出x、y变化过程中的实际意义。
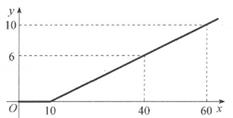24. 如图，在平面直角坐标系中，一次函数y=kx+3的图像与x轴y轴分别交于点A、B，点A的坐标为(2，0)。
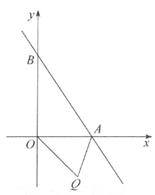(1)、求k的值；(2)、已知点Q在第四象限，且到两坐标轴距离相等，若△AOB的面积是△AOQ面积的2倍，求点Q的坐标。25. 如图，AB=AD，AC=AE，∠BAD=∠CAE，点E在BC上，AB、DE相交于点F。
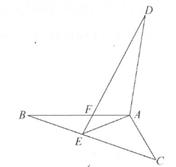(1)、求证：△ABC≌△ADE；(2)、求证：∠BEF=∠CAE。26. 如图，△BCE、△ACD分别是以BE、AD为斜边的直角三角形，BE=AD，△CDE是等边三角形。
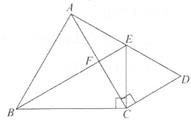(1)、求证：BE⊥AC；(2)、若AD=6，求BF的长。27. 如图①所示，甲、乙两车从A地出发，沿相同路线前往同一目的地，途中经过B地。甲车先出发，当甲车到达B地时，乙车开始出发，当乙车到达B地时，甲车与B地相距 km设甲、乙两车与B地之间的距离为y1(km)、y2(km)，乙车行驶的时间为x(h)，y1、y2与x的函数关系如图②所示
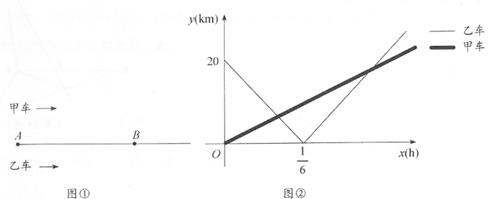(1)、A、B两地之间的距离为km；(2)、当x为何值时，甲、乙两车相距5km?28. 在平面直角坐标系中，直线y=x+2与x轴、y轴分别交于点A、B，点D的坐标为(0，3)，点E是线段AB上的一点，以DE为腰在第二象限内作等腰直角△DEF，∠EDF=90°。
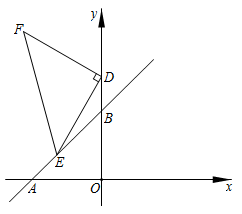(1)、请直接写出点A、B的坐标：A( ， )、B（ ， ）；(2)、设点F的坐标为(a，b)，连接FB并延长交x轴于点G，求点G的坐标。