云南省红河州泸西县2019年数学中考一模试卷
试卷更新日期:2020-01-15 类型:中考模拟
一、单选题
-
1. 我国自行设计、自主集成研制的蛟龙号载人潜水器最大下潜深度为7062m.将7062用科学记数法表示为( )A、7.062×103 B、7.1×103 C、0.7062×104 D、7.062×1042. 函数y= 中,自变量x的取值范围是( )A、x≥1 B、x>1 C、x≥1且x≠2 D、x≠23. 下列图形是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图),则这个几何体是( )
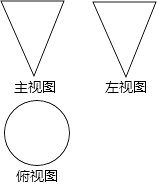 A、三棱柱 B、三棱锥 C、圆柱 D、圆锥4. 下列计算正确的是( )A、a2•a3=a6 B、(﹣2a)3=﹣6a3 C、 D、(3.14﹣π)0=05. 如果一个多边形的内角和是1800°,这个多边形是( )A、八边形 B、十四边形 C、十边形 D、十二边形6. 关于x的一元二次方程x2+3x﹣1=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定7. 按一定规律排列的实数:﹣1, ,﹣ , ,- …,第n个实数是( )A、 B、- C、(﹣n)n+1 D、(﹣1)n8. 在正方形网格中△ABC的位置如图所示,则cos∠B的值为( )
A、三棱柱 B、三棱锥 C、圆柱 D、圆锥4. 下列计算正确的是( )A、a2•a3=a6 B、(﹣2a)3=﹣6a3 C、 D、(3.14﹣π)0=05. 如果一个多边形的内角和是1800°,这个多边形是( )A、八边形 B、十四边形 C、十边形 D、十二边形6. 关于x的一元二次方程x2+3x﹣1=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定7. 按一定规律排列的实数:﹣1, ,﹣ , ,- …,第n个实数是( )A、 B、- C、(﹣n)n+1 D、(﹣1)n8. 在正方形网格中△ABC的位置如图所示,则cos∠B的值为( )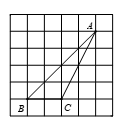 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. ﹣4的绝对值是 .10. 分解因式:a3﹣a= .11. 在△ABC中,E、F分别为AB,AC的中点,则△AEF与△ABC的面积之比为.12. 2018年国家将扩大公共场所免费上网范围,某小区响应号召调查小区居民上网费用情况,随机抽查了30户家庭的月上网费用,结果如表
月网费(元)
50
100
150
户数(人)
15
12
3
则关于这30户家庭的月上网费用,中位数是.
13. 如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=40°,则∠AED=. 14. 如图,直线l⊥x轴于点P,且与反比例函数y1= (x>0)及y2= (x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1﹣k2=.
14. 如图,直线l⊥x轴于点P,且与反比例函数y1= (x>0)及y2= (x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1﹣k2=.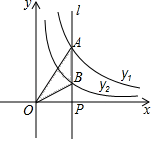
三、解答题
-
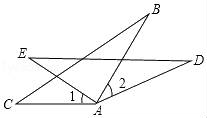
15. 先化简,再求值:(1﹣ )× ,其中a= .16. 如图所示,AC=AE,∠1=∠2,AB=AD.求证:BC=DE.
 17. 某中学开展“我的中国梦﹣﹣青春励志篇”活动,开设了A:美术活动社,B:音乐活动社,C:科技活动社,D:体育活动社四种活动社,为了解学生对四种活动社的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图 两个统计图,请结合图中信息解答问题:
17. 某中学开展“我的中国梦﹣﹣青春励志篇”活动,开设了A:美术活动社,B:音乐活动社,C:科技活动社,D:体育活动社四种活动社,为了解学生对四种活动社的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图 两个统计图,请结合图中信息解答问题: (1)、在这项调查中,共调查了多少名学生?(2)、请将两个统计图补充完整.(3)、若该校有1200名学生,请估计喜欢体育活动社的学生大约有多少名?18. 党的十九大提出,建设生态文明是中华民族永续发展的千年大计,某同学参加“加强生态环境保护,建设美丽中国”手工大赛,他用一种环保材料制作A、B两种手工艺品,制作1件A种手工艺品和3件B种手工艺品需要环保材料5米,制作4件A种手工艺品和5件B种手工艺品需要环保材料13米,求制作一件A种手工艺品和1件B种手工艺品各需多少米环保材料?19. 一只不透明袋子中装有三只大小、质地都相同的小球,球面上分别标有数字1、﹣2、3,搅匀后先从中任意摸出一个小球(不放回),记下数字作为点A的横坐标,再从余下的两个小球中任意摸出一个小球,记下数字作为点A的纵坐标.(1)、用画树状图或列表等方法列出所有可能出现的结果;(2)、求点A落在第四象限的概率.20. A市和B市分别有某种库存机器12台和6台,现决定支援C村10台,D村8台,已知从A市调运一台机器到C村和D村的运费分别是400元和800元,从B市调运一台机器到C村和D村的运费分别是300元和500元.(1)、设B市运往C村机器x台,求总运费W关于x的函数关系式;(2)、若要求总运费不超过9000元,共有几种调运方案?(3)、求出总运费最低的调运方案,最低运费是多少元?
(1)、在这项调查中,共调查了多少名学生?(2)、请将两个统计图补充完整.(3)、若该校有1200名学生,请估计喜欢体育活动社的学生大约有多少名?18. 党的十九大提出,建设生态文明是中华民族永续发展的千年大计,某同学参加“加强生态环境保护,建设美丽中国”手工大赛,他用一种环保材料制作A、B两种手工艺品,制作1件A种手工艺品和3件B种手工艺品需要环保材料5米,制作4件A种手工艺品和5件B种手工艺品需要环保材料13米,求制作一件A种手工艺品和1件B种手工艺品各需多少米环保材料?19. 一只不透明袋子中装有三只大小、质地都相同的小球,球面上分别标有数字1、﹣2、3,搅匀后先从中任意摸出一个小球(不放回),记下数字作为点A的横坐标,再从余下的两个小球中任意摸出一个小球,记下数字作为点A的纵坐标.(1)、用画树状图或列表等方法列出所有可能出现的结果;(2)、求点A落在第四象限的概率.20. A市和B市分别有某种库存机器12台和6台,现决定支援C村10台,D村8台,已知从A市调运一台机器到C村和D村的运费分别是400元和800元,从B市调运一台机器到C村和D村的运费分别是300元和500元.(1)、设B市运往C村机器x台,求总运费W关于x的函数关系式;(2)、若要求总运费不超过9000元,共有几种调运方案?(3)、求出总运费最低的调运方案,最低运费是多少元?分析由已知条件填出下表:
库存机器
支援C村
支援D村
B市
6台
x台
(6﹣x)台
A市
12台
(10﹣x)台
[8﹣(6﹣x)]台
21. 如图,抛物线y=﹣x2+5x+n经过点A(1,0),与y轴交于点B. (1)、求抛物线的解析式;(2)、P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标.
(1)、求抛物线的解析式;(2)、P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标.