新疆乌鲁木齐市高新区(新市区)2019届数学中考一模试卷
试卷更新日期:2020-01-15 类型:中考模拟
一、单选题
-
1. 如果把收入100元记作+100元,那么支出80元记作( )A、+20元 B、+100元 C、+80元 D、-80元2. 如图,已知a∥b,l与a、b相交,若∠1=70°,则∠2的度数等于( )
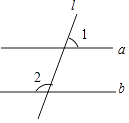 A、120° B、110° C、100° D、70°3. 下列计算正确的是( )A、2x+3y=5xy B、(﹣2x2)3=﹣6x6 C、3y2•(﹣y)=﹣3y2 D、6y2÷2y=3y4. 如图,是某几何体的三视图,则这个几何体是( )
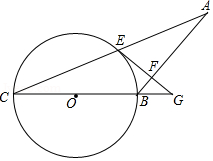
A、120° B、110° C、100° D、70°3. 下列计算正确的是( )A、2x+3y=5xy B、(﹣2x2)3=﹣6x6 C、3y2•(﹣y)=﹣3y2 D、6y2÷2y=3y4. 如图,是某几何体的三视图,则这个几何体是( ) A、圆锥 B、圆柱 C、球 D、三棱柱5. 在体育课上,甲、乙两名同学分别进行了5次跳远测试,经计算他们的平均成绩相同.若要比较这两名同学的成绩哪一个更为稳定,通常需要比较他们成绩的( )A、众数 B、平均数 C、中位数 D、方差6. 已知关于x的一元二次方程 有两个相等的实根,则k的值为( )A、 B、 C、2或3 D、 或7. 某工厂新引进一批电子产品,甲工人比乙工人每小时多搬运30件电子产品,已知甲工人搬运300件电子产品所用的时间与乙工人搬运200件电子产品所用的时间相同 若设乙工人每小时搬运x件电子产品,可列方程为A、 B、 C、 D、8. 如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=4,则半径OB等于( )
A、圆锥 B、圆柱 C、球 D、三棱柱5. 在体育课上,甲、乙两名同学分别进行了5次跳远测试,经计算他们的平均成绩相同.若要比较这两名同学的成绩哪一个更为稳定,通常需要比较他们成绩的( )A、众数 B、平均数 C、中位数 D、方差6. 已知关于x的一元二次方程 有两个相等的实根,则k的值为( )A、 B、 C、2或3 D、 或7. 某工厂新引进一批电子产品,甲工人比乙工人每小时多搬运30件电子产品,已知甲工人搬运300件电子产品所用的时间与乙工人搬运200件电子产品所用的时间相同 若设乙工人每小时搬运x件电子产品,可列方程为A、 B、 C、 D、8. 如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=4,则半径OB等于( ) A、 B、2 C、2 D、39. 如图,在矩形 中, ,点 分别在 上,则 的最小值是( )
A、 B、2 C、2 D、39. 如图,在矩形 中, ,点 分别在 上,则 的最小值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 分解因式: .11. 在一个不透明的袋子中装有除颜色外完全相同的5个红球、3个白球、2个绿球,任意摸出一球,摸到白球的概率是 .
12. 已知直线 y=ax(a≠0)与反比例函数 y= (k≠0)的图象一个交点 坐标为(2,4),则它们另一个交点的坐标是 .13. 原价100元的某商品,连续两次降价后售价为81元,若每次降低的百分率相同,则降低的百分率为 .
14. 如图,在边长为4的正方形ABCD中,以点B为圆心,以AB为半径画弧,交对角线BD于点E,则图中阴影部分的面积是(结果保留π)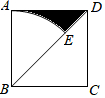 15. 如图,在Rt△ABC中,∠ACB = 90°,BC = 3,AC = 4,点D为边AB上一点.将△BCD沿直线CD翻折,点B落在点E处,联结AE.如果AE // CD,那么BE = .
15. 如图,在Rt△ABC中,∠ACB = 90°,BC = 3,AC = 4,点D为边AB上一点.将△BCD沿直线CD翻折,点B落在点E处,联结AE.如果AE // CD,那么BE = .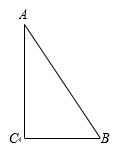
三、解答题
-
16. 计算: .17. 先化简,再求值: ,其中 .18. 如图,已知 , 在一条直线上, .

求证:
(1)、 ;(2)、四边形 是平行四边形.19. 我省中小学积极开展综合实践活动,某校准备组织开展四项综合实践活动:“A.我是非遗小传人,B.学做家常餐,C.爱心义卖行动,D.找个岗位去体验”.为了解学生最喜爱哪项综合实践活动,随机抽取部分学生进行问卷调查(每位学生只能选择一项),将调查结果绘制成下面两幅不完整的统计图,请结合图中提供的信息回答下列问题: (1)、本次一共调查了名学生,在扇形统计图中,m的值是;(2)、补全条形统计图;(3)、若该校共有1200名学生,估计最喜爱B和C项目的学生一共有多少名?(4)、现有最喜爱A,B,C,D活动项目的学生各一人,学校要从这四人中随机选取两人交流活动体会,请用列表或画树状图的方法求出恰好选取最喜爱C和D项目的两位学生的概率.20. 如图,某高速公路设计中需要测量某条江的宽度 ,测量人员使用无人机测量,在 处测得 两点的俯角分别为 和 ,若无人机离地面的高度 为 米,且点 在同一条水平直线上,求这条江的宽度 长(结果保留根号).
(1)、本次一共调查了名学生,在扇形统计图中,m的值是;(2)、补全条形统计图;(3)、若该校共有1200名学生,估计最喜爱B和C项目的学生一共有多少名?(4)、现有最喜爱A,B,C,D活动项目的学生各一人,学校要从这四人中随机选取两人交流活动体会,请用列表或画树状图的方法求出恰好选取最喜爱C和D项目的两位学生的概率.20. 如图,某高速公路设计中需要测量某条江的宽度 ,测量人员使用无人机测量,在 处测得 两点的俯角分别为 和 ,若无人机离地面的高度 为 米,且点 在同一条水平直线上,求这条江的宽度 长(结果保留根号).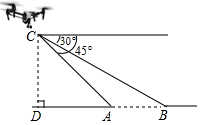 21. “低碳生活,绿色出行”的理念已深入人心,现在越来越多的人选择骑自行车上下班或外出旅游.周末,小红相约到郊外游玩,她从家出发0.5小时后到达甲地,玩一段时间后按原速前往乙地,刚到达乙地,接到妈妈电话,快速返回家中.小红从家出发到返回家中,行进路程y(km)随时间x(h)变化的函数图象大致如图所示.
21. “低碳生活,绿色出行”的理念已深入人心,现在越来越多的人选择骑自行车上下班或外出旅游.周末,小红相约到郊外游玩,她从家出发0.5小时后到达甲地,玩一段时间后按原速前往乙地,刚到达乙地,接到妈妈电话,快速返回家中.小红从家出发到返回家中,行进路程y(km)随时间x(h)变化的函数图象大致如图所示. (1)、小红从甲地到乙地骑车的速度为km/h;(2)、当1.5≤x≤2.5时,求出路程y(km)关于时间x(h)的函数解析式;并求乙地离小红家多少千米?
(1)、小红从甲地到乙地骑车的速度为km/h;(2)、当1.5≤x≤2.5时,求出路程y(km)关于时间x(h)的函数解析式;并求乙地离小红家多少千米?