青海省2019年数学中考仿真备考试卷

试卷更新日期：2020-01-15 类型：中考模拟

进入出卷网下载

一、单选题

1. 估计 $\sqrt{7} + 1$ 的值在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析

2. 下表是某公司员工月收入的资料：

月收入/元	45000	18000	10000	5500	5000	3400	3300	1000
人数	1	1	1	3	6	1	11	1

能够反映该公司全体员工月收入水平的统计量是（）

A、平均数和众数 B、平均数和中位数 C、中位数和众数 D、平均数和方差

查看试题解析

3. 某车间有27名工人，生产某种由一个螺栓套两个螺母的产品，每人每天生产螺母22个或螺栓16个.若分配x名工人生产螺栓，其他工人生产螺母，恰好使每天生产的螺栓和螺母配套.则下面所列方程中正确的是（）

A、2×16x=22（27﹣x） B、16x=22（27﹣x） C、22x=16（27﹣x） D、2×22x=16（27﹣x）

查看试题解析
4. 如图，⊙O的半径OD⊥弦AB于点C，连接BO并延长交⊙O于点E，连接AE，若AB=6，CD=1，则AE的长为（）

A、3 $\sqrt{3}$ B、8 C、12 D、8 $\sqrt{3}$

查看试题解析
5. 如图，在平行四边形ABCD中，E为AB边的中点，则S_△_BFC：S_△_CDF的值为（）

A、1：2 B、1：3 C、1：4 D、1：9

查看试题解析
6. 如图，将边长为 $\sqrt{3}$ 的正方形绕点B逆时针旋转30°，那么图中阴影部分的面积为（）

A、3 B、 $\sqrt{3}$ C、3﹣ $\sqrt{3}$ D、3﹣ $\frac{\sqrt{3}}{2}$

查看试题解析
7. 如图，在同一平面直角坐标系中，一次函数y₁=kx+b（k、b是常数，且k≠0）与反比例函数y₂= $\frac{c}{x}$ （c是常数，且c≠0）的图象相交于A（﹣3，﹣2），B（2，3）两点，则不等式y₁＞y₂的解集是（）

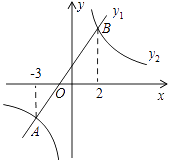A、﹣3＜x＜2 B、x＜﹣3或x＞2 C、﹣3＜x＜0或x＞2 D、0＜x＜2

查看试题解析
8. 如图，在△ABC中，∠B＝90°，AB＝3cm，BC＝6cm，动点P从点A开始沿AB向点B以1cm/s的速度移动，动点Q从点B开始沿BC向点C以2cm/s的速度移动，若P，Q两点分别从A，B两点同时出发，P点到达B点运动停止，则△PBQ的面积S随出发时间t的函数关系图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. ﹣5的倒数是， 9的平方根是， | $- \sqrt{3}$ |=.

查看试题解析
10. 计算： $\frac{x - y}{y} \cdot \frac{y}{x (x - y)}$ ＝．

查看试题解析
11. 将数12000000科学记数法表示为．

查看试题解析
12. 一个多边形的内角和是1800°，这个多边形是边形．

查看试题解析
13. 如图，△ABC中，∠C＝90°，∠ABC＝60°，BD平分∠ABC，则∠CDB＝度.

查看试题解析
14. 如图，a∥b，∠1＝110°，∠3＝40°，则∠2＝°.

查看试题解析
15. 计算：2a+3a＝．

查看试题解析
16. 从﹣2，﹣1，1，2四个数中，随机抽取两个数相乘，积为大于﹣4小于2的概率是．

查看试题解析
17. 一个扇形的圆心角为135°，弧长为3πcm，则此扇形的面积是cm².

查看试题解析
18. 经过已知点M和N的圆的圆心的轨迹是.

查看试题解析
19. 如图，小明想测量学校教学楼的高度，教学楼AB的后面有一建筑物CD，他测得当光线与地面成22°的夹角时，教学楼在建筑物的墙上留下高2米高的影子CE；而当光线与地面成45°的夹角时，教学楼顶A在地面上的影子F与墙角C有13米的距离（点B，F，C在同一条直线上），则AE之间的长为米.（结果精确到lm，参考数据：sin22°≈0.375，cos22°≈0.9375，tan22°≈0.4）

查看试题解析
20. 根据（x-1）（x+1）=x²-1，（x-1）（x²+x+1）=x³-1，（x-1）（x³+x²+x+1）=x⁴-1，…的规律，则可以得出2²⁰¹⁷+2²⁰¹⁶+2²⁰¹⁵+…+2³+2²+2+1的结果可以表示为。

查看试题解析

三、解答题

21. 计算： ${(\frac{1}{2})}^{- 2} - \sqrt{9} + (\sqrt{3} - 4)^{0} - \sqrt{2} \cos 45^{°}$ ．

查看试题解析
22. 计算：
解方程: $\frac{2 x + 9}{3 x - 9} = \frac{4 x - 7}{x - 3} + 2$ .

查看试题解析
23. 如图，AC是平行四边形ABCD的对角线.

(1)、利用尺规作出AC的垂直平分线（要求保留作图痕迹，不写作法）；

(2)、设AC的垂直平分线分别与AB，AC，CD交于点E，O，F，求证：以A、E、C、F为顶点的四边形为菱形.

查看试题解析
24. 某公司计划购进甲、乙两种规格的电脑，若购买甲种电脑3台，乙种电脑2台，共需资金23000元；若购买甲种电脑4台，乙种电脑3台，共需资金32000元.

(1)、甲、乙两种电脑每台的价格分别是多少元；

(2)、若公司计划购进这两种规格的电脑共20台，其中甲种电脑的数量不少于乙种电脑的数量，公司至多能够提供购买电脑的资金92000元，请设计几种购买方案供这个公司选择.

查看试题解析
25. 如图，AB为⊙O的直径，C、F为⊙O上两点，且点C为弧BF的中点，过点C作AF的垂线，交AF的延长线于点E，交AB的延长线于点D.

(1)、求证：DE是⊙O的切线；

(2)、如果半径的长为3，tanD= $\frac{3}{4}$ ，求AE的长.

查看试题解析

26. 某批足球的质量检测结果如下：

抽取足球数n	100	200	400	600	800	1000
合格的频数m	93	192	384	564	759	950
合格的频率 $\frac{m}{n}$	0.93	0.96	0.96	0.94

(1)、填写表中的空格；（结果保留0.01）

(2)、画出合格的频率的折线统计图；

(3)、从这批足球任意抽取的一只足球是合格品的概率是多少？并说明理由.

查看试题解析

27. 小儒在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考：

(1)、他认为该定理有逆定理，即“如果一个三角形某条边上的中线等于该边长的一半，那么这个三角形是直角三角形”应该成立，你能帮小儒证明一下吗？如图①，在△ABC中，AD是BC边上的中线，若AD＝BD＝CD，求证：∠BAC＝90°.

(2)、接下来，小儒又遇到一个问题：如图②，已知矩形ABCD，如果在矩形外存在一点E，使得AE⊥CE，求证：BE⊥DE，请你作出证明，可以直接用到第（1）问的结论.

(3)、在第（2）问的条件下，如果△AED恰好是等边三角形，直接用等式表示出此时矩形的两条邻边AB与BC的数量关系.

查看试题解析
28. 在平面直角坐标系xOy中，抛物线y＝ax²﹣（a+1）x﹣3与x轴交于A、B两点，点A的坐标为（﹣1，0）.

(1)、求B点与顶点D的坐标；

(2)、经过点B的直线l与y轴正半轴交于点M，S_△_ADM＝5，求直线l的解析式；

(3)、点P（t，0）为x轴上一动点，过点P作x轴的垂线m，将抛物线在直线m左侧的部分沿直线m对折，图象的其余部分保持不变，得到一个新图象G.请结合图象回答：当图象G与直线l没有公共点时，t的取值范围是.

查看试题解析