江苏省镇江市润州区2019年数学中考二模试卷

试卷更新日期：2020-01-15 类型：中考模拟

进入出卷网下载

一、单选题

1. 世界文化遗产长城总长约为6 700 000m，若将6 700 000用科学记数法表示为6.7×10ⁿ（n是正整数），则n的值为 ( )

A、5 B、6 C、7 D、8

查看试题解析
2. 如图是某一几何体的三视图，则这个几何体是（）

A、圆柱体 B、圆锥体 C、正方体 D、球体

查看试题解析
3. 某班六名同学体能测试成绩（分）如下：80，90，75，75，80，80，对这组数据表述错误的是（）

A、众数是80 B、极差是15 C、平均数是80 D、中位数是75

查看试题解析
4. 二次函数y＝ax²+bx+c图象上部分点的坐标满足下表：

x

…

-3

-2

-1

0

1

…

y

…

-3

-2

-3

-6

-11

…

则该函数图象上的点（﹣6，y₁），（m²+2m+3，y₂）则下列选项正确的是（）

A、y₁＞y₂ B、y₁≥y₂ C、y₁＜y₂ D、y₁≤y₂

查看试题解析
5. 如图，在平面直角坐标系中，对角线为1的正方形OABC，点A在x轴的正半轴上，如果以对角线OB为边作第二个正方形OBB₁C₁ ，再以对角线OB₁为边作第三个正方形OB_lB₂C₂ ，照此规律作下去，则点B₂₀₁₉的坐标为（）

A、（﹣2¹⁰⁰⁹ ， 2¹⁰⁰⁹） B、（2¹⁰⁰⁸ ， ﹣2¹⁰⁰⁸） C、（﹣2¹⁰⁰⁹ $\sqrt{2}$ ，0） D、（0，2¹⁰⁰⁸ $\sqrt{2}$ ）

查看试题解析

二、填空题

6. －5的相反数是．

查看试题解析
7. 计算（ $\sqrt{3} + 1$ ）（ $\sqrt{3} - 1$ ）的结果等于．

查看试题解析
8. 计算：a⁴÷a²=.

查看试题解析
9. 分解因式：x²﹣4x= ．

查看试题解析
10. 要使 $\sqrt{x - 3}$ 有意义，则x的取值范围是.

查看试题解析
11. 夏津农科所对甲、乙两种棉花试验田各5块进行试验后，得到甲、乙两个品种每母的平均产量相同，而甲、乙两个品种产量的方差分别为 $S_{甲}^{2} \approx 0.01$ ， $S_{乙}^{2} \approx 0.002$ ，则产量较为稳定的品种是（填“甲”或“乙”）。

查看试题解析
12. 已知圆锥的母线长是它底面圆半径的2倍，则它的侧面展开图的圆心角等于.

查看试题解析
13. 反比例函数y＝ $\frac{k + 1}{x}$ 的图象经过点(﹣1，2)，则k＝.

查看试题解析
14. 如图，A、B、C是⊙O的圆周上三点，∠ACB=40°，则∠ABO等于度.

查看试题解析
15. 如图，四边形ABCD中，∠BMF+∠CNF＝90°，E、F分别是AD、BC的中点，AB＝5，CD＝12，则EF＝.

查看试题解析
16. 已知，函数y＝ax²﹣6ax+9a+1与线段AB有交点，且已知点A（0，1）与点B（2，3）的坐标，则a的取值范围.

查看试题解析
17. 在直角坐标系中，点E（10，0），F（0，5），A（﹣1，0），D（0，2），四边形ABCD为菱形，且点B、C在第二象限，向右平移菱形ABCD，平移的距离为d，当点B在△EOF边及内部时，d的范围是.

查看试题解析

三、解答题

18.

(1)、 ${(- 1)}^{3} + {(\sqrt{5} + 1)}^{0} + \cos 30^{0}$

(2)、 $(a^{2} - 1) \div (1 - \frac{1}{a})$

查看试题解析
19.

(1)、解方程： $\frac{1}{2 x - 4} + \frac{1}{2} = \frac{3}{2 - x}$

(2)、解不等式组： ${\begin{array}{l} 1 - 2 x > 0 \\ 2 x + 6 \geq 0 \end{array}$

查看试题解析

20. 上海世博园开放后，前往参观的人非常多.5月中旬的一天某一时段，随机调查了部分入园游客，统计了他们进园前等候检票的时间，并绘制成如下图表.表中“10~20”表示等候检票的时间大于或等于10min而小于20min，其它类同.

时间分段/min	频数/人数	频率
10~20	8	0.200
20~30	14	a
30~40	10	0.250
40~50	b	0.125
50~60	3	0.075
合计	c	1.000

(1)、这里采用的调查方式是；

(2)、求表中a、b、c的值，并请补全频数分布直方图；

(3)、在调查人数里，等候时间少于40min的有人；

(4)、此次调查中，中位数所在的时间段是~min.

查看试题解析

21. 如图，有A，B两个转盘，其中转盘A被分成4等份，转盘B被分成3等份，并在每一份内标上数字．现甲、乙两人同时各转动其中一个转盘，转盘停止后（当指针指在边界线上时视为无效，重转），若将A转盘指针指向的数字记为x，B转盘指针指向的数字记为y，从而确定点P的坐标为P（x，y）．

(1)、请用列表或画树状图的方法写出所有可能得到的点P的坐标；

(2)、计算点P在函数y= $\frac{6}{x}$ 图象上的概率．

查看试题解析
22. 如图，在平行四边形ABCD中，

(1)、以BD为对角线，作菱形MBND，使得M、N分别在BA、DC的延长线上.（保留作图痕迹，不写作图过程）

(2)、证明所作四边形MBND是菱形.

查看试题解析
23.
已知B港口位于A观测点北偏东53.2°方向，且其到A观测点正北方向的距离BD的长为16km，一艘货轮从B港口以40km/h的速度沿如图所示的BC方向航行，15min后达到C处，现测得C处位于A观测点北偏东79.8°方向，求此时货轮与A观测点之间的距离AC的长（精确到0.1km）．（参考数据：sin53.2°≈0.80，cos53.2°≈0.60，sin79.8°≈0.98，cos79.8°≈0.18，tan26.6°≈0.50， $\sqrt{2}$ ≈1.41， $\sqrt{5}$ ≈2.24）

查看试题解析
24. 某超市购进一批牛肉销售，经过还价，实际价格每千克比原来少2元，发现原来买这批牛肉32千克的钱，现在可买33千克.

(1)、现在实际购进这批牛肉每千克多少元？

(2)、若这批牛肉的销售量y（千克）与销售单价x（元/千克）满足如图所示的一次函数关系.求y与x之间的函数关系式；

(3)、这批牛肉的销售单价定为多少时，能获得最大利润？最大利润是多少？（利润＝销售收入﹣进货金额）

查看试题解析
25. 某公司为了扩大经营，决定购进6台机器用于生产某活塞.现有甲、乙两种机器供选择，其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算，本次购买机器所耗资金不能超过34万元.

甲

乙

价格(万元/台)

7

5

每台日产量(个)

100

60

(1)、按该公司要求可以有几种购买方案？

(2)、如果该公司购进的6台机器的日生产能力不能低于380个，那么为了节约资金应选择什么样的购买方案？

查看试题解析
26. 如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB于点F，连接BE.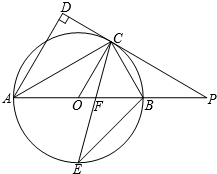

(1)、求证：AC平分∠DAB；

(2)、求证：△PCF是等腰三角形；

(3)、若tan∠ABC= $\frac{4}{3} ， B E = 7 \sqrt{2}$ ，求线段PC的长.

查看试题解析
27. 如图，已知二次函数y＝ax²+bx+c（a≠0）的图象与直线AB相交，与x轴、y轴交于A（2，0）、B（0，2 $\sqrt{3}$ ）.

(1)、求点O关于AB的对称点P的坐标；

(2)、若点P在二次函数y＝ax²+bx+c（a≠0）的图象上，求二次函数y＝ax²+bx+c（a≠0）的关系式.

(3)、在（2）的条件下，在△ABP内存在点M，使得MA+MB+MP的值最小，则相应点M的坐标为.

查看试题解析
28. 如图，在菱形ABCD中，边长为2 $\sqrt{3}$ ，∠BAD＝120°，点P从点B开始，沿着B→D方向，速度为每秒1个单位，运动到点D停止，设运动的时间为t（秒），将线段AP绕点A逆时针旋转60°，得到对应线段的延长线与过点P且垂直AP的垂线段相交于点E，

（ $\sqrt{3}$ ≈1.73，sin11°≈0.19，cos11°≈0.98，sin19°≈0.33，tan19°≈0.34，sin41°≈0.65，tan41°≈0.87）

(1)、当t＝0时，求AE的值.

(2)、P点在运动过程中，线段PE与菱形的边框交于点F.（精确到0.1）
问题1：如图2，当∠BAP＝11°，AF＝2PF，则OQ＝.

问题2：当t为何值时，△APF是含有30°角的直角三角形，写出所有符合条件的t的值.

(3)、当点P在运动过程中，求出△ACE的面积y关于时间t的函数表达式.（请说明理由）

查看试题解析

x	…	-3	-2	-1	0	1	…
y	…	-3	-2	-3	-6	-11	…

	甲	乙
价格(万元/台)	7	5
每台日产量(个)	100	60