江苏省扬州市2019年数学中考三模试卷

试卷更新日期：2020-01-15 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列说法正确的是（）

A、0是无理数 B、π是有理数 C、4是有理数 D、 $\frac{\sqrt{2}}{2}$ 是分数

查看试题解析
2. 12月2日，2018年第十三届南宁国际马拉松比赛开跑，2.6万名跑者继续刷新南宁马拉松的参与人数纪录!把2.6万用科学记数法表示为（）

A、 0.26×10³ B、2.6×10³ C、0.26×10⁴ D、2.6×10⁴

查看试题解析
3. 下列计算错误的是（）

A、4x³•2x²=8x⁵ B、a⁴﹣a³=a C、（﹣x²）⁵=﹣x¹⁰ D、（a﹣b）²=a²﹣2ab+b²

查看试题解析
4. 已知一个几何体及其左视图如图所示，则该几何体的主视图是（）

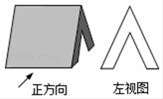A、 B、 C、 D、

查看试题解析
5. 如图，下列条件中，不能判断直线 $a / / b$ 的是 $($ $)$

A、 $∠ 1 + ∠ 3 = 180^{\circ}$ B、 $∠ 2 = ∠ 3$ C、 $∠ 4 = ∠ 5$ D、 $∠ 4 = ∠ 6$

查看试题解析
6. 解分式方程 $\frac{1 - x}{x - 2} = \frac{1}{2 - x} - 2$ 时，去分母变形正确的是（）

A、 $- 1 + x = - 1 - 2 (x - 2)$ B、 $1 - x = 1 - 2 (x - 2)$ C、 $- 1 + x = 1 + 2 (2 - x)$ D、 $1 - x = - 1 - 2 (x - 2)$

查看试题解析
7. 数学课上，小明进行了如下的尺规作图（如图所示）：
（ 1 ）在△AOB（OA＜OB）边OA、OB上分别截取OD、OE，使得OD=OE；（2）分别以点D、E为圆心，以大于 $\frac{1}{2}$ DE为半径作弧，两弧交于△AOB内的一点C；（3）作射线OC交AB边于点P.那么小明所求作的线段OP是△AOB的（）

A、一条中线 B、一条高 C、一条角平分线 D、不确定

查看试题解析
8. 如图，平面内一个⊙O半径为4，圆上有两个动点A，B，以AB为边在圆内作一个正方形ABDC，则OD的最小值是（）

A、2 B、 $\frac{4 \sqrt{5}}{5}$ C、2 $\sqrt{3}$ ﹣2 D、4 $\sqrt{2}$ ﹣4

查看试题解析

二、填空题

9. 若a，b都是实数，b＝ $\sqrt{1 - 2 a}$ + $\sqrt{2 a - 1}$ ﹣2，则a^b的值为.

查看试题解析
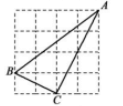
10. 如图。在 $4 \times 4$ 的正方形方格图形中，小正方形的顶点称为格点. $Δ A B C$ 的顶点都在格点上，则 $∠ B A C$ 的正弦值是.

查看试题解析
11. 因式分解：9a³b﹣ab＝.

查看试题解析
12. 已知关于x的方程（k﹣1）x²﹣2kx+k﹣3=0有两个相等的实根，则k的值是．

查看试题解析
13. 如图，李明从A点出发沿直线前进5米到达B点后向左旋转的角度为α，再沿直线前进5米，到达点C后，又向左旋转α角度，照这样走下去，第一次回到出发地点时，他共走了45米，则每次旋转的角度α为.

查看试题解析
14. 如图，一次函数y＝ax+b的图象经过A（2，0）、B（0，﹣1）两点，则关于x的不等式ax+b＜0的解集是.

查看试题解析
15. 已知圆锥的底面半径是2，母线长是4，则圆锥的侧面积是．

查看试题解析
16. 反比例函数 $y = - \frac{1}{x}$ 图像上三点的坐标分别为A（-1，y₁）,B(1，y₂），C（3，y₃）,则y₁ ， y_2, ， y₃的大小关系是。（用“＞”连接）

查看试题解析
17. 如图，边长为2的正方形ABCD中心与半径为2的⊙O的圆心重合，E、F分别是AD、BA的延长与⊙O的交点，则图中阴影部分的面积是.(结果保留 $π$ )

查看试题解析
18. 如图1，则等边三角形ABC中，点P为BC边上的任意一点，且∠APD＝60°，PD交AC于点D，设线段PB的长度为x，CD的长度为y，若y与x的函数关系的大致图象如图2，则等边三角形ABC的面积为.

查看试题解析

三、解答题

19.

(1)、计算：2cos60°﹣ $(\sqrt{2019} - π) 0 + \sqrt[3]{- 8} - {(\frac{1}{3})}^{- 2}$

(2)、解不等式组： ${\begin{array}{l} 2 x + 4 \leq 3 (x + 2) \\ \frac{x - 1}{2} - \frac{x - 1}{4} < 1 \end{array}$ ，并求不等式组的整数解.

查看试题解析
20. 先化简，再求值：（ $\frac{1}{x - 1}$ +1）÷ $\frac{x}{x^{2} - 1}$ ，其中x是方程x²+3x=0的根．

查看试题解析
21. 七年级教师对试卷讲评课中学生参与的深度与广度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项：评价组随机抽取了若干名初中学生的参与情况，绘制成如图所示的频数分布直方图和扇形统计图（均不完整），请根据图中所给信息解答下列问题：

(1)、在这次评价中，一共抽查了名学生；

(2)、在扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数为度；

(3)、请将频数分布直方图补充完整；

(4)、如果全市有8600名七年级学生，那么在试卷评讲课中，“独立思考”的七年级学生约有多少人？

查看试题解析
22. 现如今，“垃圾分类”意识已深入人心，如图是生活中的四个不同的垃圾分类投放桶.其中甲投放了一袋垃圾，乙投放了两袋垃圾.

(1)、直接写出甲投放的垃圾恰好是“厨余垃圾”的概率；

(2)、求乙投放的两袋垃圾不同类的概率.

查看试题解析
23. 某市五月遭遇了持续强降雨，造成部分地区洪涝灾害，某爱心组织紧急筹集了部分资金，计划购买甲、乙两种救灾物品共4000件送往灾区，已知每件甲种物品的价格比每件乙种物品的价格贵10元，用300元购买甲种物品的件数恰好与用240元购买乙种物品的件数相同.

(1)、求甲、乙两种救灾物品每件的价格各是多少元？

(2)、经调查，灾区对乙种物品件数的需求量是甲种物品件数的3倍，若该爱心组织按照此需求的比例购买这4000件物品，需筹集资金多少元？

查看试题解析
24. 如图，四边形ABCD为矩形，点E是边BC的中点，AF∥ED，AE∥DF

(1)、求证：四边形AEDF为菱形；

(2)、试探究：当AB：BC＝，菱形AEDF为正方形？请说明理由.

查看试题解析
25. 已知：如图，△ABC内接于⊙O，AD为⊙O的弦，∠1＝∠2，DE⊥AB于E，DF⊥AC于F.求证：BE＝CF.

查看试题解析
26. 如图，是一座古拱桥的截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为10m时，桥洞与水面的最大距离是5m.

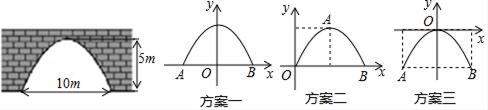(1)、经过讨论，同学们得出三种建立平面直角坐标系的方案（如图），你选择的方案是（填方案一，方案二，或方案三），则B点坐标是，求出你所选方案中的抛物线的表达式；

(2)、因为上游水库泄洪，水面宽度变为6m，求水面上涨的高度.

查看试题解析
27. 已知在梯形ABCD中，AD∥BC ， AC＝BC＝10，cos∠ACB＝ $\frac{4}{5}$ ，点E在对角线AC上（不与点A、C重合），∠EDC＝∠ACB ， DE的延长线与射线CB交于点F ，设AD的长为x ．

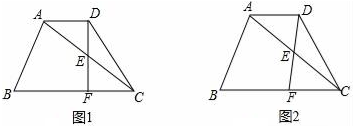(1)、如图1，当DF⊥BC时，求AD的长；

(2)、设EC＝y ，求y关于x的函数解析式，并直接写出定义域；

(3)、当△DFC是等腰三角形时，求AD的长．

查看试题解析
28. 如图，抛物线y＝ax²+bx（a＞0）过点E（8，0），矩形ABCD的边AB在线段OE上（点A在点B的左侧），点C、D在抛物线上，∠BAD的平分线AM交BC于点M，点N是CD的中点，已知OA＝2，且OA：AD＝1：3.

(1)、求抛物线的解析式；

(2)、F、G分别为x轴，y轴上的动点，顺次连接M、N、G、F构成四边形MNGF，求四边形MNGF周长的最小值；

(3)、在x轴下方且在抛物线上是否存在点P，使△ODP中OD边上的高为 $\frac{6 \sqrt{10}}{5}$ ？若存在，求出点P的坐标；若不存在，请说明理由；

(4)、矩形ABCD不动，将抛物线向右平移，当平移后的抛物线与矩形的边有两个交点K、L，且直线KL平分矩形的面积时，求抛物线平移的距离.

查看试题解析