贵州省遵义市汇川区2019届九年级第一次中考适应性考试数学试卷

试卷更新日期：2020-01-15 类型：中考模拟

进入出卷网下载

一、单选题

1. 当x=﹣1时，代数式3x+1的值是（）

A、﹣1 B、﹣2 C、4 D、﹣4

查看试题解析
2. 在下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 为贯彻落实觉中央、国务院关于推进城乡义务教育一体化发展的部署，教育部会同有关部门近五年来共新建、改扩建校舍186000000平方米，其中数据186000000用科学记数法表示是（）

A、1.86×107 B、186×106 C、1.86×108 D、0.186×109

查看试题解析
4. 下列计算正确的是（）

A、a⁴+a⁵=a⁹ B、（2a²b³）²=4a⁴b⁶ C、﹣2a（a+3）=﹣2a²+6a D、（2a﹣b）²=4a²﹣b²

查看试题解析
5. 如图所示，直线a∥b，∠1=35°，∠2=90°，则∠3的度数为（）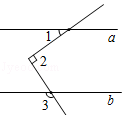

A、125° B、135° C、145° D、155°

查看试题解析
6. 在一次数学答题比赛中，五位同学答对题目的个数分别为7，5，3，5，10，则关于这组数据的说法不正确的是（）

A、众数是5 B、中位数是5 C、平均数是6 D、方差是3.6

查看试题解析
7. 由若干个完全相同的小正方体组成一个立体图形，它的左视图和俯视图如图所示，则小正方体的个数不可能是（）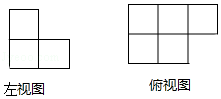

A、5 B、6 C、7 D、8

查看试题解析
8. 现有4张卡片，其中3张卡片正面上的图案是“ ”，1张卡片正面上的图案是“ ”，它们除此之外完全相同．把这4张卡片背面朝上洗匀，从中随机抽取两张，则这两张卡片正面图案相同的概率是（）

A、 $\frac{9}{16}$ B、 $\frac{3}{4}$ C、 $\frac{3}{8}$ D、 $\frac{1}{2}$

查看试题解析
9. 如图，AB是⊙O的直径，点D为⊙O上一点，且∠ABD=30°，BO=4，则 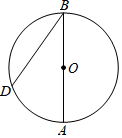$\overset{⌢}{B D}$ 的长为（）

A、 $\frac{2}{3} π$ B、 $\frac{4}{3} π$ C、2π D、 $\frac{8}{3} π$

查看试题解析
10. 如图，在平面直角坐标系中，点A，C在x轴上，点C的坐标为（﹣1，0），AC=2．将Rt△ABC先绕点C顺时针旋转90°，再向右平移3个单位长度，则变换后点A的对应点坐标是（）

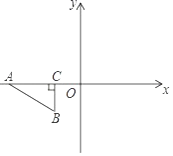A、（2，2） B、（1，2） C、（﹣1，2） D、（2，﹣1）

查看试题解析
11. 如图所示，在正方形ABCD中，G为CD边中点，连接AG并延长交BC边的延长线于E点，对角线BD交AG于F点．已知FG=2，则线段AE的长度为（）

A、6 B、8 C、10 D、12

查看试题解析
12. 抛物线y=ax²+bx+c的对称轴为直线x=﹣1，部分图象如图所示，下列判断中：
①abc＞0；②b²﹣4ac＞0；③9a﹣3b+c=0；④若点（﹣0.5，y₁），（﹣2，y₂）均在抛物线上，则y₁＞y₂；⑤5a﹣2b+c＜0．其中正确的个数有（）

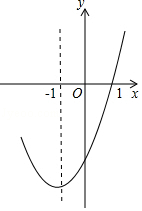A、2 B、3 C、4 D、5

查看试题解析

二、填空题

13. 函数y= $\frac{\sqrt{2 x + 1}}{x - 3}$ 的自变量x的取值范围是．

查看试题解析
14. 我们规定：等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”，记作k，若k= $\frac{1}{2}$ ，则该等腰三角形的顶角为度．

查看试题解析
15. 不等式组 ${\begin{matrix} x + 5 > 2 \\ 4 - x \geq 3 \end{matrix}$ 的最小整数解是．

查看试题解析
16. 如图，过x轴上任意一点P作y轴的平行线，分别与反比例函数y= $\frac{3}{x}$ （x＞0），y=﹣ $\frac{6}{x}$ （x＞0）的图象交于A点和B点，若C为y轴任意一点.连接AB、BC，则△ABC的面积为.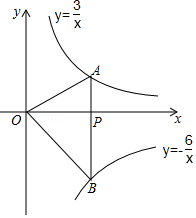

查看试题解析

三、解答题

17. 计算：

(1)、 $(a + 1) (a - 1) - {(a - 2)}^{2}$ ；

(2)、 $2 (\sqrt{8} - 1) + | - 3 | - {(\sqrt{3} - 1)}^{0}$

查看试题解析
18. 先化简，再求值： $\frac{1}{x^{2} + 2 x + 1} \cdot (1 + \frac{3}{x - 1}) \div \frac{x + 2}{x^{2} - 1}$ ，其中x=2 $\sqrt{5}$ ﹣1．

查看试题解析
19. 如图，方格纸中每个小正方形的边长均为1，线段AB的两个端点均在小正方形的顶点上.

①在图中画出以线段AB为一边的矩形ABCD（不是正方形），且点C和点D均在小正方形的顶点上；

②在图中画出以线段AB为一腰，底边长为2 $\sqrt{2}$ 的等腰三角形ABE，点E在小正方形的顶点上，连接CE，请直接写出线段CE的长.

查看试题解析
20. 图1是一种折叠门，由上下轨道和两扇长宽相等的活页门组成，整个活页门的右轴固定在门框
上，通过推动左侧活页门开关；图2是其俯视图简化示意图，已知轨道 $A B = 120 c m$ ，两扇活页门的宽 $O C = O B = 60 c m$ ，点 $B$ 固定，当点 $C$ 在 $A B$ 上左右运动时， $O C$ 与 $O B$ 的长度不变(所有结果保留小数点后一位).

(1)、若 $∠ O B C = 50 °$ ，求 $A C$ 的长；

(2)、当点 $C$ 从点 $A$ 向右运动60 $c m$ 时，求点 $O$ 在此过程中运动的路径长.
（参考数据：sin50°≈0.77， cos50°≈0.64， tan50°≈1.19， π取3.14）

查看试题解析
21. 文化是一个国家、一个民族的灵魂，近年来，央视推出《中国诗词大会》、《中国成语大会》、《朗读者》、《经曲咏流传》等一系列文化栏目.为了解学生对这些栏目的喜爱情况，某学校组织学生会成员随机抽取了部分学生进行调查，被调查的学生必须从《经曲咏流传》（记为A）、《中国诗词大会》（记为B）、《中国成语大会》（记为C）、《朗读者》（记为D）中选择自己最喜爱的一个栏目，也可以写出一个自己喜爱的其他文化栏目（记为E）.根据调查结果绘制成如图所示的两幅不完整的统计图.

请根据图中信息解答下列问题：

(1)、在这项调查中，共调查了多少名学生？

(2)、将条形统计图补充完整，并求出扇形统计图中“B”所在扇形圆心角的度数；

(3)、若选择“E”的学生中有2名女生，其余为男生，现从选择“E”的学生中随机选出两名学生参加座谈，请用列表法或画树状图的方法求出刚好选到同性别学生的概率.

查看试题解析
22. 某乡镇实施产业扶贫，帮助贫困户承包了荒山种植某品种蜜柚.到了收获季节，已知该蜜柚的成本价为8元/千克，投入市场销售时，调查市场行情，发现该蜜柚销售不会亏本，且每天销售量 $y$ (千克)与销售单价 $x$ (元/千克)之间的函数关系如图所示.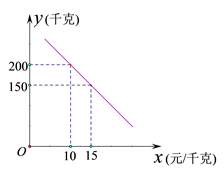

(1)、求 $y$ 与 $x$ 的函数关系式，并写出 $x$ 的取值范围；

(2)、当该品种蜜柚定价为多少时，每天销售获得的利润最大？最大利润是多少？

(3)、某农户今年共采摘蜜柚4800千克，该品种蜜柚的保质期为40天，根据(2)中获得最大利润的方式进行销售，能否销售完这批蜜柚？请说明理由.

查看试题解析
23. 已知，点 $M$ 为二次函数 $y = - {(x - b)}^{2} + 4 b + 1$ 图象的顶点，直线 $y = m x + 5$ 分别交 $x$ 轴正半轴， $y$ 轴于点 $A ， B$ .

(1)、如图1，若二次函数图象也经过点 $A ， B$ ，试求出该二次函数解析式，并求出 $m$ 的值.

(2)、如图2，点 $A$ 坐标为 $(5 ， 0)$ ，点 $M$ 在 $Δ A O B$ 内，若点 $C (\frac{1}{4} ， y_{1})$ ， $D (\frac{3}{4} ， y_{2})$ 都在二次函数图象上，试比较 $y_{1}$ 与 $y_{2}$ 的大小.

查看试题解析
24. 如图，已知 $P$ 为锐角 $∠ M A N$ 内部一点，过点 $P$ 作 $P B ⊥ A M$ 于点 $B$ ， $P C ⊥ A N$ 于点 $C$ ，以 $P B$ 为直径作 $⊙ O$ ，交直线 $C P$ 于点 $D$ ，连接 $A P ， B D$ ， $A P$ 交 $⊙ O$ 于点 $E$ .

(1)、求证： $∠ B P D = ∠ B A C$ .

(2)、连接 $E B ， E D$ ，当 $\tan ∠ M A N = 2$ ， $A B = 2 \sqrt{5}$ 时，在点 $P$ 的整个运动过程中.
①若 $∠ B D E = 45^{\circ}$ ，求 $P D$ 的长.

②若 $Δ B E D$ 为等腰三角形，求所有满足条件的 $B D$ 的长.

(3)、连接 $O C ， E C$ ， $O C$ 交 $A P$ 于点 $F$ ，当 $\tan ∠ M A N = 1$ ， $O C / / B E$ 时，记 $Δ O F P$ 的面积为 $S_{1}$ ， $Δ C F E$ 的面积为 $S_{2}$ ，请写出 $\frac{S_{1}}{S_{2}}$ 的值.

查看试题解析