贵州省遵义市2019年数学中考一模试卷

试卷更新日期：2020-01-15 类型：中考模拟

进入出卷网下载

一、单选题

1. 5的倒数是（）

A、 $\frac{1}{5}$ B、 $- 5$ C、 $- \frac{1}{5}$ D、 $5$

查看试题解析
2. 下面每个图形都是由6个边长相同的正方形拼成的图形，其中能折叠成正方体的是（）

A、 B、 C、 D、

查看试题解析
3. 商务部发布数据显示，2019年春节黄金同期间，全国商品市场保持平稳较快增长.除夕至正月初六，全国零售和餐饮企业实现销售额约10050亿元、把10050亿这个数字用科学记数法表示为（）

A、 $1.0050 \times 10^{4}$ B、 $1.0050 \times 10^{9}$ C、 $1.0050 \times 10^{12}$ D、 $1.0050 \times 10^{13}$

查看试题解析
4. 中央电视台举行中国诗词大会，在某一场的比赛中，五位选手答对的题目数分别是8，6，7，8，9，则关于这组数据的说法不正确的是（）

A、众数是8 B、中位数是8 C、极差是3 D、平均数是8

查看试题解析
5. 下面四个运算，计算正确的一个是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(- 3 a b c^{3})}^{2} = 9 a^{2} b^{2} c^{2}$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 $3 x y^{3} - 4 x^{2} y = x y (3 y^{2} - 4 x)$

查看试题解析
6. 将一幅三角板如图所示摆放，若BC∥DE，那么∠1的度数为（）

A、 $45^{\circ}$ B、 $60^{\circ}$ C、 $75^{\circ}$ D、 $80^{\circ}$

查看试题解析
7. 如图，在△ABC中，∠ABC=90°，AC=4，AB=2 $\sqrt{3}$ ，以C为圆心，BC之长为半径的弧交边AC于点D，则图中阴影部分的面积为（）

A、 $2 \sqrt{3} - \frac{2}{3} π$ B、 $\frac{2}{3} π$ C、 $2 \sqrt{3} - \frac{4}{3} π$ D、 $\frac{4}{3} π$

查看试题解析
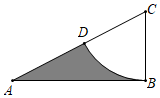8. 已知两个函数y₁=k₁x+b与y₂= $\frac{k_{2}}{x}$ 的图象如图所示，其中A（-1，2），B（2，-1），则不等式k₁x+b＞ $\frac{k_{2}}{x}$ 的解集为（）

A、 $x < - 1$ 或 $x > 2$ B、 $x < - 1$ 或 $0 < x < 2$ C、 $- 1 < x < 2$ D、 $- 1 < x < 0$ 或 $0 < x < 2$

查看试题解析
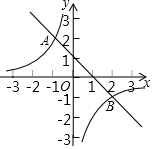9. 如图，点P是四边形ABCD内的一点，AP平分∠DAB，BP平分∠ABC，设∠C+∠D的大小为x，∠P的大小为y，则x，y的关系是（）

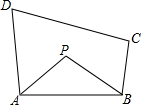A、 $y = 2 x - 180^{\circ}$ B、 $y = \frac{1}{2} x$ C、 $y = \frac{1}{3} x$ D、 $y = 180^{\circ} - \frac{1}{2} x$

查看试题解析
10. 如图，E，F是平行四边形ABCD对角线BD上的两点，DE=EF=BF，连接CE并延长交AD于点G，连接CF并延长交AB于点H，连接CH，设△CDG的面积为S₁ ， △CHG的面积为S₂ ，则S₁与S₂的关系正确的是（）

A、 $S_{1} = S_{2}$ B、 $S_{1} = \frac{1}{3} S_{2}$ C、 $S_{1} = \frac{2}{3} S_{2}$ D、 $S_{1} = \frac{1}{2} S_{2}$

查看试题解析

二、填空题

11. 已知x₁ ， x₂是关于x的方程x²-（2m-2）x+（m²-2m）=0的两根，且满足x₁•x₂+2（x₁+x₂）=-1，那么m的值为（）

A、 $- 1$ 或3 B、 $- 3$ 或1 C、 $- 3$ D、1

查看试题解析
12. 如图，抛物线y=ax²+bx+c与x轴交于点（-1，0），顶点坐标为（1，m），与y轴交点在（0，3），（0，4）之（不包含端点），现有下列结论：①3a+b＞0；②- $\frac{4}{3}$ ＜a＜-1；③关于x的方程ax²+bx+c=m-2有两个不相等的实数根：④若点M（-1.5，y₁），N（2.5，y₂）是函数图象上的两点，则y₁=y₂.其中正确结论的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
13. 若a+ $\frac{1}{a}$ = $\sqrt{5}$ ，则a²+ $\frac{1}{a^{2}}$ =.

查看试题解析
14. 小明有5根小棒，长度分别为3cm，4cm，5cm，6cm，7cm，现从中任选3根小棒，怡好能搭成三角形的概率是

查看试题解析
15. 在平面直角坐标系xOy中，点A（-2，m）绕坐标原点O顺时针旋转90°后，恰好落在图中⊙P中的阴影区域（包括边界）内，⊙P的半径为1，点P的坐标为（3，2），则m的取值范围是.

查看试题解析
16. 如图所示，是一个运算程序示意图，若第一次输人k的值为216，则第2019次输出的结果是.

查看试题解析

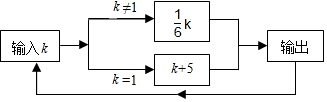
三、解答题

17. 先化简，再求值： $(\frac{x - 1}{x} - \frac{x - 2}{x + 1}) \div \frac{2 x^{2} - x}{x^{2} + 2 x + 1}$ ，其中x满足x²－2x－2=0.

查看试题解析
18. 北盘江大桥坐落于云南宜威与贵州水城交界处，横跨云贵两省，为目前世界第一高桥图1是大桥的实物图，图2是从图1中引申出的平面图，测得桥护栏BG=1.8米，拉索AB与护栏的夹角是26°，拉索ED与护栏的夹角是60°，两拉索底端距离BD为300m，若两拉索顶端的距离AE为90m，请求出立柱AH的长.（tan26°≈0.5，sin26°≈0.4， $\sqrt{3} \approx$ 1.7）

查看试题解析
19.

(1)、计算：-3²+2tan60°-|2 $\sqrt{3}$ -3|；

(2)、解不等式组： ${\begin{matrix} 3 x > x + 2 \\ x + 4 \leq 2 (2 x - 1) \end{matrix}$

查看试题解析
20. 如图，有边长为a的正方形卡片①，边长为b的正方形卡片②，两邻边长分别为a，b的矩形卡片③若干张.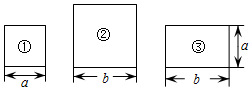

(1)、请用2张卡片①，1张卡片②，3张卡片③拼成一个矩形，在方框中画出这个矩形的草图；

(2)、请结合拼图前后面积之间的关系写出一个等式；

(3)、小明想用类似方法解释多项式乘法（a+3b）（2a+2b）的结果，那么需用卡片①张，卡片②张，卡片③张.

查看试题解析
21. 某校七年级10个班的300名学生即将参加学校举行的研究旅行活动，学校提出以下4个活动主题：A.赤水丹霞地貌考察；B.平塘天文知识考察；C.山关红色文化考察；D.海龙电土司文化考察，为了解学生喜欢的活动主题，学生会开展了一次调查研究，请将下面的过程补全

(1)、收集数据：学生会计划调查学生喜欢的活动主题情况，下面抽样调查的对象选择合理的是.（填序号）
①选择七年级3班、4班、5班学生作为调查对象

②选择学校旅游摄影社团的学生作为调查对象

③选择各班学号为6的倍数的学生作为调查对象

(2)、整理、描述数据：通过调査后，学生会同学绘制了如下两幅不完整的统计图，请把统计图补充完整
某校七年级学生喜欢的活动主题条形统计图某校七年级学生喜欢的活动主题扇形统计图

(3)、分析数据、推断结论：请你根据上述调查结果向学校推荐本次活动的主题，你的推荐是（填A-D的字母代号），估算全年级大约有多少名学生喜欢这个主题活动

(4)、若在5名学生会干部（3男2女）中，随机选取2名同学担任活动的组长和副组长，求抽出的两名同学恰好是1男1女的概率.

查看试题解析
22. 有大小两种货车，3辆大货车与4辆小货车一次可以运货18吨，2辆大货车与6辆小货车一次可以运货17吨.

(1)、请问1辆大货车和1辆小货车一次可以分别运货多少吨？

(2)、目前有33吨货物需要运输，货运公司拟安排大小货车共计10辆，全部货物一次运完，其中每辆大货车一次运费花费130元，每辆小货车一次运货花费100元，请问货运公司应如何安排车辆最节省费用？

查看试题解析
23. 如图，已知△ABC内接于⊙O，AB是直径，点D在⊙O上，OD∥BC，过点D作DE⊥AB，垂足为E，连接CD交OE边于点F.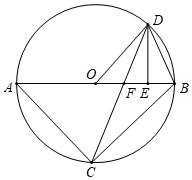

(1)、求证：△DOE∽△ABC；

(2)、求证：∠ODF=∠BDE；

(3)、连接OC.设△DOE的面积为S.sinA= $\frac{2}{3}$ ，求四边形BCOD的面积（用含有S的式子表示）

查看试题解析
24. 在平面直角坐标系中，二次函数y=-x²-bx+c的图象经过点A，点B（1，0）和点C（0，3）.点D是抛物线的顶点.

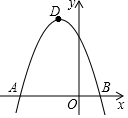(1)、求二次函数的解析式和点D的坐标

(2)、直线y=kx+n（k≠0）与抛物线交于点M，N，当△CMN的面积被y轴平分时，求k和n应满足的条件

(3)、抛物线的对称轴与x轴交于点E，将抛物线向下平移m（m＞0）个单位，平移后抛物线与y轴交于点C′，连接DC′，OD，是否存在OD平分∠C′DE的情况？若存在，求出m的值；若不荐在，请说明理由.

查看试题解析