贵州省毕节市2019年初中毕业生学业(升学)统一考试模拟试卷数学试卷
试卷更新日期:2020-01-15 类型:中考模拟
一、单选题
-
1. 3的相反数是( )A、﹣3 B、3 C、 D、﹣2. 下列几何体的左视图为长方形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2018年我市用于资助贫困学生的助学金总额是445800000元,将445800000用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( ).A、 B、 C、 D、5. 在平面内,将一个直角三角板按如图所示摆放在一组平行线上;若∠1=55°,则∠2的度数是( )
3. 2018年我市用于资助贫困学生的助学金总额是445800000元,将445800000用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是( ).A、 B、 C、 D、5. 在平面内,将一个直角三角板按如图所示摆放在一组平行线上;若∠1=55°,则∠2的度数是( ) A、50° B、45° C、40° D、35°6. 若一个正比例函数的图象经过A(3,-6),B(m,-4)两点,则m的值为( )A、2 B、8 C、-2 D、-87. 黄金分割数 是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算 ﹣1的值( )A、在1.1和1.2之间 B、在1.2和1.3之间 C、在1.3和1.4之间 D、在1.4和1.5之间8. 如图是成都市某周内日最高气温的折线统计图,关于这7天的日最高气温的说法正确的是( )
A、50° B、45° C、40° D、35°6. 若一个正比例函数的图象经过A(3,-6),B(m,-4)两点,则m的值为( )A、2 B、8 C、-2 D、-87. 黄金分割数 是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算 ﹣1的值( )A、在1.1和1.2之间 B、在1.2和1.3之间 C、在1.3和1.4之间 D、在1.4和1.5之间8. 如图是成都市某周内日最高气温的折线统计图,关于这7天的日最高气温的说法正确的是( )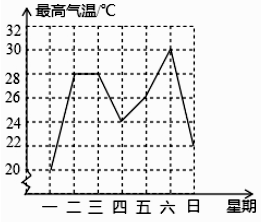 A、极差是8℃ B、众数是28℃ C、中位数是24℃ D、平均数是26℃9. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A、极差是8℃ B、众数是28℃ C、中位数是24℃ D、平均数是26℃9. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A、∠A=∠D B、AB=DC C、∠ACB=∠DBC D、AC=BD10. 如图,在平面直角坐标系中,将△OAB(顶点为网格线交点)绕原点O顺时针旋转90°,得到△OA′B′,若反比例函数y= 的图象经过点A的对应点A′,则k的值为( ) A、-6 B、﹣3 C、3 D、611. 如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是边BC的中点,AD=ED=3,则BC的长为( )
A、-6 B、﹣3 C、3 D、611. 如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是边BC的中点,AD=ED=3,则BC的长为( ) A、3 B、3 C、6 D、612. 如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,BC=3,AC=4,则sin∠ABD的值是( )
A、3 B、3 C、6 D、612. 如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,BC=3,AC=4,则sin∠ABD的值是( )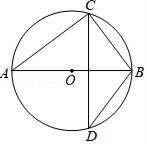 A、 B、 C、 D、13. 已知抛物线 的顶点 关于坐标原点 的对称点为 ,若点 在这条抛物线上,则点 的坐标为( )A、 B、 C、 D、14. 如图,在平行四边形ABCD中,BD⊥AD,以BD为直径作圆,交于AB于E,交CD于F,若BD=12,AD:AB=1:2,则图中阴影部分的面积为( )
A、 B、 C、 D、13. 已知抛物线 的顶点 关于坐标原点 的对称点为 ,若点 在这条抛物线上,则点 的坐标为( )A、 B、 C、 D、14. 如图,在平行四边形ABCD中,BD⊥AD,以BD为直径作圆,交于AB于E,交CD于F,若BD=12,AD:AB=1:2,则图中阴影部分的面积为( )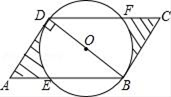 A、12 B、 π C、 D、 π
A、12 B、 π C、 D、 π二、填空题
-
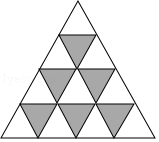
15. 中国古代数学著作《算法统宗》中有这样一段记载:“三百七十八里关,初键步不为难,次日脚痛减一半,六朝才得到其关”其大意是:“有人要去某关口,路程378里,第一天键步行走,第二天起,由于脚痛,每天走的路程都为前一天的一半,一共走了六天才到达目的地,”则此人第六天走的路程为16. 分解因式: .17. 若函数y=x2+2x﹣m的图象与x轴有且只有一个交点,则m的值为.18. 如图是有若干个全等的等边三角形拼成的纸板,若某人向纸板上投掷飞镖,(每次飞镖均落在纸板上),则飞镖落在阴影部分的概率是.
 19. 如图,点M是函数y= x与y= 的图象在第一象限内的交点,OM=4,则k的值为.
19. 如图,点M是函数y= x与y= 的图象在第一象限内的交点,OM=4,则k的值为.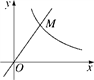 20. 如图,已知菱形 的边 在 轴上,点 的坐标为 ,点 是对角线 上的一个动点,点 在 轴上,当 最短时,点 的坐标为.
20. 如图,已知菱形 的边 在 轴上,点 的坐标为 ,点 是对角线 上的一个动点,点 在 轴上,当 最短时,点 的坐标为.
三、解答题
-
21. 计算: .22. 先化简,再求值: ,其中x= .23. 某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题中选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.
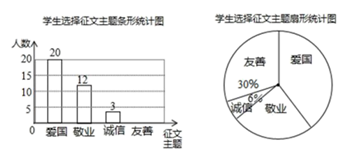 (1)、求本次调查共抽取了多少名学生的征文;(2)、将上面的条形统计图和扇形统计图补充完整;(3)、本次抽取的3份以“诚信”为主题的征文分别是小义、小玉和大力的,若从中随机选取2份以“诚信”为主题的征文进行交流,请用画树状图法或列表法求小义和小玉同学的征文同时被选中的概率.24. 已知:如图,在菱形 中,点 , , 分别为 , , 的中点,连接 , , , .
(1)、求本次调查共抽取了多少名学生的征文;(2)、将上面的条形统计图和扇形统计图补充完整;(3)、本次抽取的3份以“诚信”为主题的征文分别是小义、小玉和大力的,若从中随机选取2份以“诚信”为主题的征文进行交流,请用画树状图法或列表法求小义和小玉同学的征文同时被选中的概率.24. 已知:如图,在菱形 中,点 , , 分别为 , , 的中点,连接 , , , .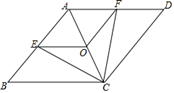 (1)、求证: ;(2)、当 与 满足什么关系时,四边形 是正方形?请说明理由.25. 为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉,经市场调查,甲种花卉的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
(1)、求证: ;(2)、当 与 满足什么关系时,四边形 是正方形?请说明理由.25. 为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉,经市场调查,甲种花卉的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.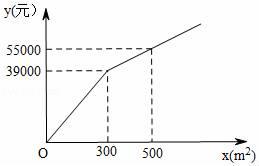 (1)、直接写出当0≤x≤300和x>300时,y与x的函数关系式;(2)、广场上甲、乙两种花卉的种植面积共1200m2 , 若甲种花卉的种植面积不少于200m2 , 且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?26. 如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.
(1)、直接写出当0≤x≤300和x>300时,y与x的函数关系式;(2)、广场上甲、乙两种花卉的种植面积共1200m2 , 若甲种花卉的种植面积不少于200m2 , 且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?26. 如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC. (1)、求证:PC是⊙O的切线;(2)、若∠P=60°,PC=2,求PE的长.27. 如图,直线 与 轴交于点 ,与 轴交于点 ,抛物线 经过 、 两点.
(1)、求证:PC是⊙O的切线;(2)、若∠P=60°,PC=2,求PE的长.27. 如图,直线 与 轴交于点 ,与 轴交于点 ,抛物线 经过 、 两点. (1)、求抛物线的解析式;(2)、如图,点 是直线 上方抛物线上的一动点,当 面积最大时,请求出点 的坐标和 面积的最大值?(3)、在(2)的结论下,过点 作 轴的平行线交直线 于点 ,连接 ,点 是抛物线对称轴上的动点,在抛物线上是否存在点 ,使得以 、 、 、 为顶点的四边形是平行四边形?如果存在,请直接写出点 的坐标;如果不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图,点 是直线 上方抛物线上的一动点,当 面积最大时,请求出点 的坐标和 面积的最大值?(3)、在(2)的结论下,过点 作 轴的平行线交直线 于点 ,连接 ,点 是抛物线对称轴上的动点,在抛物线上是否存在点 ,使得以 、 、 、 为顶点的四边形是平行四边形?如果存在,请直接写出点 的坐标;如果不存在,请说明理由.