甘肃省兰州市2019届九年级中考适应性考试数学试卷(二)
试卷更新日期:2020-01-15 类型:中考模拟
一、单选题
-
1. 9的算术平方根是( )A、 ±3 B、3 C、9 D、±92. 如图是由若干个大小相同的小正方体堆砌而成的几何体,那么其三种视图中周长最小的是( )
 A、主视图 B、左视图 C、俯视图 D、三种一样3. 《语文课程标准》规定:7﹣9年级学生,要求学会制订自己的阅读计划,广泛阅读各种类型的读物,课外阅读总量不少于260万字,每学年阅读两三部名著.那么260万用科学记数法可表示为( )A、26×105 B、2.6×102 C、2.6×106 D、260×1044. 下列标志,是中心对称图形的是( )A、
A、主视图 B、左视图 C、俯视图 D、三种一样3. 《语文课程标准》规定:7﹣9年级学生,要求学会制订自己的阅读计划,广泛阅读各种类型的读物,课外阅读总量不少于260万字,每学年阅读两三部名著.那么260万用科学记数法可表示为( )A、26×105 B、2.6×102 C、2.6×106 D、260×1044. 下列标志,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 如图,将一副三角尺按不同位置摆放,摆放方式中∠α与∠β互余的是( )A、
5. 如图,将一副三角尺按不同位置摆放,摆放方式中∠α与∠β互余的是( )A、 B、
B、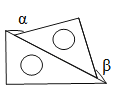 C、
C、 D、
D、 6. 下列运算正确的是( )A、4m﹣m=3 B、a3﹣a2=a C、2xy﹣yx=xy D、a2b﹣ab2=07. 一元一次不等式x+1>2的解在数轴上表示为( )A、
6. 下列运算正确的是( )A、4m﹣m=3 B、a3﹣a2=a C、2xy﹣yx=xy D、a2b﹣ab2=07. 一元一次不等式x+1>2的解在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、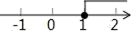 8. 甲车行驶30千米与乙车行驶40千米所用时间相同,已知乙车每小时比甲车多行驶15千米,设甲车的速度为x千米/小时,依据题意列方程正确的是( )A、 B、 C、 D、9. 如图,在平面直角坐标系中,其中一个三角形是由另一个三角形绕某点旋转一定的角度得到的,则其旋转中心是( )
8. 甲车行驶30千米与乙车行驶40千米所用时间相同,已知乙车每小时比甲车多行驶15千米,设甲车的速度为x千米/小时,依据题意列方程正确的是( )A、 B、 C、 D、9. 如图,在平面直角坐标系中,其中一个三角形是由另一个三角形绕某点旋转一定的角度得到的,则其旋转中心是( ) A、(1,0) B、(﹣1,2) C、(0,0) D、(﹣1,1)10. 矩形的两条对角线所成的钝角为120°,若一条对角线的长是2,那么它的周长是( )
A、(1,0) B、(﹣1,2) C、(0,0) D、(﹣1,1)10. 矩形的两条对角线所成的钝角为120°,若一条对角线的长是2,那么它的周长是( )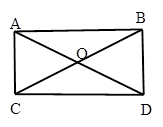 A、6 B、 C、2(1+ ) D、1+11. 如图抛物线y=ax2+bx+c的对称轴为直线x=1,且过点(3,0),下列结论:①abc>0;②a﹣b+c<0;③2a+b>0;④b2﹣4ac>0;正确的有( )个.
A、6 B、 C、2(1+ ) D、1+11. 如图抛物线y=ax2+bx+c的对称轴为直线x=1,且过点(3,0),下列结论:①abc>0;②a﹣b+c<0;③2a+b>0;④b2﹣4ac>0;正确的有( )个.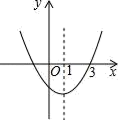 A、1 B、2 C、3 D、412. 如图1,点E为矩形ABCD的边AD上一点,点P从点B出发沿BE→ED→DC运动到点C停止,点Q从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.若点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t之间的函数图象如图2所示.给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②S△ABE=48cm2;③14<t<22时,y=110﹣5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤当△BPQ与△BEA相似时,t=14.5.其中正确结论的序号是( )
A、1 B、2 C、3 D、412. 如图1,点E为矩形ABCD的边AD上一点,点P从点B出发沿BE→ED→DC运动到点C停止,点Q从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.若点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t之间的函数图象如图2所示.给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②S△ABE=48cm2;③14<t<22时,y=110﹣5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤当△BPQ与△BEA相似时,t=14.5.其中正确结论的序号是( ) A、①④⑤ B、①②④ C、①③④ D、①③⑤
A、①④⑤ B、①②④ C、①③④ D、①③⑤二、填空题
-
13. 分解因式:3x2﹣6x2y+3xy2= .14. 在△ABC中,AB=AC,过点A作AD⊥AC交射线CB于点D,若△ABD是等腰三角形,则∠C的大小为度.15. 在函数 的图象上有三个点(﹣2,y1),(﹣1,y2),( ,y3),则y1 , y2 , y3的大小关系为.16. 已知正方形边长为8,黑色部分是以正方形边长为直径的两个半圆,则图中白色部分的面积为(结果保留π).

三、解答题
-
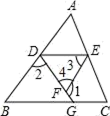
17. 计算:18. 解方程:x2+3x﹣1=0(公式法)19. 先化简,再求值: ,其中 .20. 如图所示,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并对结论进行说理.
 21. 2018年江苏省扬州市初中英语口语听力考试即将举行,某校认真复习,积极迎考,准备了A、B、C、D四份听力材料,它们的难易程度分别是易、中、难、难;a,b是两份口语材料,它们的难易程度分别是易、难.(1)、从四份听力材料中,任选一份是难的听力材料的概率是 .(2)、用树状图或列表法,列出分别从听力、口语材料中随机选一份组成一套完整的模拟试卷的所有情况,并求出两份材料都是难的一套模拟试卷的概率.22. 某服装店用4400元购进A,B两种新式服装,按标价售出后可获得毛利润2800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.
21. 2018年江苏省扬州市初中英语口语听力考试即将举行,某校认真复习,积极迎考,准备了A、B、C、D四份听力材料,它们的难易程度分别是易、中、难、难;a,b是两份口语材料,它们的难易程度分别是易、难.(1)、从四份听力材料中,任选一份是难的听力材料的概率是 .(2)、用树状图或列表法,列出分别从听力、口语材料中随机选一份组成一套完整的模拟试卷的所有情况,并求出两份材料都是难的一套模拟试卷的概率.22. 某服装店用4400元购进A,B两种新式服装,按标价售出后可获得毛利润2800元(毛利润=售价﹣进价),这两种服装的进价,标价如表所示.类型价格
A型
B型
进价(元/件)
60
100
标价(元/件)
100
160
(1)、请利用二元一次方程组求这两种服装各购进的件数;(2)、如果A种服装按标价的9折出售,B种服装按标价的8折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?23. 某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.【收集数据】
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
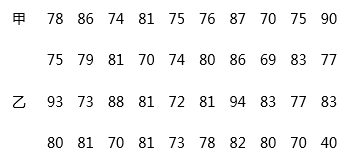
【整理、描述数据】
按如下分数段整理、描述这两组样本数据:
成绩
人数
部门
40≤x≤49
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
甲
0
0
1
11
7
1
乙
(说明:成绩80分及以上为生产技能优秀,70--79分为生产技能良好,60--69分为生产技能合格,60分以下为生产技能不合格)
【分析数据】
两组样本数据的平均数、中位数、众数如下表所示:
部门
平均数
中位数
众数
甲
78.3
77.5
75
乙
78
80.5
81
【得出结论】
.估计乙部门生产技能优秀的员工人数为;
.可以推断出部门员工的生产技能水平较高,理由为.(至少从两个不同的角度说明推断的合理性)
24. 如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长 米,HF长 米,HE长1米. (1)、求篮板底部支架HE与支架AF所成的角∠FHE的度数.(2)、求篮板底部点E到地面的距离.(结果保留根号)25. 如图,已知反比例函数y= 的图象与一次函数y=x+b的图象交于点A(1,4),点B(﹣4,n).
(1)、求篮板底部支架HE与支架AF所成的角∠FHE的度数.(2)、求篮板底部点E到地面的距离.(结果保留根号)25. 如图,已知反比例函数y= 的图象与一次函数y=x+b的图象交于点A(1,4),点B(﹣4,n).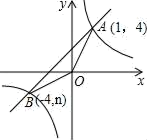 (1)、求n和b的值;(2)、求△OAB的面积;(3)、直接写出一次函数值大于反比例函数值的自变量x的取值范围.26. 如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG
(1)、求n和b的值;(2)、求△OAB的面积;(3)、直接写出一次函数值大于反比例函数值的自变量x的取值范围.26. 如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG (1)、判断CG与⊙O的位置关系,并说明理由;(2)、求证:2OB2=BC•BF;(3)、如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.27. 如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)、判断CG与⊙O的位置关系,并说明理由;(2)、求证:2OB2=BC•BF;(3)、如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.27. 如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.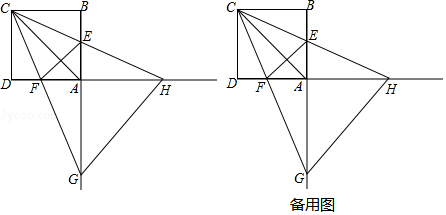 (1)、填空:∠AHC∠ACG;(填“>”或“<”或“=”)(2)、线段AC,AG,AH什么关系?请说明理由;(3)、设AE=m,
(1)、填空:∠AHC∠ACG;(填“>”或“<”或“=”)(2)、线段AC,AG,AH什么关系?请说明理由;(3)、设AE=m,①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.
28. 如图,在平面直角坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),二次函数y= x2+bx﹣2的图象经过C点. (1)、求二次函数的解析式;(2)、平移该二次函数图象的对称轴所在直线l,若直线l恰好将△ABC的面积分为1:2两部分,请求出此时直线l与x轴的交点坐标;(3)、将△ABC以AC所在直线为对称轴翻折180°,得到△AB′C,那么在二次函数图象上是否存在点P,使△PB′C是以B′C为直角边的直角三角形?若存在,请求出P点坐标;若不存在,请说明理由.
(1)、求二次函数的解析式;(2)、平移该二次函数图象的对称轴所在直线l,若直线l恰好将△ABC的面积分为1:2两部分,请求出此时直线l与x轴的交点坐标;(3)、将△ABC以AC所在直线为对称轴翻折180°,得到△AB′C,那么在二次函数图象上是否存在点P,使△PB′C是以B′C为直角边的直角三角形?若存在,请求出P点坐标;若不存在,请说明理由.