甘肃省金昌市永昌县2019年数学中考一模试卷
试卷更新日期:2020-01-15 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、2 B、 C、 D、2. 如图所示的几何体是由5个大小相同的小立方体块搭成,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 将14465000元,用科学记数法表示(保留3个有效数字)( )A、1.45×107 B、1.44×107 C、1.40×107 D、0.145×1084. 不等式组 的解集在数轴上表示正确的是( )A、
3. 将14465000元,用科学记数法表示(保留3个有效数字)( )A、1.45×107 B、1.44×107 C、1.40×107 D、0.145×1084. 不等式组 的解集在数轴上表示正确的是( )A、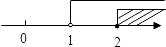 B、
B、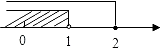 C、
C、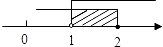 D、
D、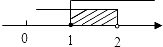 5. 函数y= + 中自变量x的取值范围是( )A、x≤3 B、x<3 C、x≠3 D、x>36. 某天的同一时刻,甲同学测得1m的测竿在地面上的影长为0.6m,乙同学测得国旗旗杆在地面上的影长为9.6m。则国旗旗杆的长为( )A、10m B、12m C、14m D、16m7. 某县为发展教育事业,加强了对教育经费的投入,2008年投入3 000万元,预计2010年投入5 000万元.设教育经费的年平均增长率为x,根据题意,下面所列方程正确的是( )
5. 函数y= + 中自变量x的取值范围是( )A、x≤3 B、x<3 C、x≠3 D、x>36. 某天的同一时刻,甲同学测得1m的测竿在地面上的影长为0.6m,乙同学测得国旗旗杆在地面上的影长为9.6m。则国旗旗杆的长为( )A、10m B、12m C、14m D、16m7. 某县为发展教育事业,加强了对教育经费的投入,2008年投入3 000万元,预计2010年投入5 000万元.设教育经费的年平均增长率为x,根据题意,下面所列方程正确的是( )
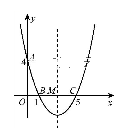
A、3000(1+x)2=5000 B、3000x2=5000 C、3000(1+x%)2=5000 D、3000(1+x)+3000(1+x)2=50008. 如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连结BC.若∠A=36°,则∠C=( ) A、54° B、36° C、27° D、20°9. 点M(-sin60°,cos60°)关于x轴对称的点的坐标是( )A、( , ) B、(- , -) C、(- , ) D、(- , -)10. 已知二次函数 的图象如图所示,现有下列结论:① ;② ;③ ;④ .则其中结论正确的是( )
A、54° B、36° C、27° D、20°9. 点M(-sin60°,cos60°)关于x轴对称的点的坐标是( )A、( , ) B、(- , -) C、(- , ) D、(- , -)10. 已知二次函数 的图象如图所示,现有下列结论:① ;② ;③ ;④ .则其中结论正确的是( )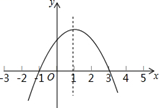 A、①③ B、③④ C、②③ D、①④
A、①③ B、③④ C、②③ D、①④二、填空题
-
11. 分解因式:x3﹣x= .12. 2018年9月某市区一周空气质量报告中其气体污染指数的数据分别是37、39、38、37、39、40、36,这组数据中的中位数是 , 平均数是 , 众数是.13. 方程 ﹣ =3的解是.14. 一元二次方程3x2-x=0的解是.15. 如图,圆弧形桥拱的跨度AB=16米,拱高CD=4米,则拱桥的半径为.
 16. 若关于x的方程mx2﹣4x+2=0有实数根,则m的取值范围是 .17. 若正多边形的一个外角是45°,则该正多边形的边数是 .18. 点(1,y1),(﹣2,y2),(3,y3)均在函数y= 的图象上,则y1 , y2 , y3的大小关系是.
16. 若关于x的方程mx2﹣4x+2=0有实数根,则m的取值范围是 .17. 若正多边形的一个外角是45°,则该正多边形的边数是 .18. 点(1,y1),(﹣2,y2),(3,y3)均在函数y= 的图象上,则y1 , y2 , y3的大小关系是.三、解答题
-
19. 计算 + ;20. 先化简后求值:当 时,求代数式 的值.21. 如图,在Rt△ABC中,∠ACB=90°,AC=1,AB=2,求作:⊙O,使它过点A、B、C(要求:尺规作图,保留作图痕迹,不写作法);
 22. 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
22. 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).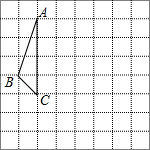 (1)、画出△ABC绕点C顺时针旋转90°后的△A1B1C;(2)、求边AC旋转时所扫过区域的面积.23. 在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)、画出△ABC绕点C顺时针旋转90°后的△A1B1C;(2)、求边AC旋转时所扫过区域的面积.23. 在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止). (1)、请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;(2)、分别求出李燕和刘凯获胜的概率.24. 居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A 非常赞同;B 赞同但要有时间限制;C 无所谓;D 不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.
(1)、请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;(2)、分别求出李燕和刘凯获胜的概率.24. 居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A 非常赞同;B 赞同但要有时间限制;C 无所谓;D 不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.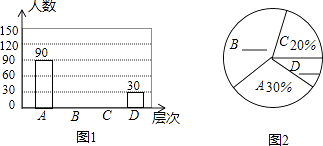
请你根据图中提供的信息解答下列问题:
(1)、求本次被抽查的居民有多少人?
(2)、将图1和图2补充完整;(3)、求图2中“C”层次所在扇形的圆心角的度数;
(4)、估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.
25. 一艘轮船位于灯塔P南偏西60°方向的A处,它向东航行20海里到达灯塔P南偏西45°方向上的B处,若轮船继续沿正东方向航行,求轮船航行途中与灯塔P的最短距离.(结果保留根号)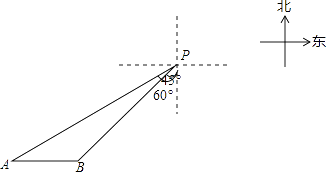 26. 如图,在直角坐标系xOy中,直线 与双曲线 相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
26. 如图,在直角坐标系xOy中,直线 与双曲线 相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1. (1)、求m、n的值;(2)、求直线AC的解析式.
(1)、求m、n的值;(2)、求直线AC的解析式.