辽宁省大连市中山区2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2020-01-15 类型:期末考试
一、单选题
-
1. 2019的相反数是( )A、2019 B、-2019 C、 D、2. 质检员抽查4袋方便面,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数,从轻重的角度看,最接近标准的产品是( )A、-3 B、-1 C、2 D、43. 习近平总书记在庆祝改革开放40周年大会上的讲话提到:40年来,我们始终坚持以经济建设为中心,不断解放发展生产力,我国国内生产总值由3679亿元增长到2017年的827000亿元,其中827000这个数用科学记数法表示为( )A、8.27×103 B、82.7×104 C、8.27×105 D、0.827×1064. 下列图形中可以作为一个三棱柱的展开图的是( )A、
 B、
B、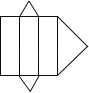 C、
C、 D、
D、 5. 若x=﹣1是关于x的方程2x+5a=3的解,则a的值为( )A、 B、4 C、1 D、﹣16. 下列运算中,正确的是( )A、3a+2b=5ab B、3a2b﹣3ba2=0 C、2a3+3a2=5a5 D、5b2﹣4b2=17. 代数式 与 是同类项,则常数n的值为( )A、2 B、3 C、4 D、68. 有理数 a,b 在数轴上的点的位置如图所示,则正确的结论是( )
5. 若x=﹣1是关于x的方程2x+5a=3的解,则a的值为( )A、 B、4 C、1 D、﹣16. 下列运算中,正确的是( )A、3a+2b=5ab B、3a2b﹣3ba2=0 C、2a3+3a2=5a5 D、5b2﹣4b2=17. 代数式 与 是同类项,则常数n的值为( )A、2 B、3 C、4 D、68. 有理数 a,b 在数轴上的点的位置如图所示,则正确的结论是( ) A、a<﹣4 B、a+ b>0 C、|a|>|b| D、ab>09. 如图,已知直线AB,CD相交于点O,OE平分∠COB,如果∠EOB=55°,那么∠BOD的度数是( )
A、a<﹣4 B、a+ b>0 C、|a|>|b| D、ab>09. 如图,已知直线AB,CD相交于点O,OE平分∠COB,如果∠EOB=55°,那么∠BOD的度数是( )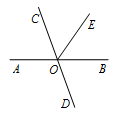 A、35° B、55° C、70° D、110°10. 我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:”一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )A、 =100 B、 =100 C、 D、
A、35° B、55° C、70° D、110°10. 我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:”一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )A、 =100 B、 =100 C、 D、二、填空题
-
11. 的系数是 , 次数是 .12. 30°30′=°.13. 已知∠α和∠β互为补角,且∠β比∠α小20°,则∠β等于.14. 如果 ,那么 的值为.15. 观察下列关于x的单项式,探究其规律:x2 , 3x4 , 5x6 , 7x8 , 9x10 , 11x12 , …,按照上述规律,第2019个单项式是.16. 如图,点C、D为线段AB上两点,AC+BD=a,AD+BC= AB,则CD等于(用含a的式子表示).

三、解答题
-
17. 计算(1)、26﹣(﹣7)+(﹣16)﹣3(2)、6+(﹣2)3×5﹣(﹣3.2)÷418. 解方程:(1)、2(x+3)=5x(2)、 .19. 如图,已知直线l和直线外三点A,B,C,按下列要求画图:
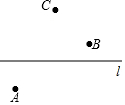
①画射线AB;
②连接BC;
③反向延长BC至D,使得BD=BC;
④在直线l上确定点E,使得AE+CE最小.
20. 先化简,再求值:2(x2y﹣xy2﹣1)﹣(2x2y﹣3xy2﹣3),其中x=2,y=﹣1.21. 解决问题:一辆货车从超市出发,向东走了3千米到达小彬家,继续走2.5千米到达小颖家,然后向西走了10千米到达小明家,最后回到超市.
(1)、以超市为原点,以向东的方向为正方向,用1个单位长度表示1千米,在数轴上表示出小明家,小彬家,小颖家的位置.(2)、小明家距小彬家多远?(3)、货车一共行驶了多少千米?(4)、货车每千米耗油0.2升,这次共耗油多少升?22. 列一元一次方程解应用题某校学生自己动手整修操场,如果让七年级学生单独工作,需要7.5小时完成;如果让八年级学生单独工作,需要5小时完成,如果让七、八年级学生一起工作1小时,再由八年级学生单独完成剩余部分,共需要多少小时完成?
23. 定义一种新运算:观察下列式:1⊙3=1×4+3=7;
3⊙(﹣1)=3×4﹣1=11;
(﹣2)⊙4=(﹣2)×4+4=﹣4;
(﹣3)⊙(﹣5)=(﹣3)×4﹣5=﹣17
……
(1)、请你想一想:a⊙b等于多少;(2)、若a⊙(﹣2b)=4,请计算(﹣3a+2b)⊙(2a﹣3b)的值;(3)、若满足等式(x﹣1)⊙(kx+5)=4(k为整数)中的x为整数,求k的值.24. 为了鼓励市民节约用水,我市居民使用自来水计费方式实施阶梯水价,具体标准见表1,表2分别是小明、小丽、小斌、小宇四家2017年的年用水量和缴纳水费情况.表1:大连市居民自来水实施阶梯水价标准情况:
阶梯
每户年用水量(立方米)
水价(含污水处理费)(元/立方米)
第一阶梯
0~m(含m)
a
第二阶梯
m~240(含240)
4.40
第三阶梯
240以上
7.85
表2:四个家庭2017年的年用水量和缴纳水费情况:
家庭
小明
小丽
小斌
小宇
用水量(立方米)
50
100
200
220
水费(元)
162.5
325
673
761
请你根据表1、表2提供的数据回答下列问题:
(1)、写出表1中的a,m的值;(2)、小颖家2017年使用自来水共缴纳水费827元,则她家2017年的年用水量是多少立方米?25. 如图,∠AOB=α,∠COD=β(α>β),OC与OB重合,OD在∠AOB外,射线OM、ON分别是∠AOC、∠BOD的角平分线.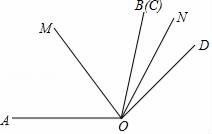 (1)、①若α=100°,β=60°,则∠MON等于多少;
(1)、①若α=100°,β=60°,则∠MON等于多少;②在①的条件下∠COD绕点O逆时针旋转n°(0<n<100(且n≠60)时,求∠MON的度数;
(2)、直接写出∠COD绕点O逆时针旋转n°(0<n<360)时∠MON的值(用含α、β的式子表示).26. 如图1,A、B两点在数轴上对应的数分别为﹣12和4. (1)、直接写出A、B两点之间的距离;(2)、若在数轴上存在一点P,使得AP= PB,求点P表示的数.(3)、如图2,现有动点P、Q,若点P从点A出发,以每秒5个单位长度的速度沿数轴向右运动,同时点Q从点B出发,以每秒2个单位长度的速度沿数轴向左运动,当点Q到达原点O后立即以每秒3个单位长度的速度沿数轴向右运动,求:当OP=4OQ时的运动时间t的值.
(1)、直接写出A、B两点之间的距离;(2)、若在数轴上存在一点P,使得AP= PB,求点P表示的数.(3)、如图2,现有动点P、Q,若点P从点A出发,以每秒5个单位长度的速度沿数轴向右运动,同时点Q从点B出发,以每秒2个单位长度的速度沿数轴向左运动,当点Q到达原点O后立即以每秒3个单位长度的速度沿数轴向右运动,求:当OP=4OQ时的运动时间t的值.