江苏省苏州市张家港市2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2020-01-15 类型:期末考试
一、单选题
-
1. 3的相反数是( )A、﹣3 B、3 C、 D、﹣2. 下列运算正确的是( )A、 B、 C、 D、3. 下列算式中,运算结果为负数的是A、 B、 C、 D、4. 下列关于单项式 的说法中,正确的是( )A、系数是-2,次数是3 B、系数是-2,次数是2 C、系数是 ,次数是3 D、系数是 ,次数是25. 下列四组变形中,属于移项变形的是( )A、由2x-1=0,得x= B、由5x+6=0,得5x=-6 C、由 =2,得x=6 D、由5x=2,得x=6. 如图有一个正方体,它的展开图可能是下面四个展开图中的( )
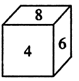 A、
A、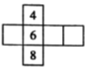 B、
B、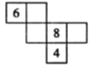 C、
C、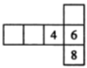 D、
D、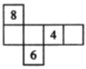 7. 如果一个角的度数为28°14′,那么它的余角的度数为( )A、 B、 C、 D、8. 若代数式 的值与 的值互为相反数,则 的值为( )A、 B、 C、 D、9. 如图,给出如下推理:①∠1=∠3.∴AD∥BC;②∠A+∠1+∠2=180°,∴AB∥CD;③∠A+∠3+∠4=180°,∴AB∥CD;④∠2=∠4,∴AD∥BC其中正确的推理有( )
7. 如果一个角的度数为28°14′,那么它的余角的度数为( )A、 B、 C、 D、8. 若代数式 的值与 的值互为相反数,则 的值为( )A、 B、 C、 D、9. 如图,给出如下推理:①∠1=∠3.∴AD∥BC;②∠A+∠1+∠2=180°,∴AB∥CD;③∠A+∠3+∠4=180°,∴AB∥CD;④∠2=∠4,∴AD∥BC其中正确的推理有( )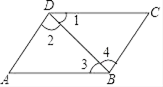 A、①② B、③④ C、①③ D、②④10. 如图,ABCD为一长方形纸带,AB∥CD,将ABCD沿EF折,A,D两点分别与 对应,若∠1=2∠2,则∠AEF的度数为( )
A、①② B、③④ C、①③ D、②④10. 如图,ABCD为一长方形纸带,AB∥CD,将ABCD沿EF折,A,D两点分别与 对应,若∠1=2∠2,则∠AEF的度数为( )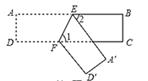 A、60° B、65° C、72° D、75°
A、60° B、65° C、72° D、75°二、填空题
-
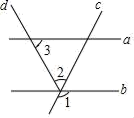
11. 的倒数是.12. 中国的领水面积约为370 000 km2 , 将数370 000用科学记数法表示为:。13. 比较大小:-(-2)-3(填“<”、“=”或“>”)14. 如果单项式xa+1y3与2x2yb-2是同类项,那么a+b=.15. 若x-2y+3=0,则代数式1-2x+4y的值等于.16. 如图,a∥b,∠1=110°,∠3=50°,则∠2的度数是.
 17. 实数a、b在数轴上的位置如图所示,则化简|a+2b|-|a-b|的结果为.
17. 实数a、b在数轴上的位置如图所示,则化简|a+2b|-|a-b|的结果为. 18. 如图,AB=24,点C为AB的中点,点D在线段AC上,且AD:DC=1:2,则DB的长度为.
18. 如图,AB=24,点C为AB的中点,点D在线段AC上,且AD:DC=1:2,则DB的长度为.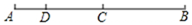
三、解答题
-
19. 计算(1)、12-(-18)+(-7);(2)、12×( - + )(3)、8÷(- )×(-1 )+(-6);(4)、22-(1- )×|3-(-3)2|20. 先化简,再求值: ,其中 .21.(1)、若关于 的方程 的解为2,则 =;(2)、若关于 的方程 和 的解的和为4,求 的值.22. 目前,我市城市居民用电收费方式有以下两种:
普通电价付费方式:全天0. 52元/度;
峰谷电价付费方式:峰时(早8:00~晚21:00)0. 65元/度;谷时(晚21:00~早8:00)0. 40元/度.
(1)、小丽老师家10月份总用电量为280度.①若其中峰时电量为80度,则小丽老师家按照哪种方式付电费比较合适?能省多少元?
②若小丽老师交费137元,那么,小丽老师家峰时电量为多少度?
(2)、到11月份付费时,小丽老师发现11月份总用电量为320度,用峰谷电价付费方式比普通电价付费方式省了18. 4元,那么,11月份小丽老师家峰时电量为多少度?23. 解下列方程:(1)、 ;(2)、 .24. 如图所示,若AB=4.
①延长AB到C,使BC= AB
②在所画图中,如果点D是线段AB的中点,点E是线段BC的中点,那么线段DE的长度是多少?
25. 如图,在9×6的正方形网格中,每个小正方形的顶点都称为格点,点A、B、C都在格点上.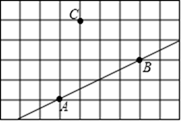
①画射线AC;
②找一格点D,使得直线CD∥AB,画出直线CD;
③找一格点E,使得直线CE⊥AB于点H,画出直线CE,并注明垂足H.(保留作图痕迹,并做好必要的标注)
26. 如图,点D、E在AB上,点F、G分别在BC、CA上,且DG∥BC,∠1=∠2.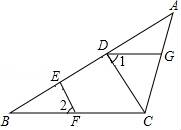 (1)、求证:DC∥EF;(2)、若EF⊥AB,∠1=55°,求∠ADG的度数.27. 已知如图,直线AB、CD相交于点O,∠COE=90°.
(1)、求证:DC∥EF;(2)、若EF⊥AB,∠1=55°,求∠ADG的度数.27. 已知如图,直线AB、CD相交于点O,∠COE=90°. (1)、若∠AOC=36°,求∠BOE的度数;(2)、若∠BOD:∠BOC=1:5,求∠AOE的度数;(3)、在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.28. 已知数轴上三点M,O,N对应的数分别为﹣2,0,4,点P为数轴上任意一点,其对应的数为x.
(1)、若∠AOC=36°,求∠BOE的度数;(2)、若∠BOD:∠BOC=1:5,求∠AOE的度数;(3)、在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.28. 已知数轴上三点M,O,N对应的数分别为﹣2,0,4,点P为数轴上任意一点,其对应的数为x. (1)、如果点P到点M点N的距离相等,则x=.(2)、数轴上是否存在点P,使点P到点M、点N的距离之和是10?若存在,求出x的值;若不存在,请说明理由.(3)、如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.
(1)、如果点P到点M点N的距离相等,则x=.(2)、数轴上是否存在点P,使点P到点M、点N的距离之和是10?若存在,求出x的值;若不存在,请说明理由.(3)、如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时点P到点M、点N的距离相等,求t的值.