湖北省武汉市名校通2018-2019学年七年级上学期数学期末考试试卷
试卷更新日期:2020-01-15 类型:期末考试
一、单选题
-
1. 武汉市江岸区某天的最高气温为5℃,最低气温为-3℃,这天的最高气温与最低气温的温差为( )A、2℃ B、-3℃ C、5℃ D、8℃2. 美国、菲律宾等国不断在中国南海九段线内滋事,中国海军展现了维护中国领海主权的决心和信心,据悉,中国南海九段线以内的所有海域面积约为3120000平方千米,把数3120000用科学记数法表示为( )A、3.12× B、3.12× C、31.2× D、0.312×3. 下列说法中正确的是( )A、- xy的系数是-2,次数是5. B、单项式- 的系数是π,项数是9. C、多项式- +4 +π-2的次数是8,项数是3 D、 是二次四项式4. 如图,A处有一般轮船,B处有一盏灯塔,则在轮船A处看灯塔B的方向是( )
 A、南偏东 B、南偏东 C、西偏北 D、北偏西5. 如图所示的几何体是由五个相同的小正方体组合而成的,从它的正面看到的平面图形是( )
A、南偏东 B、南偏东 C、西偏北 D、北偏西5. 如图所示的几何体是由五个相同的小正方体组合而成的,从它的正面看到的平面图形是( ) A、
A、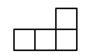 B、
B、 C、
C、 D、
D、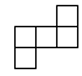 6. 下面哪个图形不是正方体的展开图 ( )A、
6. 下面哪个图形不是正方体的展开图 ( )A、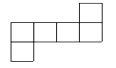 B、
B、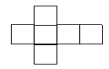 C、
C、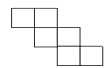 D、
D、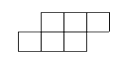 7. 长方形如图折叠,D点折叠到 的位置,已知∠ FC=40°,则∠EFC=( )
7. 长方形如图折叠,D点折叠到 的位置,已知∠ FC=40°,则∠EFC=( ) A、120° B、110° C、105° D、115°8. 如图,线段AB上有C,D两点,以AC,CD,BD为直径的圆的周长分别是 、 、 ,以AB为直径的圆的周长为C,下列结论正确的是( )
A、120° B、110° C、105° D、115°8. 如图,线段AB上有C,D两点,以AC,CD,BD为直径的圆的周长分别是 、 、 ,以AB为直径的圆的周长为C,下列结论正确的是( )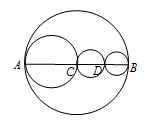 A、 + =C+ B、 + + =C C、 + + >C D、 + + <C9. 孔明灯幼儿园的老师给小朋友们分苹果,如果每人分3个则剩1个,如果每人分4个,则差2个,问有多少苹果?设有x个苹果,则可列方程为( )A、 B、 C、 D、10. 如图,数轴上两定点A、B对应的数分别为-18和14,现在有甲、乙两只电子蚂蚁分别从A、B同时出发,沿着数轴爬行,速度分别为每秒1.5个单位和1.7个单位,它们第一次相向爬行1秒,第二次反向爬行2秒,第三次相向爬行3秒,第四次反向爬行4秒,第五次相向爬行5秒,……,按如此规律,则它们第一次相遇所需的时间为( )
A、 + =C+ B、 + + =C C、 + + >C D、 + + <C9. 孔明灯幼儿园的老师给小朋友们分苹果,如果每人分3个则剩1个,如果每人分4个,则差2个,问有多少苹果?设有x个苹果,则可列方程为( )A、 B、 C、 D、10. 如图,数轴上两定点A、B对应的数分别为-18和14,现在有甲、乙两只电子蚂蚁分别从A、B同时出发,沿着数轴爬行,速度分别为每秒1.5个单位和1.7个单位,它们第一次相向爬行1秒,第二次反向爬行2秒,第三次相向爬行3秒,第四次反向爬行4秒,第五次相向爬行5秒,……,按如此规律,则它们第一次相遇所需的时间为( ) A、55秒 B、190秒 C、200秒 D、210秒
A、55秒 B、190秒 C、200秒 D、210秒二、填空题
-
11. -3的相反数是;-3的倒数是;-3的绝对值是.12. 小明在做解方程的作业时,不小心将方程中的一个常数污染得看不清楚,方程是: ¤.小明翻看了书后的答案,此方程的解是y= ,则这个常数是.13. 已知线段MN,P是MN的中点,Q是PN的中点,R是MQ的中点.若MR=2,则MN=.
 14. 如果一个角的补角比这个角的余角的3倍大10°,则这个角的度数是15. 一列火车匀速行驶,完全通过一条长450米的隧道需要25秒的时间,隧道顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10秒,则火车的速度为米/秒.
14. 如果一个角的补角比这个角的余角的3倍大10°,则这个角的度数是15. 一列火车匀速行驶,完全通过一条长450米的隧道需要25秒的时间,隧道顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10秒,则火车的速度为米/秒.
16. 一般情况下 + = 不成立,但有数可以使得它成立.利润a=b=0.我们称使得 + = 成立的一对数a、b为“相伴数对”,记为(a,b).若(a,2)为“相伴数对”,则a的值为.三、解答题
-
17. 计算:(1)、12-(-12)+(-7)-15(2)、 - - ×18. 先化简,再求值: -2(m- )+(- + ),其中m=-2,n= .19. 解方程:20. 如图,将一幅三角板摆放在一起.
 (1)、∠AOC的度数为 , 射线OA 、OB、OC组成所有小于平角的和为;(2)、反向延长射线OA 到D,OE为∠BOD的平分线,OF为∠COD的平分线,请按题意画出图形,并求出∠EOF的度数.21. 如图,已知线段AB.
(1)、∠AOC的度数为 , 射线OA 、OB、OC组成所有小于平角的和为;(2)、反向延长射线OA 到D,OE为∠BOD的平分线,OF为∠COD的平分线,请按题意画出图形,并求出∠EOF的度数.21. 如图,已知线段AB. (1)、延长线段AB 到C,使BC= AB,D 为AC的中点,请准确画出图形并标出点D;(2)、在(1)的基础上,若DC=2,求AB的长.22. 春节临近,武汉掀起购物狂潮,现有甲、乙、丙三个商场开展的促销活动如下表所示:
(1)、延长线段AB 到C,使BC= AB,D 为AC的中点,请准确画出图形并标出点D;(2)、在(1)的基础上,若DC=2,求AB的长.22. 春节临近,武汉掀起购物狂潮,现有甲、乙、丙三个商场开展的促销活动如下表所示:商场
优惠活动
甲
全场按标价的6折销售
乙
实行“满100元送100元的购物券”的优惠,购物券可以在购买时冲抵现金(比如:某顾客购衣服220元,赠券200元,再购买裤子时可冲抵现金,不再送券)
丙
实行“满100元减50元的优惠”(比如:某顾客购物220元,他只需付款120元)
根据以上活动信息,解决以下问题.
(1)、三个商场同时出售一件标价290元的上衣和一条标价270元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场?完成下表后就可以做出选择;:商场
甲商场
乙商场
丙商场
实际付款(元)
(2)、黄先生发现在甲、乙商场同时出售一件标价380元的上衣和一条标价300多元的裤子,最后付款额也是一样,请问这条裤子的标价是多少元?23. 如图,有两条线段,AB=2(单位长度),CD=1(单位长度)在数轴上运动,点A在数轴上表示的数是-12,点D在数轴上表示的数是15. (1)、点B在数轴上表示的数是 , 点C在数轴上表示的数是 , 线段BC的长=;(2)、若线段AB以1个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动.设运动时间为t秒,当BC=6(单位长度),求t的值;(3)、若线段AB以1个单位长度/秒的速度向左匀速运动,同时线段CD以2个单位长度/秒的速度也向左运动.设运动时间为t秒,当0<t<24时,M为AC中点,N为BD中点,则线段MN的长为.24. 已知,如图1,∠AOB和∠COD共顶点O,OB和OD重合,OM为∠AOD的平分线,ON为∠BOC的平分线,∠AOB=α,∠COD=β.
(1)、点B在数轴上表示的数是 , 点C在数轴上表示的数是 , 线段BC的长=;(2)、若线段AB以1个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动.设运动时间为t秒,当BC=6(单位长度),求t的值;(3)、若线段AB以1个单位长度/秒的速度向左匀速运动,同时线段CD以2个单位长度/秒的速度也向左运动.设运动时间为t秒,当0<t<24时,M为AC中点,N为BD中点,则线段MN的长为.24. 已知,如图1,∠AOB和∠COD共顶点O,OB和OD重合,OM为∠AOD的平分线,ON为∠BOC的平分线,∠AOB=α,∠COD=β.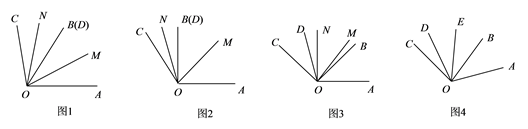 (1)、如图2,若α=90°,β=30°,则∠MON=;(2)、若将∠COD绕O逆时针旋转至图3的位置,求∠MON;(用α,β表示)(3)、如图4,若α=2β,∠COD绕O逆时针旋转,转速为3°/秒,∠AOB绕O同时逆时针旋转,转速为1°/秒(转到OC与OA共线时停止运动),且OE平分∠BOD,请判断∠COE与∠AOD的数量关系并说明理由.
(1)、如图2,若α=90°,β=30°,则∠MON=;(2)、若将∠COD绕O逆时针旋转至图3的位置,求∠MON;(用α,β表示)(3)、如图4,若α=2β,∠COD绕O逆时针旋转,转速为3°/秒,∠AOB绕O同时逆时针旋转,转速为1°/秒(转到OC与OA共线时停止运动),且OE平分∠BOD,请判断∠COE与∠AOD的数量关系并说明理由.