辽宁省辽阳市2019届九年级上学期数学期末考试试卷
试卷更新日期:2020-01-15 类型:期末考试
一、单选题
-
1. 下列物体的左视图是圆的是( )A、
 足球
B、
足球
B、 水杯
C、
水杯
C、 圣诞帽
D、
圣诞帽
D、 鱼缸
2. 用配方法解方程: ,下列配方正确的是( )A、 B、 C、 D、3. 关于x的一元二次方程kx2+3x﹣1=0有实数根,则k的取值范围是( )A、k≤﹣ B、k≤﹣ 且k≠0 C、k≥﹣ D、k≥﹣ 且k≠04. 下列命题正确的是( )A、一组对边相等,另一组对边平行的四边形是平行四边形 B、对角线相互垂直的四边形是菱形 C、对角线相等的四边形是矩形 D、对角线相互垂直平分且相等的四边形是正方形5. 如图所示,在正方形ABCD中,E是AC上的一点,且 ,则 的度数是( )
鱼缸
2. 用配方法解方程: ,下列配方正确的是( )A、 B、 C、 D、3. 关于x的一元二次方程kx2+3x﹣1=0有实数根,则k的取值范围是( )A、k≤﹣ B、k≤﹣ 且k≠0 C、k≥﹣ D、k≥﹣ 且k≠04. 下列命题正确的是( )A、一组对边相等,另一组对边平行的四边形是平行四边形 B、对角线相互垂直的四边形是菱形 C、对角线相等的四边形是矩形 D、对角线相互垂直平分且相等的四边形是正方形5. 如图所示,在正方形ABCD中,E是AC上的一点,且 ,则 的度数是( ) A、45度 B、30度 C、 度 D、20度6. 在同一天的四个不同时刻,某学校旗杆的影子如图所示,按时间先后顺序排列的是( )
A、45度 B、30度 C、 度 D、20度6. 在同一天的四个不同时刻,某学校旗杆的影子如图所示,按时间先后顺序排列的是( )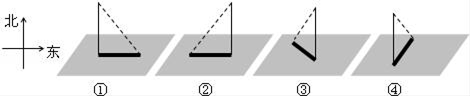 A、①②③④ B、②③④① C、③④①② D、④③①②7. 在同一直角坐标系中,函数 与y=ax+1(a≠0)的图象可能是( )A、
A、①②③④ B、②③④① C、③④①② D、④③①②7. 在同一直角坐标系中,函数 与y=ax+1(a≠0)的图象可能是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,在平行四边形ABCD中,E为CD上一点,连接AE,BE,BD,且AE,BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
8. 如图,在平行四边形ABCD中,E为CD上一点,连接AE,BE,BD,且AE,BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( ) A、2:3 B、2:5 C、3:5 D、3:29. 如图,四边形ABCD是轴对称图形,且直线AC是否对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中结论正确的序号是( )
A、2:3 B、2:5 C、3:5 D、3:29. 如图,四边形ABCD是轴对称图形,且直线AC是否对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中结论正确的序号是( )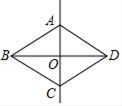 A、①②③ B、①②③④ C、②③④ D、①③④10. 如图,菱形ABCD的边AD与x轴平行,A,B两点的横坐标分别为1和3,反比例函数y= 的图象经过A,B两点,则菱形ABCD的面积是( )
A、①②③ B、①②③④ C、②③④ D、①③④10. 如图,菱形ABCD的边AD与x轴平行,A,B两点的横坐标分别为1和3,反比例函数y= 的图象经过A,B两点,则菱形ABCD的面积是( )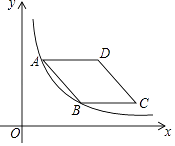 A、4 B、4 C、2 D、2
A、4 B、4 C、2 D、2二、填空题
-
11. 一元二次方程x2-4x+1=0的两根是x1 , x2 , 则x1•x2的值是.12. 已知 ,且3a-2b+c=9,则2a+4b-3c=.13.
如图,以点O为位似中心,将△ABC放大得到△DEF,若AD=OA,则△ABC与△DEF的面积之比为 .
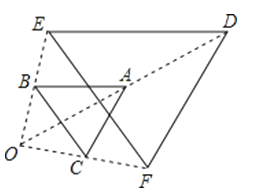 14. 如图,小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m、与旗杆相距22m,则旗杆的高为.
14. 如图,小东用长为3.2m的竹竿做测量工具测量学校旗杆的高度,移动竹竿,使竹竿、旗杆顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距8m、与旗杆相距22m,则旗杆的高为. 15. 相邻两边长的比值是黄金分割数的矩形,叫做黄金矩形,从外形看,它最具美感.现在想要制作一张“黄金矩形”的贺年卡,如果较长的一条边长等于20厘米,那么相邻一条边的边长等于厘米.16. 如图,点A(3,n)在双曲线y= 上,过点A作 AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点B,则△ABC周长的值是.
15. 相邻两边长的比值是黄金分割数的矩形,叫做黄金矩形,从外形看,它最具美感.现在想要制作一张“黄金矩形”的贺年卡,如果较长的一条边长等于20厘米,那么相邻一条边的边长等于厘米.16. 如图,点A(3,n)在双曲线y= 上,过点A作 AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点B,则△ABC周长的值是. 17. 分解因式: =18. 如图,n个边长为1的相邻正方形的一边均在同一直线上,点M1 , M2 , M3 , …Mn分别为边B1B2 , B2B3 , B3B4 , …,BnBn+1的中点,△B1C1M1的面积为S1 , △B2C2M2的面积为S2 , …△Bn∁nMn的面积为Sn , 则Sn=.(用含n的式子表示)
17. 分解因式: =18. 如图,n个边长为1的相邻正方形的一边均在同一直线上,点M1 , M2 , M3 , …Mn分别为边B1B2 , B2B3 , B3B4 , …,BnBn+1的中点,△B1C1M1的面积为S1 , △B2C2M2的面积为S2 , …△Bn∁nMn的面积为Sn , 则Sn=.(用含n的式子表示)
三、解答题
-
19. 先化简,再求值:(1﹣x+ )÷ ,其中x=tan45°+( )﹣1 .20. 解方程:21. 广安市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.(1)、求平均每次下调的百分率.(2)、某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?22. 一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。(1)、从箱子中任意摸出一个球是白球的概率是多少?(2)、从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。23. 如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
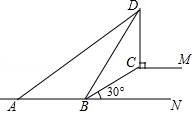 (1)、求灯杆CD的高度;(2)、求AB的长度(结果精确到0.1米).(参考数据: =1.73.sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)24. 如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)、求灯杆CD的高度;(2)、求AB的长度(结果精确到0.1米).(参考数据: =1.73.sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)24. 如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.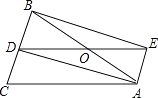 (1)、求证:四边形AEBD是矩形;(2)、当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由25. 如图,已知矩形OABC中,OA=2,AB=4,双曲线 (k>0)与矩形两边AB、BC分别交于E、F.
(1)、求证:四边形AEBD是矩形;(2)、当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由25. 如图,已知矩形OABC中,OA=2,AB=4,双曲线 (k>0)与矩形两边AB、BC分别交于E、F. (1)、若E是AB的中点,求F点的坐标;(2)、若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,证明△EGD∽△DCF,并求k的值.26. 如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.
(1)、若E是AB的中点,求F点的坐标;(2)、若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,证明△EGD∽△DCF,并求k的值.26. 如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.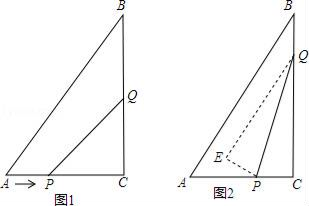 (1)、当t=2时,求线段PQ的长度;(2)、当t为何值时,△PCQ的面积等于5cm2?(3)、在P、Q运动过程中,在某一时刻,若将△PQC翻折,得到△EPQ,如图2,PE与AB能否垂直?若能,求出相应的t值;若不能,请说明理由.
(1)、当t=2时,求线段PQ的长度;(2)、当t为何值时,△PCQ的面积等于5cm2?(3)、在P、Q运动过程中,在某一时刻,若将△PQC翻折,得到△EPQ,如图2,PE与AB能否垂直?若能,求出相应的t值;若不能,请说明理由.