辽宁省丹东市2019届九年级上学期数学期末考试试卷
试卷更新日期：2020-01-15 类型：期末考试
一、单选题
-
1. 一元二次方程2x2+3x﹣5＝0的常数项是（ ）A、﹣5 B、2 C、3 D、52. 下列几何体中，主视图和俯视图都为矩形的是（ ）A、
B、
C、
D、
3. 如图，EF过矩形ABCD对角线的交点O，且分别交AB，CD于E，F，矩形ABCD内的一个动点P落在阴影部分的概率是（ ）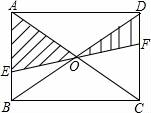
A、 B、 C、 D、4. 下列关于矩形的说法，正确的是（ ）．A、对角线相等的四边形是矩形 B、对角线互相平分的四边形是矩形 C、矩形的对角线互相垂直且平分 D、矩形的对角线相等且互相平分5. 如图，正方形ABCD中，E为AB中点，BC＝4BF，那么图中与△ADE相似的三角形有（ ）
A、△CDF B、△BEF C、△BEF、△DCF D、△BEF，△EDF6. 已知一个菱形的周长是 ， 两条对角线的比是4：3，则这个菱形的面积是（ ）
A、 B、 C、 D、7. 据有关实验测定，当室温与人体正常体温（37℃）的比值为黄金比时，人体感到最舒适，这个室温约（精确到1℃）（ ）A、21℃ B、22℃ C、23℃ D、24℃8. 已知一次函数y＝kx﹣1和反比例函数y＝ ，则这两个函数在同一平面直角坐标系中的图象可能是（ ）A、
B、
C、
D、
9. 如图，平行四边形ABCD中，对角线AC，BD相交于点O，BD＝2AD，E，F，G分别是OC，OD，AB的中点，下列结论：①BE⊥AC；②EG＝EF；③△EFG≌△GBE；④EA平分∠GEF；⑤四边形BEFG是菱形.其中正确的个数是（ ）
A、2 B、3 C、4 D、5二、填空题
-
10. 已知关于 的一元二次方程 有两个相等的实数根，则 的值是 ．
11. 反比例函数y＝ 的图象，当x＞0时，y随x的增大而增大，则k的取值范围是.12. 某小区2010年屋顶绿化面积为2000平方米，计划2012年屋顶绿化面积要达到2880平方米.如果每年屋顶绿化面积的增长率相同，那么这个增长率是.13. 已知==≠0，则的值为
14. 如图，矩形ABCD的对角线AC与BD相交于点O，∠ADB＝30°，AB＝4，则矩形ABCD的面积为.
15. 一个口袋里有相同的红、绿、黄三种颜色的小球，其中有6个红球，5个绿球.若任意摸出一个绿球的概率是 ，则任意摸出一个黄球的概率是.16. 如图，在2×3的方格纸中，每个小正方形的边长均为1，点A，B，C，D都在格点上，AB与CD交于点E，则EB的长为.
17. 如图，在平面直角坐标系中，已知点A(2，4)，B(6，﹣2)，以原点O为位似中心，相似比为 ，把△ABO缩小，则点A的对应点A′的坐标是.
18. 如图，已知动点A在反比例函数y＝ (x＞0)的图象上，直线PQ与x轴，y轴交于P、Q两点，过点A作CD∥x轴，交y轴于点C，交直线PQ于点D，过点A作EB∥y轴交x轴于点B，交直线PQ于点E，若CE∥BD且CA：AE＝1：2，QE：DP＝1：9，则阴影部分的面积为.
三、解答题
-
19. 解方程：2x2﹣4x﹣1＝0(用配方法)20. 如图所示，请画出这个几何体的三视图.
21. 如图，在▱ABCD，点O是边BC的中点，连接DO并延长，交AB的延长线于点E，连接BD、EC.
(1)、求证：四边形BECD是平行四边形；(2)、若∠BOD＝100°，则当∠A＝时，四边形BECD是矩形.22. 我市某旅行社为吸引我市市民组团去长白山风景区旅游，推出了如下的收费标准：如果人数不超过25人，人均旅游费用为800元；如果人数超过25人，每增加1人，人均旅游费用降低20元，但人均旅游费用不得低于650元，某单位组织员工去长白山风景区旅游，共支付给旅行社旅游费用21000元，请问该单位这次共有多少员工去长白山风景区旅游？23. 随着信息技术的迅猛发展，人们去商场购物的支付方式更加多样、便捷，在一次购物中，张华和李红都想从“微信”、“支付宝”、“银行卡”、“现金”四种支付方式中选一种方式进行支付.(1)、张华用“微信”支付的概率是.(2)、请用画树状图或列表法求出两人恰好选择同一种支付方式的概率.(其中“微信”、“支付宝”、“银行卡”、“现金”分别用字母“A”“B”“C”“D”代替)24. 甲和乙两位同学想测量一下广场中央的照明灯P的高度，如图，当甲站在A处时，乙测得甲的影子长AD正好与他的身高AM相等，接着甲沿AC方向继续向前走，走到点B处时，甲的影子刚好是线段AB，此时测得AB的长为1.2m.已知甲直立时的身高为1.8m，求照明灯的高CP的长.
25. 如图，A(8，6)是反比例函数y＝ (x＞0)在第一象限图象上一点，连接OA，过A作AB∥x轴，且AB＝OA(B在A右侧)，直线OB交反比例函数y＝ 的图象于点M
(1)、求反比例函数y＝ 的表达式；(2)、求点M的坐标；(3)、设直线AM关系式为y＝nx+b，观察图象，请直接写出不等式nx+b﹣ ≤0的解集.26. 如图1，AC是边长为6的菱形ABCD的对角线，∠ABC＝∠PAQ＝60°，∠PAQ绕点A旋转，射线AP、AQ分别交边BC、CD于点E、F，连接EF.请探究：
(1)、在旋转过程中，线段AE、AF有怎样的数量关系？并说明理由；(2)、在旋转过程中，△AEF的面积是否存在最小值？若存在，请求出最小值，若不存在，请说明理由(3)、如图2，将∠PAQ沿着AC向下平移至点A处，使CA′：AA′＝2：1，在∠PA′Q绕点A′旋转过程中，始终保持∠ABC＝∠PA′Q，射线A′P、A′Q分别交直线BC、CD于点E、F，连接EF.当S△A′EF：S菱形ABCD＝19：18时，直接写出线段CE的长.