辽宁省大连市西岗区2019届九年级上学期数学期末考试试卷
试卷更新日期:2020-01-15 类型:期末考试
一、单选题
-
1. 下面数学符号,既是轴对称图形,又是中心对称图形的是( )A、
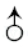 B、
B、 C、
C、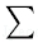 D、
D、 2. 抛物线 的顶点坐标是( )A、(﹣1,2) B、(﹣1,﹣2) C、(1,﹣2) D、(1,2)3. 在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值为( )A、 B、 C、 D、4. 如图,A、B、C是⊙O上的三点,且∠ABC=70°,则∠AOC的度数是( )
2. 抛物线 的顶点坐标是( )A、(﹣1,2) B、(﹣1,﹣2) C、(1,﹣2) D、(1,2)3. 在Rt△ABC中,∠C=90°,AB=5,AC=4,则sinA的值为( )A、 B、 C、 D、4. 如图,A、B、C是⊙O上的三点,且∠ABC=70°,则∠AOC的度数是( )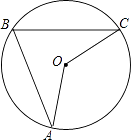 A、35° B、140° C、70° D、70°或 140°5. 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6, ,则EC的长是( )
A、35° B、140° C、70° D、70°或 140°5. 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6, ,则EC的长是( ) A、4.5 B、8 C、10.5 D、146. 已知扇形的弧长为3πcm,半径为6cm,则此扇形的圆心角为( )A、30° B、45° C、60° D、90°7. 已知甲、乙两地相距20千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )A、t=20v B、t= C、t= D、t=8. 如图,P(x,y)是反比例函数y= 的图象在第一象限分支上的一个动点,PA⊥x轴于点A,PB⊥y轴于点B,随着自变量x的增大,矩形OAPB的面积( )
A、4.5 B、8 C、10.5 D、146. 已知扇形的弧长为3πcm,半径为6cm,则此扇形的圆心角为( )A、30° B、45° C、60° D、90°7. 已知甲、乙两地相距20千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )A、t=20v B、t= C、t= D、t=8. 如图,P(x,y)是反比例函数y= 的图象在第一象限分支上的一个动点,PA⊥x轴于点A,PB⊥y轴于点B,随着自变量x的增大,矩形OAPB的面积( ) A、不变 B、增大 C、减小 D、无法确定9. 中国“一带一路”倡议给沿线国家和地区带来很大的经济效益,沿线某地区居民2016年年收入300美元,预计2018年年收入将达到1500美元,设2016年到2018年该地区居民年人均收入平均增长率为x,可列方程为( )A、300(1+x)2=1500 B、300(1+2x)=1500 C、300(1+x2)=1500 D、300+2x=150010. 已知:二次函数y=ax2+bx+c图象上部分点的横坐标x与纵坐标y的对应值如表格所示:
A、不变 B、增大 C、减小 D、无法确定9. 中国“一带一路”倡议给沿线国家和地区带来很大的经济效益,沿线某地区居民2016年年收入300美元,预计2018年年收入将达到1500美元,设2016年到2018年该地区居民年人均收入平均增长率为x,可列方程为( )A、300(1+x)2=1500 B、300(1+2x)=1500 C、300(1+x2)=1500 D、300+2x=150010. 已知:二次函数y=ax2+bx+c图象上部分点的横坐标x与纵坐标y的对应值如表格所示:x
…
﹣1
0
1
2
…
y
…
0
3
4
3
…
那么它的图象与x轴的另一个交点坐标是( )
A、(1,4) B、(2,0) C、(3,0) D、(4,0)二、填空题
-
11. 函数y=- 的自变量的取值范围是.12. 如图,⊙O的半径OA等于5,半径OC与弦AB垂直,垂足为D,若OD=3,则弦AB的长为.
 13. 点A(1,6)、B(2,n)都在反比例函数y= 的图象上,则n的值为.14. 如图,△ABC中,D、E分别是AB、AC上的点(DE不平行BC),若使△ADE与△ABC相似,则需要添加即可(只需添加一个条件).
13. 点A(1,6)、B(2,n)都在反比例函数y= 的图象上,则n的值为.14. 如图,△ABC中,D、E分别是AB、AC上的点(DE不平行BC),若使△ADE与△ABC相似,则需要添加即可(只需添加一个条件). 15. 如图,把△ABC绕点C顺时针旋转得到△A′B′C,此时A′B′⊥AC于D,已知∠A=51°,则∠B′CB的度数是.
15. 如图,把△ABC绕点C顺时针旋转得到△A′B′C,此时A′B′⊥AC于D,已知∠A=51°,则∠B′CB的度数是. 16. 如图,已知双曲线y= (k>0)经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k=.
16. 如图,已知双曲线y= (k>0)经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k=.
三、解答题
-
17.(1)、解方程:x2+4x﹣5=0(2)、 +( )﹣1﹣2cos30°+(2﹣π)018. 如图,已知等腰三角形ADC,AD=AC,B是线段DC上的一点,连结AB,且有AB=DB.
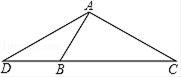 (1)、求证:△ADB∽△CDA;(2)、若DB=2,BC=3,求AD的值.19. 如图,建筑物的高CD为17.32米,在其楼顶C,测得旗杆底部B的俯角α为60°,旗杆顶部A的仰角β为30°,请你计算旗杆的高度.( ≈1.732,结果精确到0.1米)
(1)、求证:△ADB∽△CDA;(2)、若DB=2,BC=3,求AD的值.19. 如图,建筑物的高CD为17.32米,在其楼顶C,测得旗杆底部B的俯角α为60°,旗杆顶部A的仰角β为30°,请你计算旗杆的高度.( ≈1.732,结果精确到0.1米) 20. 某工厂大门是一抛物线形水泥建筑物(如图),大门地面宽AB=4米,顶部C离地面高度为4.4米.现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8米,装货宽度为2.4米.请通过计算,判断这辆汽车能否顺利通过大门?
20. 某工厂大门是一抛物线形水泥建筑物(如图),大门地面宽AB=4米,顶部C离地面高度为4.4米.现有一辆满载货物的汽车欲通过大门,货物顶部距地面2.8米,装货宽度为2.4米.请通过计算,判断这辆汽车能否顺利通过大门?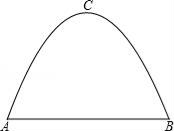 21. 如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与y轴相交于点A,与反比例函数y2= (k≠0)的图象相交于点B(3,2)、C(﹣1,n).
21. 如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与y轴相交于点A,与反比例函数y2= (k≠0)的图象相交于点B(3,2)、C(﹣1,n). (1)、求一次函数和反比例函数的解析式;(2)、根据图象,直接写出y1>y2时x的取值范围.22. 【发现】x4﹣5x2+4=0是一个一元四次方程.(1)、【探索】根据该方程的特点,通常用“换元法”解方程:
(1)、求一次函数和反比例函数的解析式;(2)、根据图象,直接写出y1>y2时x的取值范围.22. 【发现】x4﹣5x2+4=0是一个一元四次方程.(1)、【探索】根据该方程的特点,通常用“换元法”解方程:设x2=y,那么x4=y2 , 于是原方程可变为.
解得:y1=1,y2=.
当y=1时,x2=1,∴x=±1;
当y=时,x2= , ∴x=;
原方程有4个根,分别是.
(2)、【应用】仿照上面的解题过程,求解方程: .23. 如图,在△ABC中,∠C=90°,点O为BE上一点,以OB为半径的⊙O交AB于点E,交AC于点D.BD平分∠ABC. (1)、求证:AC为⊙O切线;(2)、点F为 的中点,连接BF,若BC= ,BD=8,求⊙O半径及DF的长.24. 如图1,在四边形ABCD中,AB∥CD,BC⊥CD,过点C作CE⊥AD于点E,CE=4,△CDE沿射线DA平移,当CE经过点B时,运动停止.设点D的平移距离为x,平移后的三角形与四边形ABCD的重合部分面积为y,y与x的函数图象如图2所示:
(1)、求证:AC为⊙O切线;(2)、点F为 的中点,连接BF,若BC= ,BD=8,求⊙O半径及DF的长.24. 如图1,在四边形ABCD中,AB∥CD,BC⊥CD,过点C作CE⊥AD于点E,CE=4,△CDE沿射线DA平移,当CE经过点B时,运动停止.设点D的平移距离为x,平移后的三角形与四边形ABCD的重合部分面积为y,y与x的函数图象如图2所示: (1)、图中DE=;(2)、求BC的长;(3)、求y与x的函数关系式,并直接写出x的取值范围.25. 阅读下面材料:
(1)、图中DE=;(2)、求BC的长;(3)、求y与x的函数关系式,并直接写出x的取值范围.25. 阅读下面材料:小明遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,AC=BC,在三角形内取一点D,AD=AC,∠CAD=30°,求∠ADB.
小明通过探究发现,∠DAB=∠DCB=15°,BC=AD,这样就具备了一边一角的图形特征,他果断延长CD至点E,使CE=AB,连接EB,造出全等三角形,使问题得到解决.
 (1)、按照小明思路完成解答,求∠ADB;(2)、参考小明思考问题的方法,解答下列问题:
(1)、按照小明思路完成解答,求∠ADB;(2)、参考小明思考问题的方法,解答下列问题:如图2,△ABC中,AB=AC,点D、E、F分别为BC、AC、AB上一点,连接DE,延长FE、DF分别交BC、CA延长线于点G、H,若∠DHC=∠EDG=2∠G.
①在图中找出与∠DEC相等的角,并加以证明;
②若BG=kCD,猜想DE与DG的数量关系并证明.
26. 在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,顶点为D,且过点(2,﹣3a).(1)、求抛物线的解析式;(2)、抛物线上是否存在一点P,过点P作PM⊥BD,垂足为点M,PM=2DM?若存在,求点P的坐标;若不存在,说明理由.(3)、在(2)的条件下,求△PMD的面积.