吉林省长春市名校调研2018-2019学年七年级下学期数学第三次月考试卷

试卷更新日期：2020-01-15 类型：月考试卷

进入出卷网下载

一、单选题

1. 现有两根小木棒，它们的长度分别为 $4 c m$ 和 $5 c m$ ，若要钉成一个三角形架，下列长度不可以作为第三根木棒长度的是（）

A、 $4 c m$ B、 $5 c m$ C、 $8 c m$ D、 $10 c m$

查看试题解析
2. 已知两个不等式的解集在数轴上如图所示，则由这两个不等式组成的不等式组的解集为（）

A、 $- 2 < x < 2$ B、 $x < 2$ C、 $x \geq - 2$ D、 $x > 2$

查看试题解析
3. $n$ 边形的内角和等于 $1080 °$ ，则 $n$ 的值是（）

A、8 B、7 C、6 D、5

查看试题解析
4. 方程组 ${\begin{array}{l} 2 x + y = ■ \\ x + y = 3 \end{array}$ 的解为 ${\begin{array}{l} x = 2 \\ y = ■ \end{array}$ ，则被遮盖的前后两个数分别为（）

A、1、2 B、1、5 C、5、1 D、2、4

查看试题解析
5. 若 $3 m - 7$ 和 $9 - m$ 互为相反数，则 $m$ 的值是（）

A、4 B、1 C、 $- 1$ D、 $- 4$

查看试题解析
6. 用一批相同的正多边形地砖辅地，要求顶点聚在一起，且砖与砖之间不留空隙，这样的地砖是（）

A、正五边形 B、正三角形，正五边形 C、正三角形，正五边形，正六边形 D、正三角形，正方形，正六边形

查看试题解析
7. 已知关于x的不等式组 ${\begin{array}{l} 3 x - 1 ≺ 4 (x - 1) \\ x ≺ m \end{array}$ 无解，则m的取值范围是（）

A、m≤3 B、m＞3 C、m＜3 D、m≥3

查看试题解析
8. 某种服装的进价为240元，出售时标价为360元，由于换季，商店准备打折销售，但要保特利润不低20%，那么至多打（）

A、6折 B、7折 C、8折 D、9折

查看试题解析

二、填空题

9. 我们用如图的方法（斜钉上一块木条）来修理一条摇晃的凳子的数学原理是利用三角形的.

查看试题解析
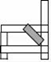10. 当代数式2x﹣2与3+x的值相等时，x＝．

查看试题解析
11. 若 ${\begin{array}{l} x + y = 5 \\ 3 x - 5 y = 7 \end{array}$ ，则 $x - y =$ ．

查看试题解析
12. 从一个多边形的某顶点出发，连接其余各顶点，把该多边形分成了4个三角形，则这个多边形是边形.

查看试题解析
13. 关于 $x$ 的不等式 $- 2 x - 4 \leq 3$ 的所有负整数解的和是.

查看试题解析
14. 如图，△ABC是一块直角三角板，∠BAC＝90°，∠B＝25°，现将三角板叠放在一把直尺上，使得点A落在直尺的一边上，AB与直尺的另一边交于点D，BC与直尺的两边分别交于点E，F，若∠CAF＝20°，则∠BED的度数为°．

查看试题解析

三、解答题

15. 解方程：x+ $\frac{1}{2}$ ＝ $\frac{2 - x}{3}$

查看试题解析
16. 已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} 2 x + y = 1 + 3 m \\ x + 2 y = 1 - m \end{array}$ 的解满足 $x + y < 0$ ，求 $m$ 的取值范围．

查看试题解析
17. 求不等式组 ${\begin{array}{l} 1 - 2 x < 3 \\ \frac{x + 1}{3} < 2 \end{array}$ 的整数解．

查看试题解析
18. 一个多边形的每个内角都相等，并且其中一个内角比它相邻的外角大 $100 °$ ，求这个多边形的边数．

查看试题解析
19. 如图，在 $Δ A B C$ 中， $A D$ 是 $B C$ 边上的中线， $Δ A D C$ 的周长比 $Δ A B D$ 的周长多 $5 c m$ ， $A B$ 与 $A C$ 的和为 $11 c m$ ，求 $A C$ 的长．

查看试题解析
20. 随着中国传统节日“端午节”的临近，永旺超市决定开展“欢度端午，回馈顾客”的让利促销活动，对部分品牌粽子进行打折销售，其中甲品牌粽子打八折，乙品牌粽子打七五折．已知打折前，买1盒甲品牌粽子和2盒乙品牌粽子需230元；打折后，买50盒甲品牌粽子和40盒乙品牌粽子需要5200元．

(1)、打折前甲、乙两种品牌粽子每盒分别为多少元？

(2)、阳光敬老院需购买甲品牌粽子80盒，乙品牌粽子100盒，问打折后购买这批粽子比不打折节省了多少钱？

查看试题解析
21. 定义一种法则“⊕”如下：a⊕b＝ ${\begin{array}{l} a (a > b) \\ b (a ⩽ b) \end{array}$ ，例如：1⊕2＝2．

(1)、（﹣2018）⊕（﹣2019）＝；

(2)、若（﹣3p+5）⊕8＝8，求p的负整数值．

查看试题解析
22. 已知直线 $P Q / / M N$ ， $Δ A B C$ 的顶点 $A$ 与 $B$ 分别在直线 $M N$ 与 $P Q$ 上， $∠ C = 45 °$ ，设 $∠ C B Q = ∠ a$ ， $∠ C A N = ∠ β$ ．

(1)、如图①，当点 $C$ 落在 $P Q$ 的上方时， $A C$ 与 $P Q$ 相交于点 $D$ ，求证： $∠ β = ∠ a + 45 °$ ；

(2)、如图②．当点 $C$ 落在直线 $M N$ 的下方时， $B C$ 与 $M N$ 交于点 $F$ ，请判断 $∠ a$ 与 $∠ β$ 的数量关系，并说明理由．

查看试题解析
23. 某公司有A、B两种型号的客车，它们的载客量、每天的租金如表所示：

A型号客车

B型号客车

载客量(人/辆)

45

30

租金(元/辆)

600

450

已知某中学计划租用A、B两种型号的客车共10辆，同时送七年级师生到沙家参加社会实践活动，已知该中学租车的总费用不超过5600元．

(1)、求最多能租用多少辆A型号客车？

(2)、若七年级的师生共有380人，请写出所有可能的租车方案．

查看试题解析
24. 探究与发现：

(1)、探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？

已知：如图1，∠FDC与∠ECD分别为△ADC的两个外角，试探究∠A与∠FDC+∠ECD的数量关系．

(2)、探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？

已知：如图2，在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系．

(3)、探究三：若将△ADC改为任意四边形ABCD呢？

已知：如图3，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．

查看试题解析

	A型号客车	B型号客车
载客量(人/辆)	45	30
租金(元/辆)	600	450