辽宁省昌图县2019届九年级上学期数学期末考试试卷

试卷更新日期：2020-01-15 类型：期末考试

进入出卷网下载

一、单选题

1. 正方形具有而菱形不具有的性质是（）

A、四边相等 B、四角相等 C、对角线互相平分 D、对角线互相垂直

查看试题解析
2. 下列各组图形一定相似的是（）。

A、任意两个平行四边形 B、任意两个矩形 C、任意两个菱形 D、任意两个正方形

查看试题解析
3. 等腰直角三角形斜边与斜边上的高的比是（）

A、1：2 B、2：1 C、1： $\sqrt{3}$ D、 $\sqrt{3}$ ：1

查看试题解析
4. 已知 $△ ABC$ 的三边长分别为 $7.5$ ，9和 $10.5$ ， $△ DEF$ 的一边长为5，当 $△ DEF$ 的另两边长是下列哪一组时，这两个三角形相似（）

A、4，5 B、5，6 C、6，7 D、7，8

查看试题解析
5. 一条线段的黄金分割点有（）

A、1个 B、2个 C、3个 D、无数个

查看试题解析
6. 通过大量重复抛掷两枚均匀硬币的试验，出现两个反面的成功率大约稳定在 $($ $)$

A、 $25 %$ B、 $50 %$ C、 $75 %$ D、 $100 %$

查看试题解析
7. 关于x的方程 $x^{2} + ax + b = 0$ 的两根为2与 $- 3$ ，则二次三项式 $x^{2} + ax + b$ 可分解为（）

A、 $(x - 2) (x + 3)$ B、 $(x + 2) (x - 3)$ C、 $2 (x - 2) (x + 3)$ D、 $2 (x + 2) (x - 3)$

查看试题解析
8. 关于反比例函数 $y = - \frac{1}{x}$ ，下列说法正确的是（）

A、图象过（1，1）点 B、图象在第一、三象限 C、当x>0时，y随x的增大而减小 D、当x<0时，y随x的增大而增大

查看试题解析
9. 已知：如图， $AB / / CD / / EF$ ，BD： $DF = 3$ ：5，那么下列结论正确的是（）

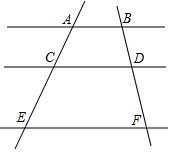A、 $\frac{AC}{AE} = \frac{3}{5}$ B、 $\frac{AB}{CD} = \frac{3}{5}$ C、 $\frac{CE}{AE} = \frac{5}{8}$ D、 $\frac{CD}{EF} = \frac{3}{5}$

查看试题解析

二、填空题

10. 若关于x的一元二次方程 $2 x^{2} + (2 k + 1) x - (4 k - 1) = 0$ 的二次项系数、一次项系数、常数项的和是0，则 $k =$ .

查看试题解析
11. 同时抛掷两个质地均匀的正方形骰子，骰子的六个面上分别刻有1到6的点数，则两个骰子向上的一面的点数和为6的概率为.

查看试题解析
12. 已知 $△ ABC$ ∽ $△ DEF$ ，AB： $DE = 4$ ：5，那么 $S_{△ ABC}$ ： $S_{△ DEF} =$ .

查看试题解析
13. 已知函数 $y = (m - 2) x^{| m | - 3}$ 是反比例函数，则 $m =$ .

查看试题解析
14. 已知，反比例函数 $y = \frac{6}{x}$ 在第一象限的图象如图所示，点A在图象上， $AB ⊥ OB$ ，则 $△ OAB$ 的面积是.

查看试题解析
15. 如图，六边形ABCDEF与六边形 $A'B'C'D'E'F'$ 是位似图形，O为位似中心， $OA'$ ： $OA = 1$ ：2，则B′C′： $BC =$ .

查看试题解析
16. 如图，正方形ABCD的边长为4，H在CD的延长线上，四边形CEFH也为正方形，则 $△ D B F$ 的面积为.

查看试题解析
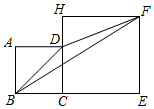17. 在 $△ A B C$ 中， $B C = a .$ 作BC边的三等分点 $C_{1}$ ，使得 $C C_{1}$ ： $B C_{1} = 1$ ：2，过点 $C_{1}$ 作AC的平行线交AB于点 $A_{1}$ ，过点 $A_{1}$ 作BC的平行线交AC于点 $D_{1}$ ，作 $B C_{1}$ 边的三等分点 $C_{2}$ ，使得 $C_{1} C_{2}$ ： $B C_{2} = 1$ ：2，过点 $C_{2}$ 作AC的平行线交AB于点 $A_{2}$ ，过点 $A_{2}$ 作BC的平行线交 $A_{1} C_{1}$ 于点 $D_{2}$ ；如此进行下去，则线段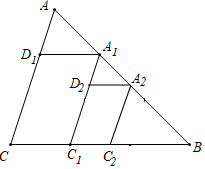 $A_{n} D_{n}$ 的长度为.

查看试题解析

三、解答题

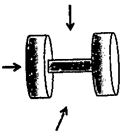
18. 用适当的方法解下列一元二次方程

(1)、 $3 x^{2} - 10 x + 3 = 0$ ；

(2)、 $(2 x - 3) (x + 1) = (2 - x) (x + 1)$

查看试题解析
19. 画出如图所示几何体的主视图、左视图和俯视图.

查看试题解析
20. 已知：如图，在正方形ABCD中，Q是CD的中点， $PQ ⊥ AQ .$ 求证： $BP = 3 CP$ .

查看试题解析
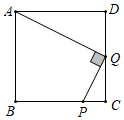21. 如图，路灯 $($ 点 $P)$ 距地面6m，身高 $1.5 m$ 的学生小明从路灯的底部点O处，沿射线OH走到距路灯底部9m的点B处，此时小明的身影为BN，接着小明走到点N处，此时的身影为 $A M .$ 求学生小明的身影长度变长了多少米 $. ($ 小明如图中BD、AC所示 $)$

查看试题解析
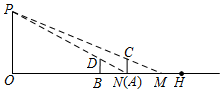22. 一个盒子中有1个红球，1个白球和2个蓝球，这些球除颜色外都相同，从中随机摸出1个球，记下颜色后放回，再从中随机摸出1个球.

(1)、两次摸到相同颜色的球的概率；

(2)、在上面的问题中，如果从中随机摸出1个球，记下颜色后不放回，再从中随机摸出1个球，求两次摸到的球的颜色能配成紫色 $($ 红色与蓝色配成紫色 $)$ 的概率.

查看试题解析
23. 已知，一次函数 $y = mx + n$ 交反比例函数 $y = \frac{k}{x}$ 于点A和B，交x轴于点C，且点A的坐标是 $(1 ， 2)$ ， $AC = 2 BC$ ，过点A向x轴作垂线，垂足为点D.

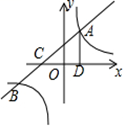(1)、求反比例函数的解析式；

(2)、求 $△ ACD$ 的面积.

查看试题解析
24. 已知：如图，在平行四边形ABCD中，M、N分别是AD和BC的中点.

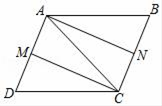(1)、求证：四边形AMCN是平行四边形；

(2)、若AC＝CD，求证四边形AMCN是矩形；

(3)、若∠ACD＝90°，求证四边形AMCN是菱形；

(4)、若AC＝CD，∠ACD＝90°，求证四边形AMCN是正方形.

查看试题解析
25. 如图，在 $△ ABC$ 中， $∠ B = 90^{\circ}$ ， $AB = 12 cm$ ， $BC = 16 cm$ ，点Q从点B开始沿BC边向点C移动，点Q的速度为 $2 cm / s .$ 点P从点B开始沿BA边向点A移动，然后再返回B点，点P的速度为 $3 cm / s$ .

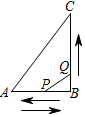(1)、如果P、Q分别从点B同时出发，那么几秒后 $△ PBQ$ 的面积等于 $21 {cm}^{2}$ ？

(2)、如果P、Q分别从点B同时出发， $△ PBQ$ 的面积能否等于 $51 {cm}^{2}$ ？说明理由.

查看试题解析