辽宁锦州市2019届九年级上学期数学期末考试试卷

试卷更新日期：2020-01-15 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 如图，一个空心圆柱体，其左视图正确的是（   ）

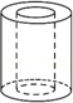    A、 B、 C、 D、

    查看试题解析

  • 2. 关于x的一元二次方程x2+x+1＝0的根的情况是（  ）
    A、两个不等的实数根 B、两个相等的实数根 C、没有实数根 D、无法确定

    查看试题解析

  • 3. 有3张纸牌，分别是红桃2，红桃3，黑桃A，把纸牌洗匀后甲先抽取一张，记下花色和数字后将牌放回，洗匀后乙再抽取一张，则两人抽的纸牌均为红桃的概率是（   ）
    A、49 B、59 C、13 D、23

    查看试题解析

  • 4. 下列说法正确的是（   ）
    A、有两个角为直角的四边形是矩形 B、矩形的对角线相等 C、平行四边形的对角线相等 D、对角线互相垂直的四边形是菱形

    查看试题解析

  • 5. 如图，△ABC中，点D，E分别在边AB，BC上，DE∥AC，若DB＝4，AB＝6，BE＝3，则EC的长是（   ）

    A、4 B、2 C、32 D、52

    查看试题解析

  • 6. 已知反比例函数 y=−1x ，下列结论不正确的是（     ）.
    A、该函数图象经过点（-1，1） B、该函数图象在第二、四象限 C、当x<0时，y随x增大而减小 D、当x>1时， -1<y<0

    查看试题解析

  • 7. 如图，在矩形ABCD中，AB=8厘米，BC=10厘米，点E在边AB上，且AE=2厘米，如果动点P在线段BC上以2厘米/秒的速度由B点向C点运动，同时，动点Q在线段CD上由C点向D点运动，设运动时间为t秒，当△BPE与△CQP全等时，t的值为（ ）

    A、2 B、1.5或2 C、2.5 D、2或2.5

    查看试题解析

  • 8. 如图，已知∠MON＝30°，B为OM上一点，BA⊥ON于点A，四边形ABCD为正方形，P为射线BM上一动点，连结CP，将CP绕点C顺时针方向旋转90°得CE，连接BE，若AB＝2，则BE的最小值为（  ）

    A、3 +1 B、2 3 ﹣1 C、3 D、4﹣ 3

    查看试题解析

二、填空题

  • 9. 方程x2＝2x的解是.

    查看试题解析

  • 10. 某地区为估计该地区黄羊的只数，先捕捉20只黄羊给它们分别作上标志，然后放回，待有标志的黄羊完全混合于黄羊群后，第二次捕捉60只黄羊，发现其中2只有标志.从而估计该地区有黄羊只.

    查看试题解析

  • 11. 小明的身高为1.6米，他在阳光下的影长为0.8米，同一时刻，测得校园的旗杆的影长为4.5米，则该旗杆的高为米.

    查看试题解析

  • 12. 如图，已知点A在反比例函数图象上，AC⊥y轴于点C，点B在x轴的负半轴上，且△ABC的面积为3，则该反比例函数的表达式为.

    查看试题解析

  • 13. 如图，某小区有一块长为30m，宽为24m的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为480m2 ， 两块绿地之间及周边有宽度相等的人行通道，设人行通道的宽度为xm，则可列方程为.

    查看试题解析

  • 14. 如图，在菱形ABCD中，∠BAD＝120°，CE⊥AD，且CE＝BC，连接BE交对角线AC于点F，则∠EFC＝°

    查看试题解析

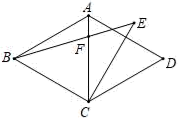  • 15. 如图，在平面直角坐标系中，O为坐标原点，点A，B的坐标分别为（0，4），（﹣3，0），E为AB的中点，EF∥AO交OB于点F，AF与EO交于点P，则EP的长为.

    查看试题解析

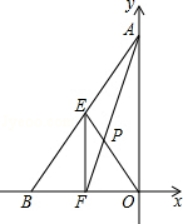  • 16. 如图，正方形A1ABC的边长为1，正方形A2A1B1C1边长为2.正方形A3A2B2C2边长为4，…依此规律继续做正方形An+1AnBn∁n ， 其中点A，A1 ， A2 ， A3 ， …在同一条直线上，连接AC1交A1B1于点D1 ， 连接A1C2交A2B2于点D2 ， …，若记△AA1D1的面积为S1 ， △A1A2D2的面积为S2…，△An﹣1AnDn的面积为Sn ， 则S2019＝.

    查看试题解析

三、解答题

  • 17. 用适当的方法解下列一元二次方程：
    (1)、（x﹣1）2＝2；
    (2)、2x2+5x＝﹣2

    查看试题解析

  • 18. 如图，在平面直角坐标系中，△ABC的顶点都在小方格的格点上.

    (1)、点A的坐标是；点C的坐标是；
    (2)、以原点O为位似中心，将△ABC缩小，使变换后得到的△A1B1C1与△ABC对应边的比为1：2，请在网格中画出△A1B1C1；
    (3)、△A1B1C1的面积为.

    查看试题解析

  • 19. 某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压P（单位：千帕）随气体体积V（单位：立方米）的变化而变化，P随V的变化情况如下表所示.

    P

    1.5

    2

    2.5

    3

    4

    …

    V

    64

    48

    38.4

    32

    24

    …
    (1)、写出符合表格数据的P关于V的函数表达式；
    (2)、当气球的体积为20立方米时，气球内气体的气压P为多少千帕？
    (3)、当气球内的气压大于144千帕时，气球将爆炸，依照（1）中的函数表达式，基于安全考虑，气球的体积至少为多少立方米？

    查看试题解析

  • 20. 小明和小亮两同学做游戏，游戏规则是：有一个不透明的盒子，里面装有两张红卡片，两张绿卡片，卡片除颜色外其他均相同，两人先后从盒子中取出一张卡片（不放回），若两人所取卡片的颜色相同，则小明获胜，否则小亮获胜.
    (1)、请用画树状图或列表法列出游戏所有可能的结果；
    (2)、请根据你的计算结果说明游戏是否公平，若不公平，你认为对谁有利？

    查看试题解析

  • 21. 如图，在△ABC中，D、E分别是边AC、BC的中点，F是BC延长线上一点，∠F＝∠B.

    (1)、若AB＝10，求FD的长；
    (2)、若AC＝BC，求证：△CDE∽△DFE.

    查看试题解析

  • 22. 利民商场经营某种品牌的T恤，购进时的单价是300元，根据市场调查：在一段时间内，销售单价是400元时，销售量是60件，销售单价每涨10元，销售量就减少1件.设这种T恤的销售单价为x元（x＞400）时，销售量为y件、销售利润为W元.
    (1)、请分别用含x的代数式表示y和W（把结果填入下表）：

    销售单价（元）

    x

    销售量y（件）

    销售利润W（元）

    (2)、该商场计划实现销售利润10000元，并尽可能增加销售量，那么x的值应当是多少？

    查看试题解析

  • 23. 如图，一次函数y＝mx+n（m≠0）的图象与反比例函数y＝ kx （k≠0）的图象交于第一、三象限内的A，B两点，与y轴交于点C，过点B作BM⊥x轴，垂足为点M，BM＝OM＝2，点A的纵坐标为4.

    (1)、求该反比例函数和一次函数的表达式；
    (2)、直线AB交x轴于点D，过点D作直线l⊥x轴，如果直线l上存在点P，坐标平面内存在点Q.使O、P、A、Q四点构成的四边形是矩形，求出点P的坐标.

    查看试题解析

  • 24. 如图1，在正方形ABCD中，E是边BC上的点，将线段DE绕点E逆时针旋转90°得到EF，过点C作CG∥EF交BA（或其延长线）于点G，连接DF，FG.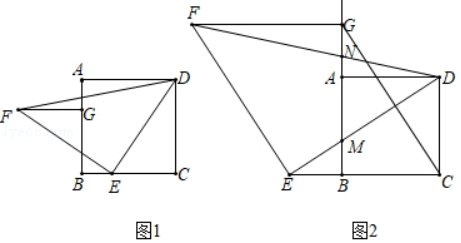

    (1)、FG与CE的数量关系是 ， 位置关系是.
    (2)、如图2，若点E是CB延长线上的点，其它条件不变.

    ①（1）中的结论是否仍然成立？请作出判断，并给予证明；

    ②DE，DF分别交BG于点M，N，若BC＝2BE，求 MNBC .

    查看试题解析