江苏省镇江市2019届九年级上学期数学期末考试试卷
试卷更新日期:2020-01-15 类型:期末考试
一、单选题
-
1. 解一元二次方程x2﹣8x﹣5=0,用配方法可变形为( )A、(x+4)2=11 B、(x﹣4)2=11 C、(x+4)2=21 D、(x﹣4)2=212. 将抛物线 沿y轴翻折,所得抛物线的函数表达式是( )A、 B、 C、 D、3. 下列说法正确的是( )A、某种彩票的中奖机会是 则买100张这种彩票一定会中奖 B、为了解全国中学生的睡眠情况,应该采用普查的方式 C、一组数据3,4,5,5,5,6,10的平均数大于中位数 D、同时抛掷两枚均匀的硬币,出现一枚正面朝上且另一枚反面朝上的概率是4. 如图,A,D是⊙O上的两个点,BC是直径,若∠D=34°,则∠OAC等于( )
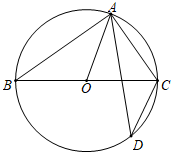 A、68° B、58° C、72° D、56°5. 已知二次函数 ,点 与点 都在该函数的图象上,且 是正整数,若满足 的点 有且只有3个,则 的取值范围是( )A、 B、 C、 D、
A、68° B、58° C、72° D、56°5. 已知二次函数 ,点 与点 都在该函数的图象上,且 是正整数,若满足 的点 有且只有3个,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
6. 已知关于x的方程 的一个根是0,则 .7. 若圆锥的母线长为4cm,其侧面积 ,则圆锥底面半径为cm.8. 某公司今年4月份营业额为100万元,6月份营业额达到121万元,该公司营业额的月均增长率为x,则可列方程为.9. 若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根,则m的值为 .10. 某单位要招聘1名英语翻译,张明参加招聘考试的成绩如表所示:
成绩
听
说
读
写
张明
95
90
90
90
若把听、说、读、写的成绩按4:3:2:1计算平均成绩,则张明的平均成绩为.
11. 如图,A,B,C是⊙O上的点,若∠BOC=100°,则∠BAC= ° 12. 若二次函数y=(m+1)x|m|+4x﹣16的图象开口向下,则m=.13. 已知二次函数 的顶点为 ,则其图象与y轴的交点坐标为.14. 小红随机地在如图所示的边长为6的正三角形及其内部区域投针,则针扎到其内切圆 阴影 区域的概率为.
12. 若二次函数y=(m+1)x|m|+4x﹣16的图象开口向下,则m=.13. 已知二次函数 的顶点为 ,则其图象与y轴的交点坐标为.14. 小红随机地在如图所示的边长为6的正三角形及其内部区域投针,则针扎到其内切圆 阴影 区域的概率为. 15. 已知二次函数 ,当 时,x的取值范围是.16. 如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为经过点(1,0)且垂直于x轴的直线.给出四个结论:①abc>0;②当x>1时,y随x的增大面减小;③4a﹣2b+c>0;④3a+c>0.其中正确的结论是(写出所有正确结论的序号)
15. 已知二次函数 ,当 时,x的取值范围是.16. 如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为经过点(1,0)且垂直于x轴的直线.给出四个结论:①abc>0;②当x>1时,y随x的增大面减小;③4a﹣2b+c>0;④3a+c>0.其中正确的结论是(写出所有正确结论的序号) 17. 在平面直角坐标系中,点A、B、C的坐标分别为 、 、 ,点E是 的外接圆上一点,BE交线段AC于点D,若 ,则点D的坐标为.
17. 在平面直角坐标系中,点A、B、C的坐标分别为 、 、 ,点E是 的外接圆上一点,BE交线段AC于点D,若 ,则点D的坐标为.
三、解答题
-
18. 解方程:(1)、x2﹣3x=0(2)、2x2﹣4x﹣5=0(3)、x(x﹣1)=0(4)、(x﹣1)2=3x﹣319. 某校为市体校选拔一名篮球队员 教练对王亮和李刚两名同学进行5次3分投篮测试,每人每次投10个球,下图记录的是这两名同学5次投篮中所投中的个数.
 (1)、请你根据图中的数据,填写下表
(1)、请你根据图中的数据,填写下表姓名
平均分
众数
极差
方差
王亮
7
7
李刚
7
5
(2)、你认为谁的成绩比较稳定,为什么?(3)、若你是教练,你打算选谁参赛?请利用以上数据或图中信息简要说明理由.20. 一只不透明的袋子中装有2个红球和1个白球这些球除颜色外都相同.(1)、小明认为,搅匀后从中任意摸出一个球,不是白球就是红球,因此摸出白球和红球是等可能的你同意吗?为什么.(2)、搅匀后从中一次摸出两个球,请通过列表或树状图求两个球是一红一白的概率;(3)、在这只袋中再放入若干个白球,搅匀后从中任意摸出一个球,要使摸出白球的概率为 ,应再放入多少个白球?21. 如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
①在图中作出△ABC的外接圆(保留必要的作图痕迹,不写作法),写出圆心坐标;
②若在x轴的正半轴上有一点D,且∠ADB=∠ACB,写出点D的坐标.
22. 二次函数 的图象与x轴交于 、B两点,与y轴交于点 ,其顶点为D.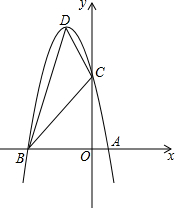 (1)、求这个二次函数的表达式;(2)、求 的面积.23. 已知京润生物制品厂生产某种产品的年产量不超过800吨,生产该产品每吨所需相关费为10万元,且生产出的产品都能在当年销售完.产品每吨售价y(万元)与年产量x(吨)之间的函数关系如图所示
(1)、求这个二次函数的表达式;(2)、求 的面积.23. 已知京润生物制品厂生产某种产品的年产量不超过800吨,生产该产品每吨所需相关费为10万元,且生产出的产品都能在当年销售完.产品每吨售价y(万元)与年产量x(吨)之间的函数关系如图所示 (1)、当该产品年产量为多少吨时,当年可获得7500万元毛利润?(毛利润=销售额﹣相关费用)(2)、当该产品年产量为多少吨时,该厂能获得当年销售的是大毛利润?最大毛利润多少万元.24. 如图,AB是⊙O的直径,点D是⊙O外一点,AB=AD,BD交⊙O于点C,AD交⊙O于点E,点P是AC的延长线上一点,连接PB、PD,且PD⊥AD
(1)、当该产品年产量为多少吨时,当年可获得7500万元毛利润?(毛利润=销售额﹣相关费用)(2)、当该产品年产量为多少吨时,该厂能获得当年销售的是大毛利润?最大毛利润多少万元.24. 如图,AB是⊙O的直径,点D是⊙O外一点,AB=AD,BD交⊙O于点C,AD交⊙O于点E,点P是AC的延长线上一点,连接PB、PD,且PD⊥AD (1)、判断PB与⊙O的位置关系,并说明理由;(2)、连接CE,若CE=3,AE=7,求⊙O的半径.25. 如图1,有一块直角三角板,其中 , , ,A、B在x轴上,点A的坐标为 ,圆M的半径为 ,圆心M的坐标为 ,圆M以每秒1个单位长度的速度沿x轴向右做平移运动,运动时间为t秒;
(1)、判断PB与⊙O的位置关系,并说明理由;(2)、连接CE,若CE=3,AE=7,求⊙O的半径.25. 如图1,有一块直角三角板,其中 , , ,A、B在x轴上,点A的坐标为 ,圆M的半径为 ,圆心M的坐标为 ,圆M以每秒1个单位长度的速度沿x轴向右做平移运动,运动时间为t秒; (1)、求点C的坐标;(2)、当点M在 的内部且 与直线BC相切时,求t的值;(3)、如图2,点E、F分别是BC、AC的中点,连接EM、FM,在运动过程中,是否存在某一时刻,使 ?若存在,直接写出t的值,若不存在,请说明理由.26. 已知抛物线 ,其中 ,直线l是它的对称轴,把该抛物线沿着x轴水平向左平移 个单位长度后,与x轴交于点A、B, 在B的左侧 ,如图1,P为平移后的抛物线上位于第一象限内的一点
(1)、求点C的坐标;(2)、当点M在 的内部且 与直线BC相切时,求t的值;(3)、如图2,点E、F分别是BC、AC的中点,连接EM、FM,在运动过程中,是否存在某一时刻,使 ?若存在,直接写出t的值,若不存在,请说明理由.26. 已知抛物线 ,其中 ,直线l是它的对称轴,把该抛物线沿着x轴水平向左平移 个单位长度后,与x轴交于点A、B, 在B的左侧 ,如图1,P为平移后的抛物线上位于第一象限内的一点 (1)、点A的坐标为;(2)、若点P的横坐标为 ,求出当m为何值时 的面积最大,并求出这个最大值;(3)、如图2,AP交l于点D,当D为AP的中点时,求证: .
(1)、点A的坐标为;(2)、若点P的横坐标为 ,求出当m为何值时 的面积最大,并求出这个最大值;(3)、如图2,AP交l于点D,当D为AP的中点时,求证: .