江苏省宜兴市2019届九年级上学期数学期末考试试卷
试卷更新日期:2020-01-15 类型:期末考试
一、单选题
-
1. 已知一元二次方程x2+kx-3=0有一个根为1,则k的值为( )A、−2 B、2 C、−4 D、42. 将抛物线 向上平移2个单位后,得到的函数表达式是( )A、 B、 C、 D、3. 已知圆锥的底面半径为2cm,母线长为4cm,则圆锥的侧面积是( )A、 B、 C、 D、4. 在 中,点 、 分别为边 、 的中点,则 与 的面积之比为( )A、 B、 C、 D、5. 已知A样本的数据如下:67,68,68,71,66,64,64,72,B样本的数据恰好是A样本数据每个都加6,则A、B两个样本的下列统计量对应相同的是( )A、平均数 B、方差 C、中位数 D、众数6. 以下命题: 相等的圆心角所对的弧相等; 长度相等的弧是等弧; 直径所对的圆周角是直角; 抛物线 的对称轴是直线 ,其中真命题的个数是( )A、0 B、1 C、2 D、37. 已知 的半径为3, ,点P是线段OA的中点,则点P与 的位置关系是( )A、点P在 内 B、点P在 上 C、点P在 外 D、以上都有可能8. 如图, ,直线 与 分别相交于点 和点 ,若 , ,则 的长是( )
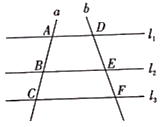 A、 B、 C、6 D、109. 如图,在矩形ABCD中,AB=16,AD>AB,以A为圆心裁出一扇形ABE(E在AD上),将扇形ABE围成一个圆锥(AB和AE重合),则此圆锥的底面圆半径是( )
A、 B、 C、6 D、109. 如图,在矩形ABCD中,AB=16,AD>AB,以A为圆心裁出一扇形ABE(E在AD上),将扇形ABE围成一个圆锥(AB和AE重合),则此圆锥的底面圆半径是( )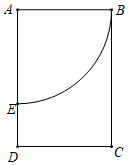 A、4 B、8 C、4 D、1610. 如图,在平面直角坐标系中, , , 半径为2,P为 上任意一点,E是PC的中点,则OE的最小值是( )
A、4 B、8 C、4 D、1610. 如图,在平面直角坐标系中, , , 半径为2,P为 上任意一点,E是PC的中点,则OE的最小值是( )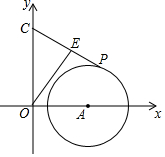 A、1 B、 C、2 D、
A、1 B、 C、2 D、二、填空题
-
11. 一元二次方程 的解是 .12. 如果 且 ,则 .13. 某厂一月份生产某机器100台,计划三月份生产160台.设二、三月份每月的平均增长率为x,根据题意列出的方程是 .14. 如图,AB是 的直径,弦 于点E, , ,则 cm.
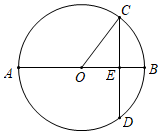 15. 如图,四边形ABCD内接于 ,AB是直径, ,过C点的切线CE与直线AB交于E点,则 的度数为.
15. 如图,四边形ABCD内接于 ,AB是直径, ,过C点的切线CE与直线AB交于E点,则 的度数为. 16. 如图,已知⊙O的半径是4,点A、B、C在⊙O上,若四边形OABC为菱形,则图中阴影部分面积为.
16. 如图,已知⊙O的半径是4,点A、B、C在⊙O上,若四边形OABC为菱形,则图中阴影部分面积为.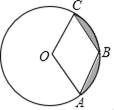 17. 如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则AG:GF的值是.
17. 如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则AG:GF的值是. 18. 抛物线 与x轴交于A、B两点,且A、B两点在 与原点之间 不包含端点 ,则a的取值范围是.
18. 抛物线 与x轴交于A、B两点,且A、B两点在 与原点之间 不包含端点 ,则a的取值范围是.三、解答题
-
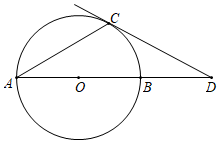
19. 如图,AB是 的直径,AC是 的弦过点C的切线交AB的延长线于点D,若 ,试求 的度数.
 20. 解方程(1)、 ;(2)、 .21. 已知关于x的一元二次方程 有两个不相等的实数根,求m的取值范围.22. 一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为 .(1)、求口袋中黄球的个数;(2)、甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;23. 如图,正方形ABCD中,M为BC上一点, ,MN交CD于点N.
20. 解方程(1)、 ;(2)、 .21. 已知关于x的一元二次方程 有两个不相等的实数根,求m的取值范围.22. 一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为 .(1)、求口袋中黄球的个数;(2)、甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,求两次摸出都是红球的概率;23. 如图,正方形ABCD中,M为BC上一点, ,MN交CD于点N.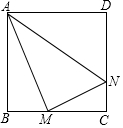 (1)、求证: ∽ ;(2)、若 , ,求DN的长.24. 如图,在 的网格中,有一格点三角形 说明:顶点都在网格线交点处的三角形叫做格点三角形
(1)、求证: ∽ ;(2)、若 , ,求DN的长.24. 如图,在 的网格中,有一格点三角形 说明:顶点都在网格线交点处的三角形叫做格点三角形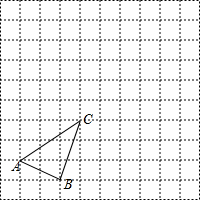 (1)、①将 先向右平移5个单位,再向上平移2个单位,得到 ,请直接画出平移后的 ;
(1)、①将 先向右平移5个单位,再向上平移2个单位,得到 ,请直接画出平移后的 ;②将 绕点C顺时针旋转 ,得到 ,请直接画出旋转后的 友情提醒:别忘了标上相应的字母
(2)、在第(1)②小题的旋转过程中,点 所经过的路线长 结果保留 .25. 在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.销售量y(千克)
…
34.8
32
29.6
28
…
售价x(元/千克)
…
22.6
24
25.2
26
…
(1)、某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)、如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
26. 已知 ,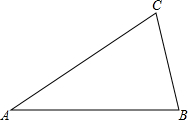 (1)、用无刻度的直尺和圆规作 ,使 且 的面积为 面积的一半,只需要画出一个 即可 作图不必写作法,但要保留作图痕迹(2)、在 中,若 , ,则 面积的最大值是27. 如图,在平面直角坐标系中,点A、B的坐标分别为 , ,点M是AO中点, 的半径为2.
(1)、用无刻度的直尺和圆规作 ,使 且 的面积为 面积的一半,只需要画出一个 即可 作图不必写作法,但要保留作图痕迹(2)、在 中,若 , ,则 面积的最大值是27. 如图,在平面直角坐标系中,点A、B的坐标分别为 , ,点M是AO中点, 的半径为2.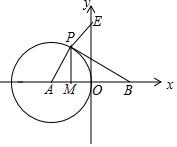 (1)、若 是直角三角形,则点P的坐标为 直接写出结果(2)、若 ,则BP与 有怎样的位置关系?为什么?(3)、若点E的坐标为 ,那么 上是否存在一点P,使 最小,如果存在,求出这个最小值,如果不存在,简要说明理由.28. 如图,二次函数 的图象交x轴于A、B两点 其中点A在点B的左侧 ,交y轴正半轴于点C,且 ,点D在该函数的第一象限内的图象上.
(1)、若 是直角三角形,则点P的坐标为 直接写出结果(2)、若 ,则BP与 有怎样的位置关系?为什么?(3)、若点E的坐标为 ,那么 上是否存在一点P,使 最小,如果存在,求出这个最小值,如果不存在,简要说明理由.28. 如图,二次函数 的图象交x轴于A、B两点 其中点A在点B的左侧 ,交y轴正半轴于点C,且 ,点D在该函数的第一象限内的图象上.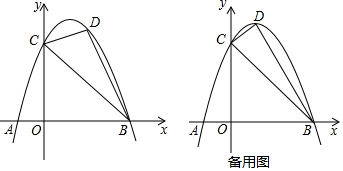 (1)、求点A、点B的坐标;(2)、若 的最大面积为 平方单位,求点D的坐标及二次函数的关系式;(3)、若点D为该函数图象的顶点,且 是直角三角形,求此二次函数的关系式.
(1)、求点A、点B的坐标;(2)、若 的最大面积为 平方单位,求点D的坐标及二次函数的关系式;(3)、若点D为该函数图象的顶点,且 是直角三角形,求此二次函数的关系式.