江苏省扬州市高邮市2019届九年级上学期数学期末考试试卷
试卷更新日期：2020-01-15 类型：期末考试
一、单选题
-
1. 一组数据：1，5，﹣2，0，﹣1的极差是（ ）A、5 B、6 C、7 D、82. 用配方法解方程x2﹣6x+7＝0，将其化为(x+a)2＝b的形式，正确的是（ ）A、(x+3)2＝2 B、(x﹣3)2＝16 C、(x﹣6)2＝2 D、(x﹣3)2＝23. 若⊙O的直径为12，点P在⊙O外，则OP的长可能是（ ）A、4 B、5 C、6 D、74. 若将二次函数y＝x2﹣1的图象向上平移2个单位长度，再向右平移3个单位长度，则平移后的二次函数的顶点坐标为（ ）A、(﹣3，1) B、(3，1) C、(2，2) D、(﹣3，﹣3)5. Rt△ABC中，∠C＝90°，∠A、∠C所对的边分别为a、c，下列式子中，正确的是（ ）A、a＝c•cotA B、a＝c•tanA C、a＝c•cosA D、a＝c•sinA6. 如图，AB为半圆O的直径，现将一块等腰直角三角板如图放置，锐角顶点P在半圆上，斜边过点B，一条直角边交该半圆于点Q.若AB＝2，则线段BQ的长为（ ）
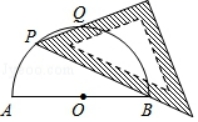A、 B、 C、 D、17. 如图，在平行四边形ABCD中，点E在边DC上，DE：EC=4：1，连接AE、BE，AE交BD于点F，则△BEC的面积与△BEF的面积之比为（ ）
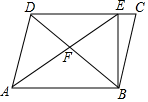A、1：2 B、9：16 C、3：4 D、9：208. 若x1 ， x2(x1＜x2)是方程(x﹣m)(x﹣3)＝﹣1(m＜3)的两根，则实数x1 ， x2 ， 3，m的大小关系是（ ）A、m＜x1＜x2＜3 B、x1＜m＜x2＜3 C、x1＜m＜3＜x2 D、x1＜x2＜m＜3二、填空题
-
9. 一个不透明的口袋中有6个完全相同的小球，把它们分别标号为1，2，3，4，5，6，从中随机摸取一个小球，取出的小球标号恰好是偶数的概率是 ．10. 某一时刻，长为1m的标杆影长为0.8m，此时身高为1.75m的小明影长为m.11. 在比例尺为1：2000000的地图上，港珠澳大桥的主桥图上距离为1.48cm，则港珠澳大桥的主桥长度为km.12. 我市某楼盘计划以每平方9200元的均价销售，为加快资金周转，房地产开发商对价格经过连续两次下调后，决定以每平方7452元的均价开盘销售，则平均每次下调的百分率是.13. 若一个圆锥的主视图如图，其中AB＝6cm，BC＝4cm，则该圆锥的侧面积为cm2
14. 已知m为一元二次方程x2﹣3x+5＝0的一根，则代数式2m2﹣6m+2029的值为 .15. 如图，将Rt△ACD与Rt△CAB直角边AC重合，∠DAC＝∠ACB＝90°，若AC＝AD，∠B＝30°，则△AED与△CEB的面积比为.
16. 若二次函数y＝(k+1)x2﹣2 x+k的最高点在x轴上，则k＝.17. 如图，由四个全等的直角三角形围成的大正方形ABCD的面积为34，小正方形EFGH的面积为4，则tan∠DCG的值为.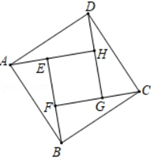
18. 如图，△ABC中，∠ACB＝90°，BC＝3，cos∠B＝ ，将△ABC绕点C顺时针旋转90°得到△AB'C，P为线段AB上的动点，以点P为圆心，PA长为半径作⊙P，当⊙P与△A′B′C的一边所在的直线相切时，⊙P的半径为.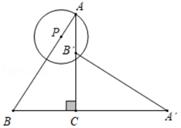
三、解答题
-
19.(1)、计算：2sin30°+( )﹣1+(4﹣π)0+ .(2)、解方程：x2+2x﹣3＝0.20. “绿色飞检”中对一所初中的九年级学生在试卷讲评课上参与学习的深度与广度进行调查，调查项目分为主动质疑、独立思考、专注听讲、讲解题目四项.调查组随机抽取了若干名九年级学生的参与情况，绘制了如下两幅不完整的统计图，请根据图中所给信息解答下列问题：
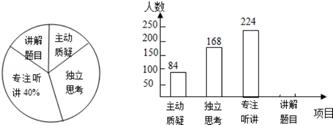(1)、在这次评价中，一共抽查了名学生；(2)、请将条形图补充完整；(3)、如果全市有5200名九年级学生，那么在试卷评讲课中，“独立思考”的九年级学生有多少人21. 为积极配合我市文明城市创建，居委会组织了两个检查组，分别对辖区内新华园、清华园、德才园、御花园四个小区“垃圾分类”和“违规停车”的情况进行抽查，每个检查组随机抽取辖区内的一个小区进行检查.(1)、“违规停车”检查组抽到新华园小区的概率为 ；(2)、求两个组恰好同时抽到御花园小区进行检查的概率.22. 关于x的一元二次方程x2﹣2x﹣(n﹣1)＝0有两个不相等的实数根.(1)、求n的取值范围；(2)、若n为取值范围内的最小整数，求此方程的根.23. 如图，△ABC中，D是BC上一点，∠DAC＝∠B，E为AB上一点.
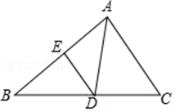(1)、求证：△CAD∽△CBA；(2)、若DE∥AC，BD＝10，DC＝8，求DE的长.24. 如图，小华在体育馆的看台P处进行观测，测得另一看台观众A处的俯角为15°，观众B处的俯角为60°，已知观众A、B所在看台的坡度i(即tan∠ABC)为1： ，点P、H、B、C、A在同一个平面上，点H、B、C在同一条直线上，且PH⊥HC，PH＝15米.
(1)、AB所在看台坡角∠ABC＝度；(2)、求A、B两点间的距离.(结果精确到0.1米，参考数据： ≈1.73)25. 如图，已知⊙O是△ABC的外接圆，连接OC，过点A作AD∥OC，交BC的延长线于D，AB交OC于E，∠ABC＝45°．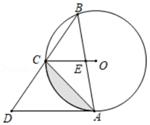
(1)、求证：AD是⊙O的切线；(2)、若AE＝ ，CE＝3．①求⊙O的半径；
②求图中阴影部分的面积．
26. “春节”前夕，某超市购进某种品牌礼品，每盒进价是40元，超市规定每盒售价不得少于45元，设每盒售价为x(元)，每天的销售量y(盒)，y与x成一次的函数关系，经过市场调查获得部分数据如下表：每盒售价为x(元)
45
50
55
…
每天的销售量y(盒)
450
400
350
…
(1)、试求出y与x之间的函数关系式；(2)、当每盒售价定为多少元时，每天销售的利润P(元)最大？最大利润是多少？(3)、物价部门规定：这种礼品每盒售价不得高于60元，如果超市想要每天获得不低于5250元的利润，那么超市每天至少销售这种礼品多少盒？27. 如图1，抛物线y＝ax2+bx+c(a≠0)与x轴交于A，B两点，点P在抛物线上(与A，B两点不重合)，若△ABP的三边满足AP2+BP2＝AB2 ， 则我们称点P为抛物线y＝ax2+bx+c(a≠0)的勾股点.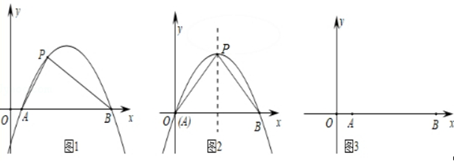
(1)、直接写出抛物线y＝x2﹣1的勾股点坐标为 ；(2)、如图2，已知抛物线：y＝ax2+bx(a＜0，b＞0)与x轴交于A、B两点，点P为抛物线的顶点，问点P能否为抛物线的勾股点，若能，求出b的值；(3)、如图3，在平面直角坐标系中，点A(2，0)，B(12，0)，点P到x轴的距离为1，点P是过A、B两点的抛物线上的勾股点，求过P、A、B三点的抛物线的解析式和点P的坐标.28. 已知，如图Rt△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，点P为AC的中点，Q从点A运动到B，点Q运动到点B停止，连接PQ，取PQ的中点O，连接OC，OB.
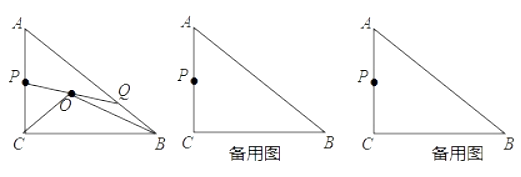(1)、若△ABC∽△APQ，求BQ的长；(2)、在整个运动过程中，点O的运动路径长；(3)、以O为圆心，OQ长为半径作⊙O，当⊙O与AB相切时，求△COB的面积.