河南省许昌市2019届九年级数学中考一模试卷
试卷更新日期:2020-01-15 类型:中考模拟
一、单选题
-
1. 下列四个数中,是正整数的是( )A、﹣1 B、0 C、 D、12. 据《经济日报》2018年5月21日报道:目前,世界集成电路生产技术水平最高已达到7nm(1nm=10﹣9m),主流生产线的技术水平为14~28nm,中国大陆集成电路生产技术水平最高为28nm.将28nm用科学记数法可表示为( )
A、28×10﹣9m B、2.8×10﹣8m C、28×109m D、2.8×108m3. 如图是由5个完全相同的小正方体搭建的几何体,若将最右边的小正方体拿走,则下列结论正确的是( ) A、主视图不变 B、左视图不变 C、俯视图不变 D、三视图都不变4. 下列运算中正确的是( )A、 B、 C、 D、5. 某校七年级2班近期准备组织一次朗诵活动,语文老师调查了全班学生平均每天的阅读时间,统计结果如下表所示,则在本次调查中,全班学生平均每天阅读时间的中位数和众数分别是( )
A、主视图不变 B、左视图不变 C、俯视图不变 D、三视图都不变4. 下列运算中正确的是( )A、 B、 C、 D、5. 某校七年级2班近期准备组织一次朗诵活动,语文老师调查了全班学生平均每天的阅读时间,统计结果如下表所示,则在本次调查中,全班学生平均每天阅读时间的中位数和众数分别是( ) A、2,1 B、1,1.5 C、1,2 D、1,16. 若二次函数 的图像与 轴有两个交点,则实数 的取值范围是( )A、 B、 C、 D、7. 如图,在 中, ,点 在 上, ,若 ,则 的度数为( )
A、2,1 B、1,1.5 C、1,2 D、1,16. 若二次函数 的图像与 轴有两个交点,则实数 的取值范围是( )A、 B、 C、 D、7. 如图,在 中, ,点 在 上, ,若 ,则 的度数为( )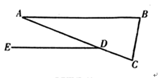 A、 B、 C、 D、8. 在一个不透明的袋子里装有两个黄球和一个白球,它们除颜色外都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球.两次都摸到黄球的概率是( )A、 B、 C、 D、9. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AC的中点,连接BD,按以下步骤作图:①分别以B,D为圆心,大于 BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )
A、 B、 C、 D、8. 在一个不透明的袋子里装有两个黄球和一个白球,它们除颜色外都相同,随机从中摸出一个球,记下颜色后放回袋子中,充分摇匀后,再随机摸出一个球.两次都摸到黄球的概率是( )A、 B、 C、 D、9. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AC的中点,连接BD,按以下步骤作图:①分别以B,D为圆心,大于 BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=( )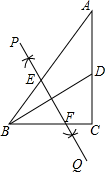 A、 B、1 C、 D、10. 如图1,在 中, ,点 从点 出发,沿 的路径匀速运动到点B停止,作 于点D,设点 运动的路程为x,PD长为y,y与x之间的函数关系图象如图2所示,当 时,y的值是( )
A、 B、1 C、 D、10. 如图1,在 中, ,点 从点 出发,沿 的路径匀速运动到点B停止,作 于点D,设点 运动的路程为x,PD长为y,y与x之间的函数关系图象如图2所示,当 时,y的值是( )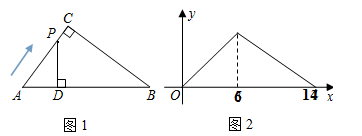 A、6 B、 C、 D、2
A、6 B、 C、 D、2二、填空题
-
11. 计算: 。12. 不等式组 的解集是。13. 已知点P(-2,m)和点Q(2,n)是一次函数y=2x+3的图象上的两点,则m与n的大小关系是.14. 如图,等边三角形 的边长为4,以 为直径的半圆 交 于点 ,交 于点 ,阴影部分的面积是。
 15. 如图,正方形ABCD的边长是2,点E是CD边的中点,点F是边BC上不与点B,C重合的一个动点,把∠C沿直线EF折叠,使点C落在点C′处.当△ADC′为等腰三角形时,FC的长为.
15. 如图,正方形ABCD的边长是2,点E是CD边的中点,点F是边BC上不与点B,C重合的一个动点,把∠C沿直线EF折叠,使点C落在点C′处.当△ADC′为等腰三角形时,FC的长为.
三、解答题
-
16. 先化简,再求值( ﹣ )÷ ,其中a,b满足a+b﹣ =0.17. 在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别
家庭藏书m本
学生人数
A
0≤m≤25
20
B
26≤m≤100
a
C
101≤m≤200
50
D
m≥201
66
根据以上信息,解答下列问题:
(1)、该调查的样本容量为 , a=;(2)、在扇形统计图中,“A”对应扇形的圆心角为°;(3)、若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.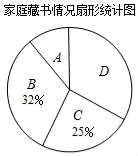 18. 如图,平行四边形ABCD放置在平面直角坐标系xOy中,已知A(-2,0),B(2,0),D(0,3),反比例函数y= (x>0)的图象经过点C.
18. 如图,平行四边形ABCD放置在平面直角坐标系xOy中,已知A(-2,0),B(2,0),D(0,3),反比例函数y= (x>0)的图象经过点C. (1)、求此反比例函数的解析式;(2)、问将平行四边形ABCD向上平移多少个单位,能使点B落在双曲线上?19. 如图, 是 ABC的外接圆,AB为直径,∠BAC的平分线交 于点D,过点D作DE AC分别交AC、AB的延长线于点E、F.
(1)、求此反比例函数的解析式;(2)、问将平行四边形ABCD向上平移多少个单位,能使点B落在双曲线上?19. 如图, 是 ABC的外接圆,AB为直径,∠BAC的平分线交 于点D,过点D作DE AC分别交AC、AB的延长线于点E、F. (1)、求证:EF是 的切线;(2)、若AC=4,CE=2,求 的长度.(结果保留 )20. 如图,某数学兴趣小组为测量一棵古树 和教学楼 的高,先在 处用高1.5米的测角仪测得古树顶端 的仰角 为 ,此时教学楼顶端 恰好在视线 上,再向前走9米到达 处,又测得教学楼顶端 的仰角 为 ,点 、 、 三点在同一水平线上.
(1)、求证:EF是 的切线;(2)、若AC=4,CE=2,求 的长度.(结果保留 )20. 如图,某数学兴趣小组为测量一棵古树 和教学楼 的高,先在 处用高1.5米的测角仪测得古树顶端 的仰角 为 ,此时教学楼顶端 恰好在视线 上,再向前走9米到达 处,又测得教学楼顶端 的仰角 为 ,点 、 、 三点在同一水平线上. (1)、计算古树 的高;(2)、计算教学楼 的高.(结果精确到0.1米,参考数据: , , , ).21. 某公司投入研发费用80万元(80万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为6元/件.此产品年销售量y(万件)与售价x(元/件)之间满足函数关系式y=﹣x+26.
(1)、计算古树 的高;(2)、计算教学楼 的高.(结果精确到0.1米,参考数据: , , , ).21. 某公司投入研发费用80万元(80万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为6元/件.此产品年销售量y(万件)与售价x(元/件)之间满足函数关系式y=﹣x+26.
(1)、求这种产品第一年的利润W1(万元)与售价x(元/件)满足的函数关系式;
(2)、该产品第一年的利润为20万元,那么该产品第一年的售价是多少?(3)、第二年,该公司将第一年的利润20万元(20万元只计入第二年成本)再次投入研发,使产品的生产成本降为5元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过12万件.请计算该公司第二年的利润W2至少为多少万元.
22.(1)、阅读理解利用旋转变换解决数学问题是一种常用的方法.如图1,点 是等边三角形 内一点, , , .求 的度数.
为利用已知条件,不妨把 绕点 顺时针旋转 得 ,连接 ,则 的长为;在 中,易证 ,且 的度数为 , 综上可得 的度数为;
 (2)、类比迁移
(2)、类比迁移如图2,点 是等腰 内的一点, , , , .求 的度数;
 (3)、拓展应用
(3)、拓展应用如图,在四边形 中, , , , ,请直接写出 的长.
 23. 如图,抛物线y=ax2+bx+3交y轴于点A,交x轴于点B(-3,0)和点C(1,0),顶点为点M.
23. 如图,抛物线y=ax2+bx+3交y轴于点A,交x轴于点B(-3,0)和点C(1,0),顶点为点M. (1)、求抛物线的解析式;(2)、如图,点E为x轴上一动点,若△AME的周长最小,请求出点E的坐标;(3)、点F为直线AB上一个动点,点P为抛物线上一个动点,若△BFP为等腰直角三角形,请直接写出点P的坐标.
(1)、求抛物线的解析式;(2)、如图,点E为x轴上一动点,若△AME的周长最小,请求出点E的坐标;(3)、点F为直线AB上一个动点,点P为抛物线上一个动点,若△BFP为等腰直角三角形,请直接写出点P的坐标.