河南省信阳市2019届数学中考一模试卷
试卷更新日期:2020-01-15 类型:中考模拟
一、单选题
-
1. 比较﹣1 , ,﹣1 , 的大小,结果正确的是( )A、﹣1 <﹣1 < < B、﹣1 <﹣1 < < C、﹣1 <﹣1 < < D、﹣1 <﹣1 < <2. 共享单车的投放使用为人们的工作和生活带来了极大的便利,不仅有效缓解了出行“最后一公里”问题,而且经济环保,据相关部门2018年11月统计数据显示,郑州市互联网租赁自行车累计投放超过49万辆,将49万用科学记数法表示正确的是( )A、4.9×104 B、4.9×105 C、0.49×104 D、49×1043. 如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列各运算中,计算正确的是( )A、a12÷a3=a4 B、(3a2)3=9a6 C、(a﹣b)2=a2﹣ab+b2 D、2a•3a=6a25. 郑州某中学在备考2018河南中考体育的过程中抽取该校九年级20名男生进行立定跳远测试,以便知道下一阶段的体育训练,成绩如下所示:
4. 下列各运算中,计算正确的是( )A、a12÷a3=a4 B、(3a2)3=9a6 C、(a﹣b)2=a2﹣ab+b2 D、2a•3a=6a25. 郑州某中学在备考2018河南中考体育的过程中抽取该校九年级20名男生进行立定跳远测试,以便知道下一阶段的体育训练,成绩如下所示:成绩(单位:米)
2.10
2.20
2.25
2.30
2.35
2.40
2.45
2.50
人数
2
3
2
4
5
2
1
1
则下列叙述正确的是( )
A、这些运动员成绩的众数是5 B、这些运动员成绩的中位数是2.30 C、这些运动员的平均成绩是2.25 D、这些运动员成绩的方差是0.07256. 如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )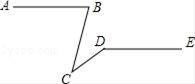 A、20° B、30° C、40° D、70°7. 如图,AB是⊙O的直径,点C,D在⊙O上,且点C,D在AB的异侧,连接AD,BD,OD,OC,若∠ABD=15°,且AD∥OC,则∠BOC的度数为( )
A、20° B、30° C、40° D、70°7. 如图,AB是⊙O的直径,点C,D在⊙O上,且点C,D在AB的异侧,连接AD,BD,OD,OC,若∠ABD=15°,且AD∥OC,则∠BOC的度数为( )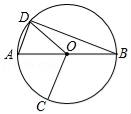 A、120° B、105° C、100° D、110°8. 如图,在△ABC中,∠B=50°,∠C=30°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,则∠BAD的度数为( )
A、120° B、105° C、100° D、110°8. 如图,在△ABC中,∠B=50°,∠C=30°,分别以点A和点C为圆心,大于 AC的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,则∠BAD的度数为( )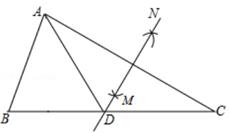 A、50° B、60° C、70° D、80°9. “如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A、50° B、60° C、70° D、80°9. “如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A、 B、 C、 D、10. 如图,在△ABC中,∠ABC=60°,∠C=45°,点D,E分别为边AB,AC上的点,且DE∥BC,BD=DE=2,CE= ,BC= .动点P从点B出发,以每秒1个单位长度的速度沿B→D→E→C匀速运动,运动到点C时停止.过点P作PQ⊥BC于点Q,设△BPQ的面积为S,点P的运动时间为t,则S关于t的函数图象大致为( )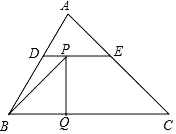 A、
A、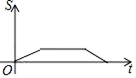 B、
B、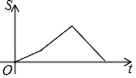 C、
C、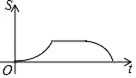 D、
D、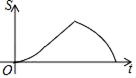
二、填空题
-
11. 计算:(π﹣3.14)0+3﹣1=.12. 关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是.13. 甲、乙、丙三名学生各自随机选择到A、B两个书店购书,则甲、乙、丙三名学生到同一个书店购书的概率为 .14. 如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,将Rt△AOB绕点O顺时针旋转90°后得到Rt△FOE,将线段EF绕点E逆时针旋转90°后得到线段ED,分別以O、E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分的面积是.
 15. 如图,矩形ABCD中,AB=4,AD=6,点E为AD中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为.
15. 如图,矩形ABCD中,AB=4,AD=6,点E为AD中点,点P为线段AB上一个动点,连接EP,将△APE沿PE折叠得到△FPE,连接CE,CF,当△ECF为直角三角形时,AP的长为.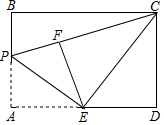
三、解答题
-
16. 先化简 ,然后从﹣1,0,2中选一个合适的x的值,代入求值。17. 某品牌牛奶供应商提供A,B,C,D四种不同口味的牛奶供学生饮用.某校为了了解学生对不同口味的牛奶的喜好,对全校订牛奶的学生进行了随机调查,并根据调查结果绘制了如下两幅不完整的统计图.
根据统计图的信息解决下列问题:
 (1)、本次调查的学生有多少人?(2)、补全上面的条形统计图;(3)、扇形统计图中C对应的中心角度数是;(4)、若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约多少盒?18. 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E.
(1)、本次调查的学生有多少人?(2)、补全上面的条形统计图;(3)、扇形统计图中C对应的中心角度数是;(4)、若该校有600名学生订了该品牌的牛奶,每名学生每天只订一盒牛奶,要使学生能喝到自己喜欢的牛奶,则该牛奶供应商送往该校的牛奶中,A,B口味的牛奶共约多少盒?18. 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E. (1)、求证:BE=EC(2)、填空:①若∠B=30°,AC=2 ,则DB=;
(1)、求证:BE=EC(2)、填空:①若∠B=30°,AC=2 ,则DB=;②当∠B=度时,以O,D,E,C为顶点的四边形是正方形.
19. 4月18日,一年一度的“风筝节”活动在市政广场举行,如图,广场上有一风筝A,小江抓着风筝线的一端站在D处,他从牵引端E测得风筝A的仰角为67°,同一时刻小芸在附近一座距地面30米高(BC=30米)的居民楼顶B处测得风筝A的仰角是45°,已知小江与居民楼的距离CD=40米,牵引端距地面高度DE=1.5米,根据以上条件计算风筝距地面的高度(结果精确到0.1米,参考数据:sin67°≈ ,cos67°≈ ,tan67°≈ , ≈1.414).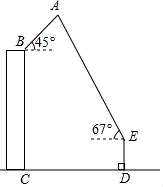 20. 如图,在平面直角坐标系xOy中,A(0,3),B(1,0),连接BA,将线段BA绕点B顺时针旋转90°得到线段BC,反比例函数y= 的图象G经过点C.
20. 如图,在平面直角坐标系xOy中,A(0,3),B(1,0),连接BA,将线段BA绕点B顺时针旋转90°得到线段BC,反比例函数y= 的图象G经过点C. (1)、请直接写出点C的坐标及k的值;(2)、若点P在图象G上,且∠POB=∠BAO,求点P的坐标;(3)、在(2)的条件下,若Q(0,m)为y轴正半轴上一点,过点Q作x轴的平行线与图象G交于点M,与直线OP交于点N,若点M在点N左侧,结合图象,直接写出m的取值范围.21. 某文具店经销甲、乙两种不同的笔记本.已知:两种笔记本的进价之和为10元,甲种笔记本每本获利2元,乙种笔记本每本获利1元,马阳光同学买4本甲种笔记本和3本乙种笔记本共用了47元.(1)、甲、乙两种笔记本的进价分别是多少元?(2)、该文具店购入这两种笔记本共60本,花费不超过296元,则购买甲种笔记本多少本时该文具店获利最大?(3)、店主经统计发现平均每天可售出甲种笔记本350本和乙种笔记本150本.如果甲种笔记本的售价每提高1元,则每天将少售出50本甲种笔记本;如果乙种笔记本的售价每提高1元,则每天少售出40本乙种笔记本,为使每天获取的利润更多,店主决定把两种笔记本的价格都提高 元,在不考虑其他因素的条件下,当 定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?22.
(1)、请直接写出点C的坐标及k的值;(2)、若点P在图象G上,且∠POB=∠BAO,求点P的坐标;(3)、在(2)的条件下,若Q(0,m)为y轴正半轴上一点,过点Q作x轴的平行线与图象G交于点M,与直线OP交于点N,若点M在点N左侧,结合图象,直接写出m的取值范围.21. 某文具店经销甲、乙两种不同的笔记本.已知:两种笔记本的进价之和为10元,甲种笔记本每本获利2元,乙种笔记本每本获利1元,马阳光同学买4本甲种笔记本和3本乙种笔记本共用了47元.(1)、甲、乙两种笔记本的进价分别是多少元?(2)、该文具店购入这两种笔记本共60本,花费不超过296元,则购买甲种笔记本多少本时该文具店获利最大?(3)、店主经统计发现平均每天可售出甲种笔记本350本和乙种笔记本150本.如果甲种笔记本的售价每提高1元,则每天将少售出50本甲种笔记本;如果乙种笔记本的售价每提高1元,则每天少售出40本乙种笔记本,为使每天获取的利润更多,店主决定把两种笔记本的价格都提高 元,在不考虑其他因素的条件下,当 定为多少元时,才能使该文具店每天销售甲、乙两种笔记本获取的利润最大?22. (1)、观察猜想
(1)、观察猜想如图①点B、A、C在同一条直线上,DB⊥BC,EC⊥BC且∠DAE=90°,AD=AE,则BC、BD、CE之间的数量关系为;
(2)、问题解决如图②,在Rt△ABC中,∠ABC=90°,CB=4,AB=2,以AC为直角边向外作等腰Rt△DAC,连结BD,求BD的长;
(3)、拓展延伸如图③,在四边形ABCD中,∠ABC=∠ADC=90°,CB=4,AB=2,DC=DA,请直接写出BD的长.
23. 抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3). (1)、求抛物线的解析式;(2)、如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;(3)、如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
(1)、求抛物线的解析式;(2)、如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;(3)、如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.