河南省信阳市2019届九年级普通高中招生模拟考试(一)数学试卷
试卷更新日期:2020-01-15 类型:中考模拟
一、单选题
-
1. 实数 在数轴上对应的点的位置如图所示,这四个数中最大的是( )
 A、 B、 C、 D、2. 2018年4月10日,历时四个月的“2018中国茶叶区域公用品牌价值评估”结果出炉,信阳毛尖较去年增加3.61亿元,以63.52亿元蝉联品牌价值排行榜第二名,并被评选为“最具品牌带动力”的三大品牌之一.数据63.52亿元用科学记数法表示为( )A、 B、 C、 D、3. 如图,是一个正方体的表面展开图,则原正方体中“学”字所在的面相对的面上标的字是( )
A、 B、 C、 D、2. 2018年4月10日,历时四个月的“2018中国茶叶区域公用品牌价值评估”结果出炉,信阳毛尖较去年增加3.61亿元,以63.52亿元蝉联品牌价值排行榜第二名,并被评选为“最具品牌带动力”的三大品牌之一.数据63.52亿元用科学记数法表示为( )A、 B、 C、 D、3. 如图,是一个正方体的表面展开图,则原正方体中“学”字所在的面相对的面上标的字是( ) A、我 B、是 C、优 D、生4. 下列运算正确的是A、 B、 C、 D、5. 如图所示是小明在某条道路所统计的某个时段来往车辆的车速情况,下列说法中正确的是( )
A、我 B、是 C、优 D、生4. 下列运算正确的是A、 B、 C、 D、5. 如图所示是小明在某条道路所统计的某个时段来往车辆的车速情况,下列说法中正确的是( ) A、中位数是52.5 B、众数是8 C、众数是52 D、中位数是536. “算经十书”是指汉唐一千多年间的十部著名数学著作,它们曾经是隋唐时期国子监算学科的教科书,这些流传下来的古算书中凝聚着历代数学家的劳动成果.下列四部著作中,不属于我国古代数学著作的是( )
A、中位数是52.5 B、众数是8 C、众数是52 D、中位数是536. “算经十书”是指汉唐一千多年间的十部著名数学著作,它们曾经是隋唐时期国子监算学科的教科书,这些流传下来的古算书中凝聚着历代数学家的劳动成果.下列四部著作中,不属于我国古代数学著作的是( )
A、 B、
B、 C、
C、 D、
D、 7. 关于 的一元二次方程 没有实数根,则整数 的最小值是( )A、0 B、1 C、2 D、38. 点P的坐标是(m,n),从﹣5,﹣3,0,4,7这五个数中任取一个数作为m的值,再从余下的四个数中任取一个数作为n的值,则点P(m,n)在平面直角坐标系中第二象限内的概率是( )A、 B、 C、 D、9. 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2x,y+1),则y关于x的函数关系为( )
7. 关于 的一元二次方程 没有实数根,则整数 的最小值是( )A、0 B、1 C、2 D、38. 点P的坐标是(m,n),从﹣5,﹣3,0,4,7这五个数中任取一个数作为m的值,再从余下的四个数中任取一个数作为n的值,则点P(m,n)在平面直角坐标系中第二象限内的概率是( )A、 B、 C、 D、9. 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2x,y+1),则y关于x的函数关系为( )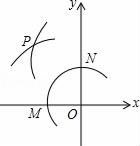 A、y=x B、y=﹣2x﹣1 C、y=2x﹣1 D、y=1﹣2x10. 如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )
A、y=x B、y=﹣2x﹣1 C、y=2x﹣1 D、y=1﹣2x10. 如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )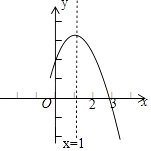 A、①②④ B、①②⑤ C、②③④ D、③④⑤
A、①②④ B、①②⑤ C、②③④ D、③④⑤二、填空题
-
11. 计算: 。12. 如图,在平行线 之间放置一块直角三角板,三角板的锐角顶点 分别在直线 上,若 ,则 的度数是.
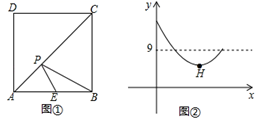
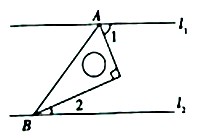 13. 如果不等式组 的解集是 ,那么 的值是.14. 如图①,在正方形 中,点 是 的中点,点 是对角线 上一动点,设 的长度为 与 的长度和为 ,图②是 关于 的函数图象,则图象上最低点 的坐标为.
13. 如果不等式组 的解集是 ,那么 的值是.14. 如图①,在正方形 中,点 是 的中点,点 是对角线 上一动点,设 的长度为 与 的长度和为 ,图②是 关于 的函数图象,则图象上最低点 的坐标为.
 15. 如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为点D′,若CD′垂直于菱形ABCD的边时,则DE的长为.
15. 如图,四边形ABCD是菱形,AB=2,∠ABC=30°,点E是射线DA上一动点,把△CDE沿CE折叠,其中点D的对应点为点D′,若CD′垂直于菱形ABCD的边时,则DE的长为.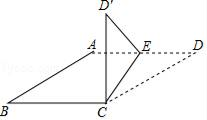
三、解答题 三、解答题
-
16. 先化简,再求值: ,其中 .17. 雾霾天气严重影响市民的生活质量。在今年寒假期间,某校九年级一班的综合实践小组学生对“雾霾天气的主要成因”随机调查了所在城市部分市民,并对调查结果进行了整理,绘制了下图所示的不完整的统计图表:
组别
雾霾天气的主要成因
百分比
A
工业污染
45%
B
汽车尾气排放
C
炉烟气排放
15%
D
其他(滥砍滥伐等)
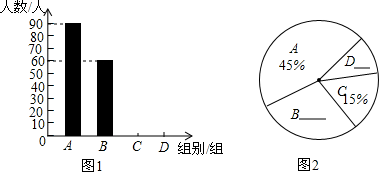
请根据统计图表回答下列问题:
(1)、本次被调查的市民共有多少人?并求 和 的值;(2)、请补全条形统计图,并计算扇形统计图中扇形区域 所对应的圆心角的度数;(3)、若该市有100万人口,请估计市民认为“工业污染和汽车尾气排放是雾霾天气主要成因”的人数.18. 如图,在平面直角坐标系 中,一次函数 的图象经过点 ,与反比例函数 的图象交于 .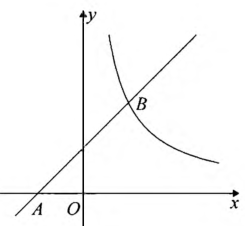 (1)、求一次函数和反比例函数的表达式;(2)、设 是直线 上一点,过 作 轴,交反比例函数 的图象于点 ,若 为顶点的四边形为平行四边形,求点 的坐标.19. 如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OF⊥AB,交AC于点F,点E在AB的延长线上,射线EM经过点C,且∠ACE+∠AFO=180°.
(1)、求一次函数和反比例函数的表达式;(2)、设 是直线 上一点,过 作 轴,交反比例函数 的图象于点 ,若 为顶点的四边形为平行四边形,求点 的坐标.19. 如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OF⊥AB,交AC于点F,点E在AB的延长线上,射线EM经过点C,且∠ACE+∠AFO=180°.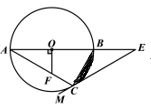 (1)、求证:EM是⊙O的切线;(2)、若∠A=∠E,BC= ,求阴影部分的面积.(结果保留 和根号).20. 茗阳阁位于河南省信阳市狮河区茶韵路一号,建成于2007年4月29日.是一栋由多种中国建筑元素,由雕栏飞檐、勾心斗角、斗拱图腾等多种形式的中国古代建筑元素汇聚而成,具有浓郁地方古建筑特色的塔式阁楼.茗阳阁是信阳新建的城市文化与形象的代表建筑之一,同时茗阳阁旁的风景也是优美至极.某数学课外兴趣小组为了测量建在山丘 上的茗阳阁 的高度,在山脚下的广场上 处测得建筑物点 (即山顶)的仰角为20°,沿水平方向前进20米到达 点,测得建筑物顶部 点的仰角为45°,已知山丘 高37.69米.求塔的高度 .(结果精确到1米,参考数据: )
(1)、求证:EM是⊙O的切线;(2)、若∠A=∠E,BC= ,求阴影部分的面积.(结果保留 和根号).20. 茗阳阁位于河南省信阳市狮河区茶韵路一号,建成于2007年4月29日.是一栋由多种中国建筑元素,由雕栏飞檐、勾心斗角、斗拱图腾等多种形式的中国古代建筑元素汇聚而成,具有浓郁地方古建筑特色的塔式阁楼.茗阳阁是信阳新建的城市文化与形象的代表建筑之一,同时茗阳阁旁的风景也是优美至极.某数学课外兴趣小组为了测量建在山丘 上的茗阳阁 的高度,在山脚下的广场上 处测得建筑物点 (即山顶)的仰角为20°,沿水平方向前进20米到达 点,测得建筑物顶部 点的仰角为45°,已知山丘 高37.69米.求塔的高度 .(结果精确到1米,参考数据: )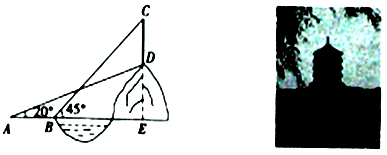 21. 每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买了3台甲型设备比购买2台乙型设备多花了16万元,购买2台甲型设备比购买3台乙型设备少花6万元.(1)、求甲、乙两种型号设备的价格;(2)、该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有几种购买方案;(3)、在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月,若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.22. 如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
21. 每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买了3台甲型设备比购买2台乙型设备多花了16万元,购买2台甲型设备比购买3台乙型设备少花6万元.(1)、求甲、乙两种型号设备的价格;(2)、该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有几种购买方案;(3)、在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月,若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.22. 如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.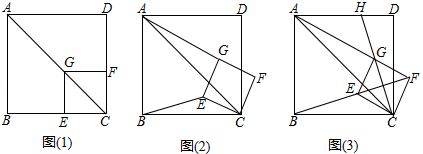 (1)、证明与推断:
(1)、证明与推断:①求证:四边形CEGF是正方形;
②推断: 的值。
(2)、探究与证明:将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)、拓展与运用:正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2 ,则BC=.
23. 如图所示,已知抛物线y=ax2+bx+c(a≠0)经过点A(﹣2,0)、B(4,0)、C(0,﹣8),与直线y=x﹣4交于B,D两点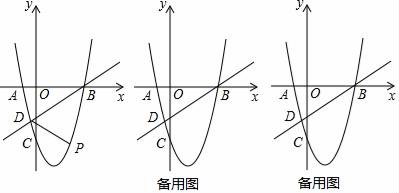 (1)、求抛物线的解析式并直接写出D点的坐标;(2)、点P为直线BD下方抛物线上的一个动点,试求出△BDP面积的最大值及此时点P的坐标;(3)、点Q是线段BD上异于B、D的动点,过点Q作QF⊥x轴于点F,交抛物线于点G,当△QDG为直角三角形时,直接写出点Q的坐标.
(1)、求抛物线的解析式并直接写出D点的坐标;(2)、点P为直线BD下方抛物线上的一个动点,试求出△BDP面积的最大值及此时点P的坐标;(3)、点Q是线段BD上异于B、D的动点,过点Q作QF⊥x轴于点F,交抛物线于点G,当△QDG为直角三角形时,直接写出点Q的坐标.