河南省新乡市2019届九年级数学中考模拟试卷

试卷更新日期：2020-01-15 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，绝对值最小的数是（）

A、π B、 $\frac{1}{2}$ C、-2 D、- $\frac{1}{3}$

查看试题解析
2. 某市交通一卡通已经覆盖了全市的地面公交、轨道交通和部分出租车及停车场.据某市交通委透露，某市政交通一卡通卡发卡量目前已经超过280000000张，用科学记数法表示280000000正确是（　　）

A、2.8×10⁷ B、2.8×10⁸ C、2.8×10⁹ D、0.28×10¹⁰

查看试题解析
3.
如图，是一个几何体的三视图，根据图中标注的数据可求得这个几何体的体积为（）

A、12π B、24π C、36π D、48π

查看试题解析
4. 已知一次函数y=kx+b中，x取不同值时，y对应的值列表如下：则不等式kx+b＞0（其中k，b，m，n为常数）的解集为（）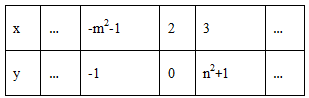

A、x＞2 B、x＞3 C、x＜2 D、无法确定

查看试题解析
5. 某校举行健美操比赛，甲、乙两班个班选20名学生参加比赛，两个班参赛学生的平均身高都是1.65米，其方差分别是 $s_{甲}^{2} = 1.9 ， s_{乙}^{2} = 2.4$ ，则参赛学生身高比较整齐的班级是( ）

A、甲班 B、乙班 C、同样整齐 D、无法确定

查看试题解析
6. 如图，四边形ABCD内接于⊙O，E是BC延长线上一点，下列等式中不一定成立的是（）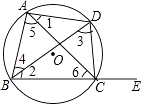

A、∠1=∠2 B、∠3=∠5 C、∠BAD=∠DCE D、∠4=∠6

查看试题解析
7. 平面内有一个角是60°的菱形绕它的中心旋转，使它与原来的菱形重合，那么旋转的角度至少是（）

A、90° B、180° C、270° D、360°

查看试题解析
8. 如图，将矩形ABCD沿AE折叠，点D的对应点落在BC上点F处，过点F作FG∥CD，连接EF，DG，下列结论中正确的有（）
①∠ADG=∠AFG；②四边形DEFG是菱形；③DG²= $\frac{1}{2}$ AE•EG；④若AB=4，AD=5，则CE=1．

A、①②③④ B、①②③ C、①③④ D、①②

查看试题解析
9. 将二次函数y=3x²的图象向右平移3个单位，再向下平移4个单位后，所得图象的函数表达式是（）

A、y=3（x-3）²-4 B、y=3（x-3）²+4 C、y=3（x+3）²-4 D、y=3（x+3）²+4

查看试题解析
10. 在正方形ABCD中，对角线AC=BD=12cm，点P为AB边上的任一点，则点P到AC，BD的距离之和为（　　）

A、6cm B、7cm C、6 $\sqrt{2}$ cm D、12 $\sqrt{2}$ cm

查看试题解析

二、填空题

11. 计算：（ $\sqrt{2}$ +π）⁰﹣2|1﹣sin30°|+（ $\frac{1}{2}$ ）^﹣¹= ．

查看试题解析
12. 若关于x的一元二次方程 $k x^{2} + 2 (k + 1) x + k - 1 = 0$ 有两个不相等的实数根，则k的取值范围是.

查看试题解析
13.
如图，已知点A在反比例函数y= $\frac{k}{x}$ （x＜0）上，作Rt△ABC，点D为斜边AC的中点，连DB并延长交y轴于点E．若△BCE的面积为8，则k= ．

查看试题解析
14. 二次函数 $y = 2 x^{2} - 1$ ，∵ $a =$ ， ∴函数有最值.

查看试题解析
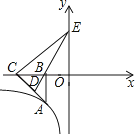15. 如图，在Rt△ABC中，∠B＝90°，AB＝3，BC＝4，将△ABC折叠，使点B恰好落在边AC上，与点B′重合，AE为折痕，则EB′＝.

查看试题解析

三、解答题

16. 先化简，再求值： $\frac{a^{2} - b^{2}}{a} \div (\frac{2 a b - b^{2}}{a} - a)$ ，其中a=1+ $\sqrt{3}$ ，b=1- $\sqrt{3}$ .

查看试题解析
17. 课外阅读是提高学生素养的重要途径，亚光初中为了了解学校学生的阅读情况，组织调查组对全校三个年级共1500名学生进行了抽样调查，抽取的样本容量为300。已知该校有初一学生600名，初二学生500名，初三学生400名。

(1)、为使调查的结果更加准确地反映全校的总体情况，应分别在初一年级随机抽取人；在初二年级随机抽取人；在初三年级随机抽取人（请直接填空）。

(2)、调查组对本校学生课外阅读量的统计结果分别用扇形统计图和频数分布直方图表示如下，请根据上统计图，计算样本中各类阅读量的人数，并补全频数分布直方图。

(3)、根据（2）的调查结果，从该校中随机抽取一名学生，他最大可能的阅读量是多少本？为什么？

查看试题解析
18. 已知：如图，在菱形ABCD中，F为边BC的中点，DF与对角线AC交于点M，过M作ME⊥CD于点E，∠1=∠2．

(1)、若CE=1，求BC的长；

(2)、求证：AM=DF+ME．

查看试题解析
19. 2014年3月，某海域发生航班失联事件，我海事救援部门用高频海洋探测仪进行海上搜救，分别在A、B两个探测点探测到C处是信号发射点，已知A、B两点相距400m，探测线与海平面的夹角分别是 $30^{\circ}$ 和 $60^{\circ}$ ，若CD的长是点C到海平面的最短距离.

(1)、问BD与AB有什么数量关系，试说明理由；

(2)、求信号发射点的深度 $. ($ 结果精确到1m，参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732)$

查看试题解析
20. 列方程（或方程组）解应用题：

(1)、某服装店到厂家选购甲、乙两种服装，若购进甲种服装9件、乙种服装10件，需1810元；购进甲种服装11件乙种服装8件，需1790元，求甲乙两种服装每件价格相差多少元？

(2)、某工厂现库存某种原料1200吨，用来生产A、B两种产品，每生产1吨A产品需这种原料2吨、生产费用1000元；每生产1吨B产品需这种原料2.5吨、生产费用900元，如果用来生产这两种产品的资金为53万元，那么A、B两种产品各生产多少吨才能使库存原料和资金恰好用完？

查看试题解析
21. 已知二次函数y=﹣x²+4x．

(1)、写出二次函数y=﹣x²+4x图象的对称轴；

(2)、在给定的平面直角坐标系中，画出这个函数的图象（列表、描点、连线）；

(3)、根据图象，写出当y＜0时，x的取值范围．

查看试题解析
22. 如图，在▱ABCD中，AE=CF．

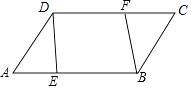(1)、求证：△ADE≌△CBF；

(2)、求证：四边形BFDE为平行四边形．

查看试题解析
23. 如图，抛物线y＝－x ²＋bx＋c与x轴交于A、B两点，与y轴交于点C，已知经过B、C两点的直线的表达式为y＝－x＋3．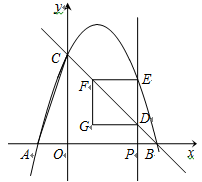

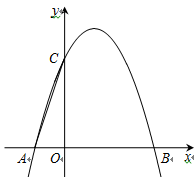(1)、求抛物线的函数表达式；

(2)、点P(m，0)是线段OB上的一个动点，过点P作y轴的平行线，交直线BC于D，交抛物线于E，EF∥x轴，交直线BC于F，DG∥x轴，FG∥y轴，DG与FG交于点G．设四边形DEFG的面积为S，当m为何值时S最大，最大值是多少？

(3)、在坐标平面内是否存在点Q，将△OAC绕点Q逆时针旋转90°，使得旋转后的三角形恰好有两个顶点落在抛物线上．若存在，求出所有符合条件的点Q的坐标；若不存在，请说明理由．

查看试题解析