2016-2017学年安徽省宿州市高一下学期期末数学试卷

试卷更新日期：2017-08-04 类型：期末考试

进入出卷网下载

一、一.选择题

1. 若a＜b＜0，则下列不等式中不能成立的是（）

A、 $\frac{1}{a}$ ＞ $\frac{1}{b}$ B、 $\frac{1}{a - b}$ ＞ $\frac{1}{a}$ C、|a|＞|b| D、a²＞b²

查看试题解析
2. 数列 $\frac{3}{2}$ ，﹣ $\frac{5}{4}$ ， $\frac{7}{8}$ ，﹣ $\frac{9}{16}$ ，…的一个通项公式为（）

A、a_n=（﹣1）ⁿ $\frac{2^{n} - 1}{2^{n}}$ B、a_n=（﹣1）ⁿ $\frac{2^{n} + 1}{2^{n}}$ C、a_n=（﹣1）ⁿ⁺¹ $\frac{2^{n} - 1}{2^{n}}$ D、a_n=（﹣1）ⁿ⁺¹ $\frac{2^{n} + 1}{2^{n}}$

查看试题解析
3. 从学号为1～50的高一某班50名学生中随机选取5名同学参加数学测试，采用系统抽样的方法，则所选5名学生的学号可能是（）

A、3，11，19，27，35 B、5，15，25，35，46 C、2，12，22，32，42 D、4，11，18，25，32

查看试题解析
4. 等差数列{a_n}中，a₄=﹣8，a₈=2，则a₁₂=（）

A、10 B、12 C、14 D、16

查看试题解析
5. 甲、乙、丙是同班同学，假设他们三个人早上到学校先后的可能性是相同的，则事件“甲比乙先到学校，乙又比丙先到学校”的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
6. 下列命题中，正确的是（）

A、函数y=x+ $\frac{1}{x}$ 的最小值为2 B、函数y= $\frac{x^{2} + 3}{\sqrt{x^{2} + 2}}$ 的最小值为2 C、函数y=2﹣x﹣ $\frac{4}{x}$ （x＞0）的最大值为﹣2 D、函数y=2﹣x﹣ $\frac{4}{x}$ （x＞0）的最小值为﹣2

查看试题解析
7. 不等式 $\frac{x}{x - 1}$ ≥﹣1的解集为（）

A、（﹣∞， $\frac{1}{2}$ ]∪（1，+∞） B、[ $\frac{1}{2}$ ，+∞） C、[ $\frac{1}{2}$ ，1）∪（1，+∞） D、（﹣∞， $\frac{1}{2}$ ]∪[1，+∞）

查看试题解析
8. 某小组有3名男生和2名女生，从中任选2名同学参加演讲比赛，那么互斥不对立的两个事件是（　　）

A、恰有1名男生与恰有2名女生 B、至少有1名男生与全是男生 C、至少有1名男生与至少有1名女生 D、至少有1名男生与全是女生

查看试题解析
9. 在△ABC中，角A，B，C的对边分别是a，b，c，若a²﹣b²= $\sqrt{3}$ bc，sinC=2 $\sqrt{3}$ sinB，则A=（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{2 π}{3}$ D、 $\frac{5 π}{6}$

查看试题解析
10. 已知甲、乙两组数据的茎叶如图所示，若它们的平均数相同，则下列关于甲、乙两组数据稳定性的描述，正确的是（）

A、甲较稳定 B、乙较稳定 C、二者相同 D、无法判断

查看试题解析
11. 某程序框图如图所示，该程序运行后输出的k的值是（）

A、3 B、4 C、5 D、6

查看试题解析
12. 宿州市某登山爱好者为了解山高y（百米）与气温x（℃）之间的关系，随机统计了4次山高与相应的气温，并制作了对照表，由表中数据，得到线性回归方程为y=﹣2x+a，由此估计山高为72（百米）处的气温为（）
气温x（℃）
18
13
10
﹣1
山高y（百米）
24
34
38
64

A、﹣10 B、﹣8 C、﹣6 D、﹣4

查看试题解析

二、二.填空题

13. 数列{a_n}中，若a_n= ${\begin{matrix} 2 n - 1 ， n 为奇数 \\ 2^{n} ， n 为偶数 \end{matrix}$ ，则其前6项和为．

查看试题解析
14. 如果实数x，y满足约束条件 ${\begin{matrix} x + y + 1 \leq 0 \\ x - y + 1 \geq 0 \\ y \geq - 1 \end{matrix}$ ，那么目标函数z=2x﹣y的最小值为．

查看试题解析
15. 如图所示，为了求出一个边长为10的正方形内的不规则图形的面积，小明设计模拟实验：向这个正方形内均匀的抛洒20粒芝麻，结果有8粒落在了不规则图形内，则不规则图形的面积为．

查看试题解析
16. 为响应国家治理环境污染的号召，增强学生的环保意识，宿州市某中学举行了一次环保知识竞赛，共有900名学生参加了这次竞赛，为了解本次竞赛的成绩情况，从中抽取了l00学生的成绩进行统计，成绩频率分布直方图如图所示．估计这次测试中成绩的众数为；平均数为；中位数为．（各组平均数取中值计算，保留整数）

查看试题解析

三、三.解答题

17. 苏州市一木地板厂生产A、B、C三类木地板，每类木地板均有环保型和普通两种型号，某月的产量如下表（单位：片）：
类型
木地板A
木地板B
木地板C
环保型
150
200
Z
普通型
250
400
600
按分层抽样的方法在这个月生产的木地板中抽取50片，其中A类木地板10片．

(1)、求Z的值；

(2)、用随机抽样的方法从B类环保木地板抽取8片，作为一个样本，经检测它们的得分如下：9.4、8.6、9.2、9.6、8.7、9.3、9.0、8.2，从中任取一个数，求该数与样本平均数之差的绝对不超过0.5的概率．

查看试题解析
18. 函数f（x）=x²+ax+3，已知不等式f（x）＜0的解集为{x|1＜x＜3}．

(1)、求a；

(2)、若不等式f（x）≥m的解集是R，求实数m的取值范围；

(3)、若f（x）≥nx对任意的实数x≥1成立，求实数n的取值范围．

查看试题解析
19. 宿州某中学N名教师参加“低碳节能你我他”活动，他们的年龄在25岁至50岁之间，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示．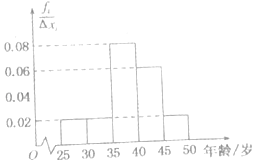
下表是年龄的频数分布表：
区间
[25，30）
[30，35）
[35，40）
[40，45）
[45，50]
人数
25
m
p
75
25

(1)、求正整数m，p，N的值；

(2)、用分层抽样的方法，从第1、3、5组抽取6人，则第1、3、5组各抽取多少人？

(3)、在（2）的条件下，从这6人中随机抽取2人参加学校之间的宣传交流活动，求恰有1人在第3组的概率．

查看试题解析
20. 判断居民户是否小康的一个重要指标是居民户的年收入，某市从辖区内随机抽取100个居民户，对每个居民户的年收入与年结余的情况进行分析，设第i个居民户的年收入x_i（万元），年结余y_i（万元），经过数据处理的： $\sum_{i = 1}^{100} x_{i}$ =400， $\sum_{i = 1}^{100} y_{i}$ =100， $\sum_{i = 1}^{100} x_{i} y_{i}$ =900， $\sum_{i = 1}^{100} x^{2}_{i}$ =2850．

(1)、已知家庭的年结余y对年收入x具有线性相关关系，求线性回归方程；

(2)、若该市的居民户年结余不低于5万，即称该居民户已达小康生活，请预测居民户达到小康生活的最低年收入应为多少万元？
附：在y=bx+a中，b= $\frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x^{2}_{i} - n {\bar{x}}^{2}}$ ，a= $\bar{y} - b \bar{x}$ ，其中 $\bar{x}$ ， $\bar{y}$ 为样本平均值．

查看试题解析
21. 在△ABC中，内角A，B，C所对的边分别是a，b，c．

(1)、若a=2 $\sqrt{3}$ ，A= $\frac{π}{3}$ ，且△ABC的面积S=2 $\sqrt{3}$ ，求b，c的值；

(2)、若sin（C﹣B）=sin2B﹣sinA，试判断△ABC的形状．

查看试题解析
22. 已知数列{a_n₊₁﹣2a_n}是公比为2的等比数列，其中a₁=1，a₂=4．

(1)、证明：数列{ $\frac{a_{n}}{2^{n}}$ }是等差数列；

(2)、求数列{a_n}的前n项和S_n；

(3)、记C_n= $\frac{2 a_{n} - 2 n}{n}$ （n≥2），证明： $\frac{1}{2} -$ （ $\frac{1}{2}$ ）ⁿ＜ $\frac{1}{c_{2}} + \frac{1}{c_{3}}$ +…+ $\frac{1}{c_{n}}$ ≤1﹣（ $\frac{1}{2}$ ）ⁿ^﹣¹ ．

查看试题解析

类型	木地板A	木地板B	木地板C
环保型	150	200	Z
普通型	250	400	600

区间	[25，30）	[30，35）	[35，40）	[40，45）	[45，50]
人数	25	m	p	75	25

气温x（℃）	18	13	10	﹣1
山高y（百米）	24	34	38	64