江苏省无锡市锡北片2020届九年级上学期数学期中考试试卷

试卷更新日期：2020-01-15 类型：期中考试

进入 出卷网 下载

一、选择题

  • 1. 下列方程是一元二次方程的是（   ）
    A、3x2－6x+2 B、x2-y+1=0 C、x2=0 D、1x2 + x=2

    查看试题解析

  • 2. 方程3x2+4x﹣2=0根的情况是（    ）
    A、两个不相等的实数根 B、两个相等的实数根 C、没有实数根 D、无法确定

    查看试题解析

  • 3. 如图，在△ABC中，DE∥BC，若 ADAB = 13 ，DE＝4，则BC的值为（   ）

    A、9 B、10 C、11 D、12

    查看试题解析

  • 4. 如图，已知∠1＝∠2，那么添加下列一个条件后，仍无法判定△ABC∽△ADE的是（   ）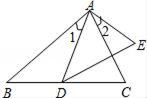

    A、∠C＝∠E B、∠B＝∠ADE C、ABAD=ACAE D、ABAD=BCDE

    查看试题解析

  • 5. 如图，在长为100 m，宽为80 m的矩形场地上修建两条宽度相等且互相垂直的道路，剩余部分进行绿化，要使绿化面积为7644m2 ， 则道路的宽应为多少米？设道路的宽为x m，则可列方程为 （ ）

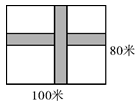    A、100×80－100x－80x=7644 B、(100－x)(80－x)＋x2=7644 C、(100－x)(80－x)=7644 D、100x＋80x－x2=7644

    查看试题解析

  • 6. 如图所示，已知四边形ABDC是圆内接四边形，∠1=112°，则∠CDE=（   ）

    A、56° B、68° C、66° D、58°

    查看试题解析

  • 7. 如图，为了测量某棵树的高度，小明用长为2m的竹竿作测量工具，移动竹竿，使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点．此时竹竿与这一点相距5m，与树相距10m，则树的高度为（   ）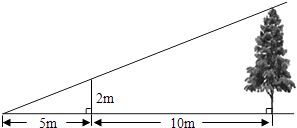

    A、5m B、6m C、7m D、8m

    查看试题解析

  • 8. 如图，AB，AC是⊙O的两条弦，∠BAC=25°，过点C的切线与OB的延长线交于点D，则∠D的度数为（   ）

    A、25° B、30° C、35° D、40°

    查看试题解析

  • 9. 如图，平行四边形ABCD对角线AC与BD交于点O，且AD＝6，AB＝10，在AB延长线上取一点E，使BE＝ 25 AB，连接OE交BC于F，则BF的长为（　　）

    A、23 B、43 C、65 D、1

    查看试题解析

  • 10. 如图，线段AB为⊙O的直径，点C在AB的延长线上，AB＝4，BC＝2，点P是⊙O上一动点，连接CP，以CP为斜边在PC的上方作Rt△PCD，且使∠DCP＝60°，连接OD，则OD长的最大值为 (    ）

    A、 B、 C、 D、4

    查看试题解析

二、填空题

  • 11. 将一元二次方程5x(x－3)=1化成一般形式为

    查看试题解析

  • 12. 一元二次方程 的根是.

    查看试题解析

  • 13. 已知：一元二次方程x2-6x+c=0有一个根为2，则另一根为。

    查看试题解析

  • 14. 已知圆锥的底面半径为4cm，母线长为5cm，则圆锥的侧面积是

    查看试题解析

  • 15. △ABC与△A′B′C′是位似图形，且△ABC与△A′B′C′的位似比是1：2，已知△ABC的面积是3，则△A′B′C′的面积是.

    查看试题解析

  • 16. 把球放在长方体纸盒内，球的一部分露出盒外，其主视图如图．⊙O与矩形ABCD的边BC，AD分别相切和相交（E，F是交点），已知EF=CD=8，则⊙O的半径为 ．

    查看试题解析

  • 17. 如图，A是半径为2的⊙O外的一点，OA＝4，AB切⊙O于点B，弦BC∥OA，连接AC，则图中阴影部分的面积为

    查看试题解析

  • 18. 如图，在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，点E从C点出发向终点B运动，速度为1cm/秒，运动时间为t秒，作EF∥AB，点P是点C关于FE的对称点，连接AP，当△AFP恰好是直角三角形时，t的值为

    查看试题解析

三、解答题

  • 19. 用适当的方法解下列方程：
    (1)、（x-1）2﹣9＝0;
    (2)、3（x+5）=（x+5）2；
    (3)、x2＋6x－55＝0；
    (4)、2x(x＋3)－1＝0.

    查看试题解析

  • 20. 如图，在□ABCD中，点E在BC上，∠CDE＝∠DAE.

    (1)、求证：△ADE∽△DEC；
    (2)、若AD＝6，DE＝4，求BE的长.

    查看试题解析

  • 21. 如图，线段AB的端点在边长为1的正方形网格的格点上，现将线段AB绕点A按逆时针方向旋转90°得到线段AC．

    (1)、请你用直尺和圆规在所给的网格中画出线段AC及点B经过的路径；
    (2)、若将此网格放在一平面直角坐标系中，已知点A的坐标为

    （1，3），点B的坐标为（﹣2，﹣1），则点C的坐标为；

    (3)、线段AB在旋转到线段AC的过程中，点B经过的路径长为；
    (4)、若有一张与（3）中所说的区域形状相同的纸片，将它围成个圆锥的侧面，则该圆锥底面圆的半径长为 ．

    查看试题解析

  • 22. 已知关于x的方程x2+（2m+1）x+m（m+1）＝0.
    (1)、求证：方程总有两个不相等的实数根；
    (2)、已知方程的一个根为x＝0，求代数式m2+m﹣5的值.

    查看试题解析

  • 23. 如图，△ABC中，AB=AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，过点D作DF⊥AC于点F.

    (1)、试说明DF是⊙O的切线；
    (2)、若AC=3AE=6，求tanC

    查看试题解析

  • 24. 长城汽车销售公司5月份销售某种型号汽车，当月该型号汽车的进价为30万元/辆，若当月销售量超过5辆时，每多售出1辆，所有售出的汽车进价均降低0.1万元/辆．根据市场调查，月销售量不会突破30台．
    (1)、设当月该型号汽车的销售量为x辆（x≤30，且x为正整数），实际进价为y万元/辆，求y与x的函数关系式；
    (2)、已知该型号汽车的销售价为32万元/辆，公司计划当月销售利润45万元，那么该月需售出多少辆汽车？（注：销售利润=销售价﹣进价）

    查看试题解析

  • 25. 如图所示，AC⊥AB， 3≤n≤12 ，AC=2，点D是以AB为直径的半圆O 上一动点，DE⊥CD交直线AB于点E，设 ∠DAB=α(0°<α<90°) .

    (1)、当 α=20∘ 时，求弧BD的长；
    (2)、当 α=30° 时，求线段BE的长；
    (3)、若要使点E在线段BA的延长线上，求 α 的取值范围.(直接写出答案)

    查看试题解析

  • 26. 如图1，在Rt△ABC中，∠ABC＝90°，AB＝BC＝4，点D、E分别是边AB、AC的中点，连接DE，将△ADE绕点A按顺时针方向旋转，记旋转角为α，BD、CE所在直线相交所成的锐角为β.

    (1)、问题发现：当α＝0°时， CEBD ＝；β＝°.
    (2)、拓展探究：试判断：当0°≤α＜360°时， CEBD 和β的大小有无变化？请仅就图2的情形给出证明.
    (3)、在△ADE旋转过程中，当DE∥AC时，直接写出此时△CBE的面积.

    查看试题解析

  • 27. 在平面直角坐标系xOy中，⊙C的半径为r，P是与圆心C不重合的点，点P关于⊙C的发散点的定义如下：若在射线CP上存在一点P′，满足CP＋CP′＝3r，则称P′为点P关于⊙C的发散点.下图为点P及其关于⊙C的发散点P′的示意图.特别地，当点P′与圆心C重合时，规定CP′＝0.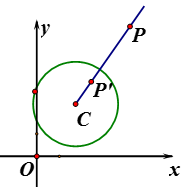

    根据上述材料，请你解决以下问题：

    (1)、当⊙O的半径为1时，

    ①在点 M（3 ， 1） ， N(32 ， 0） ， T(22 ， 1） 中存在关于⊙O的发散点的是点；其对应发散点的坐标是；

    ②点P在直线 y=−3x+33 上，若点P关于⊙O的发散点P′存在，且点P′不在x轴上，求点P的横坐标m的取值范围

    (2)、⊙C的圆心C在x轴上，半径为1，直线 y=−33x+33 与x轴、y轴分別交于点A，B.若线段AB上存在点P，使得点P关于⊙C的发散点P′在⊙C的内部，请直接写出圆心C的横坐标n的取值范围.

    查看试题解析