湖北省宜昌市东部2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-01-15 类型:期中考试
一、单选题
-
1. 下列方程中,是关于x的一元二次方程的是( ).A、ax2+bx+c=0 B、x(x-2)=0 C、 D、2. 一元二次方程 的二次项系数和一次项系数分别为( )A、3,-1 B、3,-4 C、3,4 D、 ,3. 方程 的解是( )A、 B、 , C、 , D、4. 下列图形中,既是轴对称图形又是中心对称图形的是A、
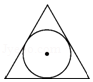 B、
B、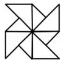 C、
C、 D、
D、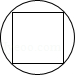 5. 若方程x2-4x+m=0有两个相等的实数根,则m的值是( ).A、4 B、-4 C、 D、6. 函数y=x2-2x+3的图象的顶点坐标是( )A、(1,-4) B、(-1,2) C、(1,2) D、(0,3)7. 在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )A、
5. 若方程x2-4x+m=0有两个相等的实数根,则m的值是( ).A、4 B、-4 C、 D、6. 函数y=x2-2x+3的图象的顶点坐标是( )A、(1,-4) B、(-1,2) C、(1,2) D、(0,3)7. 在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )A、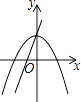 B、
B、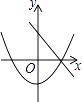 C、
C、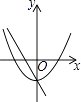 D、
D、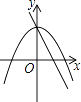 8. 为了改善居民住房条件,我市计划用未来两年的时间,将城镇居民的住房面积由现在的人均约为 提高到 若每年的年增长率相同,则年增长率为A、 B、 C、 D、9. 平面直角坐标系内的点A(-2,3)关于x轴对称点的坐标是( )A、(3,-2) B、(2,-3) C、(-3,-2) D、(-2,-3)10.
8. 为了改善居民住房条件,我市计划用未来两年的时间,将城镇居民的住房面积由现在的人均约为 提高到 若每年的年增长率相同,则年增长率为A、 B、 C、 D、9. 平面直角坐标系内的点A(-2,3)关于x轴对称点的坐标是( )A、(3,-2) B、(2,-3) C、(-3,-2) D、(-2,-3)10.如图,在正方形ABCD中,E为DC边上的点,连接BE,将△BCE绕点C顺时针方向旋转90°得到△DCF,连接EF,若∠BEC=60°,则∠EFD的度数为( )
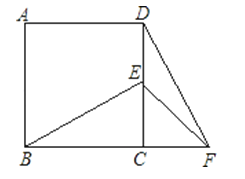 A、10° B、15° C、20° D、25°11. 二次函数y=ax2+bx+c的图象如图所示,若点A(-2.2,y1),B(-3.2,y2)是图象上的两点,则y1与y2的大小关系是( ).
A、10° B、15° C、20° D、25°11. 二次函数y=ax2+bx+c的图象如图所示,若点A(-2.2,y1),B(-3.2,y2)是图象上的两点,则y1与y2的大小关系是( ). A、y1<y2 B、y1=y2 C、y1>y2 D、不能确定12. 把抛物线y=﹣2x2+4x+1的图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系式是( )A、y=﹣2(x﹣1)2+6 B、y=﹣2(x﹣1)2﹣6 C、y=﹣2(x+1)2+6 D、y=﹣2(x+1)2﹣613. 已知二次函数y=ax2+bx+c中x和y的值如下表:( )
A、y1<y2 B、y1=y2 C、y1>y2 D、不能确定12. 把抛物线y=﹣2x2+4x+1的图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系式是( )A、y=﹣2(x﹣1)2+6 B、y=﹣2(x﹣1)2﹣6 C、y=﹣2(x+1)2+6 D、y=﹣2(x+1)2﹣613. 已知二次函数y=ax2+bx+c中x和y的值如下表:( )x
0.10
0.11
0.12
0.13
0.14
y
-5.6
-3.1
-1.5
0.9
1.8
则ax2+bx+c=0的一个根的范围是( )
A、0.10<x<0.11 B、0.11<x<0.12 C、0.12<x<0.13 D、0.13<x<0.1414. 如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )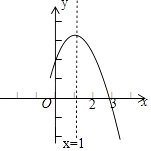 A、①②④ B、①②⑤ C、②③④ D、③④⑤15. 设一元二次方程 的两个实数根为x1 , x2 , 则x1+x1x2+x2等于( ).A、1 B、-1 C、0 D、3
A、①②④ B、①②⑤ C、②③④ D、③④⑤15. 设一元二次方程 的两个实数根为x1 , x2 , 则x1+x1x2+x2等于( ).A、1 B、-1 C、0 D、3二、解答题
-
16. 解方程(1)、x2+x-12=0(2)、x2-3x+2=017. 如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1),(2,1),将△BOC绕点O逆时针旋转90度,得到△B1OC1 , 画出△B1OC1 , 并写出B、C两点的对应点B1、C1的坐标,
 18. 已知关于x的一元二次方程x2+(2m+1)x+m2−2=0.(1)、若该方程有两个实数根,求m的最小整数值;(2)、若方程的两个实数根为x1 , x2 , 且 ,求m的值.19. 空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图,求所利用旧墙AD的长;
18. 已知关于x的一元二次方程x2+(2m+1)x+m2−2=0.(1)、若该方程有两个实数根,求m的最小整数值;(2)、若方程的两个实数根为x1 , x2 , 且 ,求m的值.19. 空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图,求所利用旧墙AD的长; 20. 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按照顺时针方向旋转m度后得到△DEC,点D刚好落在AB边上,求m的值.
20. 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按照顺时针方向旋转m度后得到△DEC,点D刚好落在AB边上,求m的值. 21. 某隧道横断面由抛物线与矩形的三边组成,尺寸如图所示.
21. 某隧道横断面由抛物线与矩形的三边组成,尺寸如图所示. (1)、以隧道横断面抛物线的顶点为原点,以抛物线的对称轴为y轴,建立直角坐标系,求该抛物线对应的函数关系式;(2)、某卡车空车时能通过此隧道,现装载一集装箱箱宽3m,车与箱共高4.5m,此车能否通过隧道?并说明理由22. 某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)、以隧道横断面抛物线的顶点为原点,以抛物线的对称轴为y轴,建立直角坐标系,求该抛物线对应的函数关系式;(2)、某卡车空车时能通过此隧道,现装载一集装箱箱宽3m,车与箱共高4.5m,此车能否通过隧道?并说明理由22. 某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)、求出y与x的函数关系式;
(2)、当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?(3)、设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
23. 某超市为微波炉生产厂代销A型微波炉,售价是每台700元,每台可获利润40%.(1)、超市销售一台A型微波炉可获利多少元?(2)、2019年元旦,超市决定降价销售该微波炉,已知若按原价销售,每天可销售10台,若每台每降价5元,每天可多销1台,同时超市和微波炉生产厂协商,使现有微波炉的成本价,每台减少20元,但生产厂商要求超市尽量增加销售,这样,2019元旦当天超市销售A型微波炉共获利3600元,求超市在元旦当天销售A型微波炉的价格.24. 如图,抛物线y=(x−1)2+n与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,−3),点D与C关于抛物线的对称轴对称. (1)、求抛物线的解析式及点D的坐标;(2)、点P是抛物线上的一点,当△ABP的面积是8,求出点P的坐标;(3)、过直线AD下方的抛物线上一点M作y轴的平行线,与直线AD交于点N,已知M点的横坐标是m,试用含m的式子表示MN的长及△ADM的面积S,并求当MN的长最大时s的值.
(1)、求抛物线的解析式及点D的坐标;(2)、点P是抛物线上的一点,当△ABP的面积是8,求出点P的坐标;(3)、过直线AD下方的抛物线上一点M作y轴的平行线,与直线AD交于点N,已知M点的横坐标是m,试用含m的式子表示MN的长及△ADM的面积S,并求当MN的长最大时s的值.