广东省佛山市顺德区2018-2019学年八年级下学期数学第一次月考试卷

试卷更新日期：2020-01-15 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知 $x > y$ ，那么下列不等式一定成立的是（）

A、 $x - 6 < y - 6$ B、 $- 2 x < - 2 y$ C、 $3 x < 3 y$ D、 $- 2 x + 1 > - 2 y + 1$

查看试题解析
2. 下列说法正确的是（）

A、x=1是不等式-2x＜1的解 B、x=3是不等式-x＜1的解集 C、x＞-2是不等式-2x＜1的解集 D、不等式-x＜1的解集是x＜-1

查看试题解析
3. 不等式－3x+6＞0的正整数解有（）

A、1个 B、2个 C、3个 D、无数多个

查看试题解析
4. 在△ABC中，∠A∶∠B∶∠C=1∶2∶3，最短边BC=4cm，则最长边AB的长是（）

A、5 cm B、6 cm C、 $\sqrt{5}$ cm D、8 cm

查看试题解析
5. 以下各组数为三角形的三条边长，其中是直角三角形的三条边长的是（）

A、2，3，4 B、4，5，6 C、1， $\sqrt{2}$ ， $\sqrt{3}$ D、2， $\sqrt{2}$ ，4

查看试题解析
6. 到三角形三条边距离相等的点是（）

A、三条角平分线的交点 B、三边中线的交点 C、三边上高所在直线的交点 D、三边的垂直平分线的交点

查看试题解析
7. 如图，当 $y > 0$ 时，自变量 $x$ 的范围是（）

A、 $x < - 2$ B、 $x > - 2$ C、 $x > 2$ D、 $x > 0$

查看试题解析
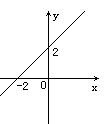8. 已知一次函数y＝kx+b（k、b是常数，且k≠0），x与y的部分对应值如表所示，那么不等式kx+b＜0的解集是（）

x

﹣2

﹣1

0

1

2

3

y

3

2

1

0

﹣1

﹣2

A、x＜0 B、x＞0 C、x＞1 D、x＜2

查看试题解析
9. 若不等式组 ${\begin{array}{l} x \leq m \\ x > 3 \end{array}$ 无解，则 $m$ 的取值范围是（）

A、 $m$ ＜3 B、 $m$ ＞3 C、 $m$ ≤3 D、 $m$ ≥3

查看试题解析
10. 等腰三角形一腰上的高等于这腰的一半，则这个等腰三角形的顶角等于（）

A、30° B、60° C、30°或150° D、60°或120°

查看试题解析

二、填空题

11. 当x时，代数式2x－3的值是正数．

查看试题解析
12. 若不等式（2k+1）x＜2k+1的解集是x＞1，则k的范围是．

查看试题解析
13. 如图，在△ABC中，∠C＝90°，∠B＝30°，AD平分∠CAB，交BC于点D，若CD＝1，则BD＝．

查看试题解析
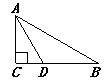14.
如图，△ABC中，D是BC上一点，AC=AD=DB，∠BAC=102°，则∠ADC=度．

查看试题解析
15. 如图，已知△ABC的周长是20cm，BO，CO分别平分∠ABC和∠ACB，OD⊥BC于点D，且OD=3cm，则△ABC的面积是 $c m^{2}$

查看试题解析
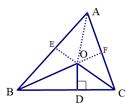16. 如图，已知：∠MON=30°，点A₁、A₂、A₃ 在射线ON上，点B₁、B₂、B₃…在射线OM上，△A₁B₁A₂、△A₂B₂A₃、△A₃B₃A₄…均为等边三角形，若OA₁=a，则△A₆B₆A₇的边长为．

查看试题解析

三、解答题

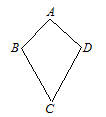
17. 解不等式 $\frac{x - 5}{5}$ +4＜ $\frac{x + 4}{2}$ ，并把解集在数轴表示出来。

查看试题解析
18. 解不等式组 ${\begin{array}{l} 3 （ x + 3 ） > 4 x + 7 \\ x - 1 \geq \frac{x - 7}{3} \end{array}$ 并写出它的所有整数解．

查看试题解析
19. 如图，在四边形ABCD中，AB＝AD ， ∠ABC＝∠ADC ．求证：BC＝DC ．

查看试题解析
20. 如图，AD为△ABC的高，E为AC上一点，BE交AD于F，且有BF=AC， FD=CD。

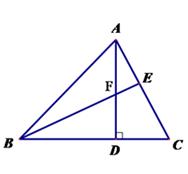
求证：

(1)、Rt△BDF≌Rt△ADC

(2)、BE⊥AC

查看试题解析
21. 如图，在△ABC中，∠C=90°，∠CAB=60°，

(1)、作AB边上的中垂线交BC边于点E，交AB边于点D（保留作图痕迹，不写作法和证明）

(2)、连接AE，若CE=4，求AE的长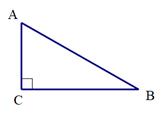

查看试题解析

22. 2018年4月23日，第23个世界读书日．为了推进中华传统文化教育，营造浓郁的读书氛围，我区某学校举办了“让读书成为习惯，让书香飘满校园”主题活动，为此特为每个班级订购了一批新的图书．初二年级两个班订购图书情况如下表：

	老舍文集（套）	四大名著（套）	总费用（元）
初二（1）班	4	2	480
初二（2）班	2	3	520

(1)、求老舍文集和四大名著每套各是多少元；

(2)、学校准备再购买老舍文集和四大名著共10套，总费用不超过700元，问学校有哪几种购买方案．

查看试题解析

23. 如图所示，根据图中的信息.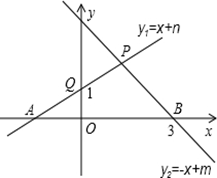

(1)、求m、n的值，

(2)、求出P点的坐标，

(3)、当 $x$ 为何值时， $y_{1} > y_{2}$

查看试题解析
24. 如图，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形．BE交AC于F，AD交CE于H，

(1)、求证：△BCE≌△ACD；

(2)、求证：FC=HC

(3)、求证：FH∥BD．

查看试题解析
25. 在△ABC中，AB=AC，D是线段BC的延长线上一点，以AD为一边在AD的右侧作△ADE，使AE=AD，∠DAE=∠BAC，连接CE．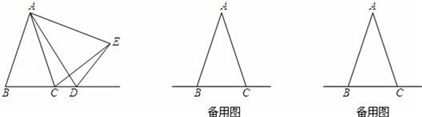

(1)、如图1，点D在线段BC的延长线上移动，若∠BAC=30°，则∠DCE= ．

(2)、设∠BAC=α，∠DCE=β：
①如图1，当点D在线段BC的延长线上移动时，α与β之间有什么数量关系？请说明理由；

②当点D在直线BC上（不与B、C重合）移动时，α与β之间有什么数量关系？请直接写出你的结论．

查看试题解析

x	﹣2	﹣1	0	1	2	3
y	3	2	1	0	﹣1	﹣2