湖北省黄石市2020届九年级上学期数学期中考试试卷

试卷更新日期：2020-01-15 类型：期中考试

进入出卷网下载

一、单选题

1. 观察下列图形，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 将一元二次方程x²＋1＝3x化成一般形式后，二次项系数和一次项系数分别为（）

A、1，－3. B、1，3. C、1，0. D、x² ，－3x.

查看试题解析
3. 抛物线y=（m﹣1）x²﹣mx﹣m²+1的图象过原点，则m的值为（　　）

A、±1 B、0 C、1 D、-1

查看试题解析
4. 已知关于x的方程(a﹣3)x^|a^﹣^1|+x﹣1＝0是一元二次方程，则a的值是（）

A、﹣1 B、2 C、﹣1或3 D、3

查看试题解析
5. 二次函数y＝ax²+bx+c的图象如图所示，那么一次函数y＝ax﹣bc的图象大致是（　　）

A、 B、 C、 D、

查看试题解析
6. 如图所示，将一个含30°角的直角三角板ABC绕点A逆时针旋转，点B的对应点是点B′，若点B′、A、C在同一条直线上，则三角板ABC旋转的度数是（　　）

A、60° B、90° C、120° D、150°

查看试题解析
7. 如图，BC是 $⊙ O$ 的直径，A，D是 $⊙ O$ 上的两点，连接AB，AD，BD，若 $∠ A D B = 70^{°}$ ，则 $∠ A B C$ 的度数是（）

A、 $20^{°}$ B、 $70^{°}$ C、 $30^{°}$ D、 $90^{°}$

查看试题解析
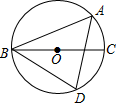8. 《九章算术》是我国古代著名数学著作，书中记载：“今有圆材，埋在壁中，不知大小以锯锯之，深一寸，锯道长一尺，问径几何？”用数学语言可表述为：“如图， $C D$ 为 $⊙ O$ 的直径，弦 $A B ⊥ D C$ 于 $E$ ， $E D = 1$ 寸， $A B = 10$ 寸，求直径 $C D$ 的长.”则 $C D =$ （）

A、 $13$ 寸 B、 $20$ 寸 C、 $26$ 寸 D、 $28$ 寸

查看试题解析
9. 已知二次函数y＝ax²+bx+c(a≠0)的图象如图所示，给出以下结论：①a+b+c＜0；②a﹣b+c＜0；③b+2a＜0；④abc＞0.其中所有正确结论的序号是（）

A、③④ B、②③ C、①④ D、①②③

查看试题解析
10. 将二次函数y＝x²﹣5x﹣6在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新图象，若直线y＝2x+b与这个新图象有3个公共点，则b的值为（）

A、﹣ $\frac{73}{4}$ 或﹣12 B、﹣ $\frac{73}{4}$ 或2 C、﹣12或2 D、﹣ $\frac{69}{4}$ 或﹣12

查看试题解析

二、填空题

11. 方程x²+x=0的解是　 .

查看试题解析
12. 关于x的一元二次方程（m﹣1）x²+2x﹣1＝0没有实数根，则m的取值范围是.

查看试题解析
13. 抛物线y＝（x﹣2）²的对称轴是.

查看试题解析
14. 如图，A，B，C，D是⊙O上的四点，且点B是 $\overset{⌢}{A C}$ 的中点，BD交OC于点E，∠AOC＝100°，∠OCD＝35°，那么∠OED＝.

查看试题解析
15. 若点 $M (3, a - 2)$ ， $N (b, a)$ 关于 $x$ 轴对称，则 $a + b =$ ..

查看试题解析
16. 已知二次函数y＝﹣3x²+（m﹣1）x+1，当x＞ $\frac{m + 1}{2}$ 时，y随x的增大而减小，则m的取值范围是.

查看试题解析

三、解答题

17. 解方程：

(1)、（2x﹣1）²＝（x﹣3）²；

(2)、x²﹣2 $\sqrt{2}$ x﹣1＝0

查看试题解析
18. 先化简，再求值： $(m + \frac{4 m + 4}{m}) \div \frac{m + 2}{m^{2}}$ ，其中m是方程 $2 x^{2} + 4 x - 1 = 0$ 的根.

查看试题解析
19. 已知抛物线y＝﹣x²+4x+5

(1)、用配方法将y＝﹣x²+4x+5化成y＝a（x﹣h）²+k的形式；

(2)、写出抛物线的开口方向、对称轴和顶点坐标.

查看试题解析
20. 随着粤港澳大湾区建设的加速推进，广东省正加速布局以5G等为代表的战略性新兴产业，据统计，目前广东5G基站的数量约1.5万座，计划到2020年底，全省5G基站数是目前的4倍，到2022年底，全省5G基站数量将达到17.34万座。

(1)、计划到2020年底，全省5G基站的数量是多少万座？；

(2)、按照计划，求2020年底到2022年底，全省5G基站数量的年平均增长率。

查看试题解析
21. 已知关于x的一元二次方程x²﹣2（a﹣1）x+a²﹣a﹣2＝0有两个不相等的实数根x₁ ， x₂.

(1)、若a为正整数，求a的值；

(2)、若x₁ ， x₂满足x₁²+x₂²﹣x₁x₂＝16，求a的值.

查看试题解析
22. 已知AB是⊙O的直径，弦CD⊥AB于点E.

(1)、如图①，若CD＝8，BE＝2，求⊙O的半径；

(2)、如图②，点G是 $\overset{⌢}{A C}$ 上一点，AG的延长线与DC的延长线交于点F，求证：∠AGD＝∠FGC.

查看试题解析
23. 某服装超市购进单价为30元的童装若干件，物价部门规定其销售单价不低于每件30元，不高于每件60元.销售一段时间后发现：当销售单价为60元时，平均每月销售量为80件，而当销售单价每降低10元时，平均每月能多售出20件.同时，在销售过程中，每月还要支付其他费用450元.设销售单价为x元，平均月销售量为y件.

(1)、求出y与x的函数关系式，并写出自变量x的取值范围.

(2)、当销售单价为多少元时，销售这种童装每月可获利1800元？

(3)、当销售单价为多少元时，销售这种童装每月获得利润最大？最大利润是多少？

查看试题解析
24.

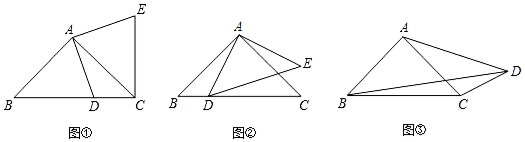(1)、问题：如图①，在Rt△ABC中，AB＝AC，D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC，则线段BC，DC，EC之间满足的等量关系式为；

(2)、探索：如图②，在Rt△ABC与Rt△ADE中，AB＝AC，AD＝AE，将△ADE绕点A旋转，使点D落在BC边上，试探索线段AD，BD，CD之间满足的等量关系，并证明你的结论；

(3)、应用：如图③，在四边形ABCD中，∠ABC＝∠ACB＝∠ADC＝45°.若BD＝9，CD＝3，求AD的长.

查看试题解析
25.
如图，抛物线 $y = \frac{1}{2} x^{2} + b x - 2$ 与x轴交于A、B两点，与y轴交于C点，且A（﹣1，0）．

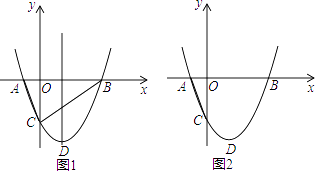(1)、求抛物线的解析式及顶点D的坐标；

(2)、判断△ABC的形状，证明你的结论；

(3)、点M是抛物线对称轴上的一个动点，当CM+AM的值最小时，求M的坐标；

(4)、在线段BC下方的抛物线上有一动点P，求△PBC面积的最大值．

查看试题解析