河南省洛阳市偃师市2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-01-15 类型:期中考试
一、单选题
-
1. 已知ab<0,则 化简后为( )A、 B、 C、 D、2. 下列根式是最简二次根式的是( )A、 B、 C、 D、3. 如果a是一元二次方程x2﹣3x﹣5=0的一个根,那么代数式8﹣a2+3a的值为( )A、1 B、2 C、3 D、44. 如果一元二次方程 满足 ,那么我们称这个方程为“阿凡达”方程,已知 是“阿凡达”方程,且有两个相等的实数根,则下列结论正确的是( )
A、 B、 C、 D、5. 已知2x=3y,那么下列结论中不正确的是( )A、 B、 C、 D、6. 如图,已知△ABC中,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,若AB=7,MN=3,则AC的长为( )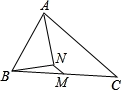 A、14 B、13 C、12 D、117. 如图,P是Rt△ABC的斜边BC上异于端点B,C的点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )
A、14 B、13 C、12 D、117. 如图,P是Rt△ABC的斜边BC上异于端点B,C的点,过P点作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )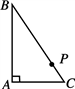 A、1条 B、2条 C、3条 D、4条8. 如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知sinα= ,则小车上升的高度是( )
A、1条 B、2条 C、3条 D、4条8. 如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知sinα= ,则小车上升的高度是( )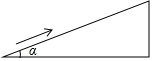 A、5米 B、6米 C、6.5米 D、7米9. 如图所示的网格是正方形网格,点A,B,C都在格点上,则tan∠BAC的值为( )
A、5米 B、6米 C、6.5米 D、7米9. 如图所示的网格是正方形网格,点A,B,C都在格点上,则tan∠BAC的值为( ) A、2 B、 C、 D、10. 如图,将 绕点 旋转180°得到 ,设点 的坐标为 ,则点 的坐标为( )
A、2 B、 C、 D、10. 如图,将 绕点 旋转180°得到 ,设点 的坐标为 ,则点 的坐标为( )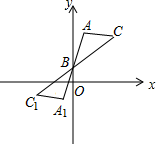 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 当x时,在 实数范围内有意义.12. 已知实数a、b、c在数轴上的位置如图所示,化简 ﹣|a﹣c|+ ﹣|﹣b|=.
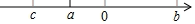 13. 若关于x的方程(m﹣2)x2+ +1=0是一元二次方程,则m的取值范围是.14. 如图,已知舞台AB长10米,如果报幕员从点A出发站到舞台的黄金分割点P处,且 ,那么报幕员应走米报幕;
13. 若关于x的方程(m﹣2)x2+ +1=0是一元二次方程,则m的取值范围是.14. 如图,已知舞台AB长10米,如果报幕员从点A出发站到舞台的黄金分割点P处,且 ,那么报幕员应走米报幕;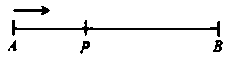 15. 如图,已知sinO= ,OA=6,点P是射线ON上一动点,当△AOP为直角三角形时,则AP=.
15. 如图,已知sinO= ,OA=6,点P是射线ON上一动点,当△AOP为直角三角形时,则AP=.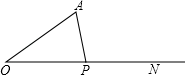
三、解答题
-
16. 计算:(1)、 .(2)、2|1﹣sin60°|+ .17. 解方程.(1)、x2﹣2x﹣2=0.(2)、5x+2=3x2.(3)、5(x﹣3)2=x2﹣9.(4)、(y﹣3)(y﹣1)=8.18. 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,该店采取了降价措施,在每件盈利不小于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件(1)、若降价5元,求平均每天的销售量以及每天的盈利;(2)、当每件商品降价多少元时,该商店每天的盈利为1200元?19. 2019年4月23日是中国人民解放军海军成立70周年纪念日,届时将在青岛举行盛大的多国海军庆祝活动.为此我国海军进行了多次军事演习.如图,在某次军事演习时,舰艇A发现在他北偏东22°方向上有不明敌舰在指挥中心O附近徘徊,快速报告给指挥中心,此时在舰艇A正西方向50海里处的舰艇B接到返回指挥中心的行动指令,舰艇B迅速赶往在他北偏东60°方向的指挥中心处,舰艇B的速度是80海里/小时,请根据以上信息,求舰艇B到达指挥中心O的时间.(结果精确到0.1小时,参考数据:(sin22°≈0.37,cos22°≈0.93,tan22°≈0.40, =1.73)
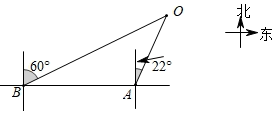 20. 如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y= (x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
20. 如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y= (x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.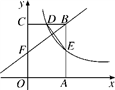 (1)、求点D的坐标;(2)、点F是OC边上一点,若△FBC和△DEB相似,求点F的坐标.21. 如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角为45°,沿斜坡走3 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
(1)、求点D的坐标;(2)、点F是OC边上一点,若△FBC和△DEB相似,求点F的坐标.21. 如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角为45°,沿斜坡走3 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.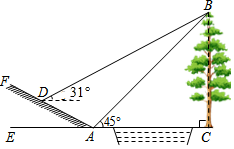 (1)、求小明从点A到点D的过程中,他上升的高度;(2)、大树BC的高度约为多少米?(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)22. 在△ABC中,D、E分别是AB,AC的中点,作∠B的角平分线
(1)、求小明从点A到点D的过程中,他上升的高度;(2)、大树BC的高度约为多少米?(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)22. 在△ABC中,D、E分别是AB,AC的中点,作∠B的角平分线
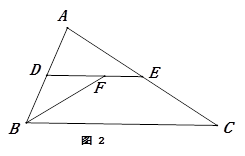 (1)、如图1,若∠B的平分线恰好经过点E,猜想△ABC是怎样的特殊三角形,并说明理由;(2)、如图2,若∠B的平分线交线段DE于点F,已知AB=8,BC=10,求EF的长度;(3)、若∠B的平分线交直线DE于点F,直接写出AB、BC、EF三者之间的数量关系。23. 在∠ABC中,∠ABC=90°,tan∠BAC= .
(1)、如图1,若∠B的平分线恰好经过点E,猜想△ABC是怎样的特殊三角形,并说明理由;(2)、如图2,若∠B的平分线交线段DE于点F,已知AB=8,BC=10,求EF的长度;(3)、若∠B的平分线交直线DE于点F,直接写出AB、BC、EF三者之间的数量关系。23. 在∠ABC中,∠ABC=90°,tan∠BAC= .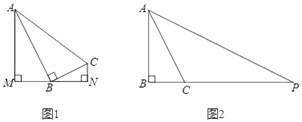 (1)、如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,若点B恰好是线段MN的中点,求tan∠BAM的值;(2)、如图2,P是边BC延长线上一点,∠APB=∠BAC,求tan∠PAC的值.
(1)、如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,若点B恰好是线段MN的中点,求tan∠BAM的值;(2)、如图2,P是边BC延长线上一点,∠APB=∠BAC,求tan∠PAC的值.