重庆市九龙坡区十校2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2020-01-15 类型:期中考试
一、单选题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下列长度的线段为边,可以作一个三角形的是A、6cm,16cm,21cm B、8cm,16cm,30cm C、6cm,16cm,24cm D、8cm,16cm,24cm3. 下列图形中具有稳定性的是( )A、正方形 B、长方形 C、等腰三角形 D、平行四边形4. 下列各组图形中,AD是 的高的图形是( )A、
2. 以下列长度的线段为边,可以作一个三角形的是A、6cm,16cm,21cm B、8cm,16cm,30cm C、6cm,16cm,24cm D、8cm,16cm,24cm3. 下列图形中具有稳定性的是( )A、正方形 B、长方形 C、等腰三角形 D、平行四边形4. 下列各组图形中,AD是 的高的图形是( )A、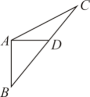
B、
B、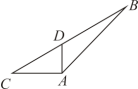
C、
C、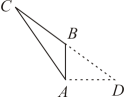
D、
D、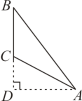
5. 如果等腰三角形的一个角是80°,那么它的底角是( )A、80°或50° B、50°或20° C、80°或20° D、50°6. 下列说法正确的是( )A、两个等边三角形一定全等 B、形状相同的两个三角形全等 C、面积相等的两个三角形全等 D、全等三角形的面积一定相等7. 如图 ,若 , ,则 的度数为( )
5. 如果等腰三角形的一个角是80°,那么它的底角是( )A、80°或50° B、50°或20° C、80°或20° D、50°6. 下列说法正确的是( )A、两个等边三角形一定全等 B、形状相同的两个三角形全等 C、面积相等的两个三角形全等 D、全等三角形的面积一定相等7. 如图 ,若 , ,则 的度数为( )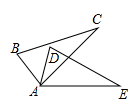 A、 B、 C、 D、8. 已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则a+b的值为( )A、9 B、7 C、-1 D、-29. 如图,在△ABC中∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE+DE等于( )
A、 B、 C、 D、8. 已知点P1(a-1,5)和P2(2,b-1)关于x轴对称,则a+b的值为( )A、9 B、7 C、-1 D、-29. 如图,在△ABC中∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE+DE等于( )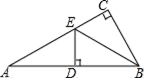 A、3cm B、4cm C、5cm D、6cm10. 一个正方形和两个等边三角形的位置如图所示,则∠1+∠2+∠3的度数为( )
A、3cm B、4cm C、5cm D、6cm10. 一个正方形和两个等边三角形的位置如图所示,则∠1+∠2+∠3的度数为( )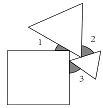 A、1500 B、1200 C、900 D、180011. 如图,△ABC的中线BD、CE相交于点O,OF⊥BC,垂足为F,四边形ADOE的面积是6,且BC=6,则OF的长是( )
A、1500 B、1200 C、900 D、180011. 如图,△ABC的中线BD、CE相交于点O,OF⊥BC,垂足为F,四边形ADOE的面积是6,且BC=6,则OF的长是( )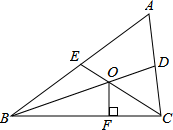 A、1.5 B、2 C、2.5 D、312. 如图:已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC边上的中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:①AE=CF;②EF=AP;③2S四边形AEPF=S△ABC;④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合)有BE+CF=EF;上述结论中始终正确的序号有( )个
A、1.5 B、2 C、2.5 D、312. 如图:已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC边上的中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:①AE=CF;②EF=AP;③2S四边形AEPF=S△ABC;④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合)有BE+CF=EF;上述结论中始终正确的序号有( )个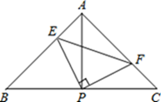 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
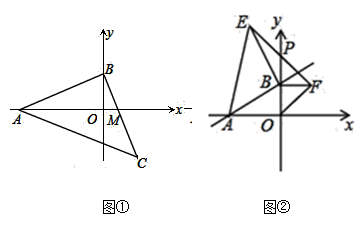
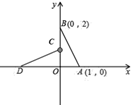
13. 已知正n边形的一个外角是45°,则n=14. 如图,在平面直角坐标系中,DC=AB,OD=OB,则点C的坐标是.
 15. 等腰三角形的底角为15°,腰长为20cm,则此三角形的面积为。16. 如图,CE平分∠ACB,且CE⊥BD,DA=DB,又知AC=18,△CDB的周长为28,那么BE的长为
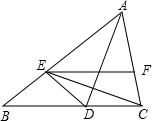
15. 等腰三角形的底角为15°,腰长为20cm,则此三角形的面积为。16. 如图,CE平分∠ACB,且CE⊥BD,DA=DB,又知AC=18,△CDB的周长为28,那么BE的长为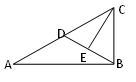 17. 如图,点P在AC上,点Q在AB上,BE平分∠ABP,交AC于E,CF平分∠ACQ,交AB于F,BE、CF相交于G,CQ、BP相交于D,若∠BDC=140°,∠BGC=110°,则∠A的度数为
17. 如图,点P在AC上,点Q在AB上,BE平分∠ABP,交AC于E,CF平分∠ACQ,交AB于F,BE、CF相交于G,CQ、BP相交于D,若∠BDC=140°,∠BGC=110°,则∠A的度数为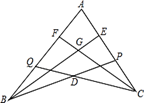 18. 四边形ABCD中,∠B=∠D=90°,∠C=72°,在BC、CD上分别找一点M、N,使△AMN的周长最小时,∠AMN+∠ANM的度数为
18. 四边形ABCD中,∠B=∠D=90°,∠C=72°,在BC、CD上分别找一点M、N,使△AMN的周长最小时,∠AMN+∠ANM的度数为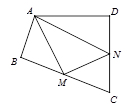
三、解答题
-
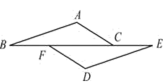
19. 如图,点B,F,C,E在同一直线上,AB=DE,BF=CE,AB∥DE,求证:AC=DF.
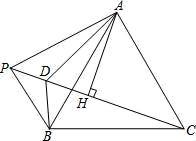
 20. 某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行7海里后,在B处测得小岛P的方位是北偏东60°,求:
20. 某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行7海里后,在B处测得小岛P的方位是北偏东60°,求: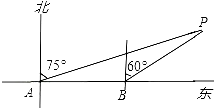 (1)、此时轮船与小岛P的距离BP是多少海里;(2)、小岛点P方圆3海里内有暗礁,如果轮船继续向东行使,请问轮船有没有触焦的危险?请说明理由.21. 如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=80°,∠C=54°,求∠DAC、∠BOA的度数.
(1)、此时轮船与小岛P的距离BP是多少海里;(2)、小岛点P方圆3海里内有暗礁,如果轮船继续向东行使,请问轮船有没有触焦的危险?请说明理由.21. 如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=80°,∠C=54°,求∠DAC、∠BOA的度数.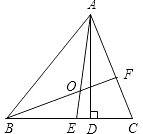 22. 如图,△ABC是等边三角形,CD⊥AB于点D,∠AEB=90°,CD=AE.
22. 如图,△ABC是等边三角形,CD⊥AB于点D,∠AEB=90°,CD=AE.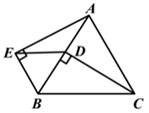
求证:
(1)、△BCD≌△BAE;(2)、△EBD是等边三角形.23. 如图,AD是∠BAC的平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,试说明:EC平分∠DEF.