江苏省盐城市东台市第四联盟2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期：2020-01-15 类型：期中考试
一、单选题
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 如图，△ABC≌△ADE，∠B=20°，∠E=110°，则∠EAD的度数为（ ）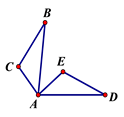
A、80° B、70° C、50° D、130°3. 已知：如图，∠1＝∠2，则不一定能使△ABD≌△ACD的条件是 （ ）
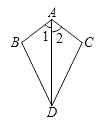A、AB＝AC B、BD＝CD C、∠B＝∠C D、∠BDA＝∠CDA4. 下列长度的三条线段能组成直角三角形的是（ ）A、2cm，3cm，4cm B、3cm，4cm，5cm C、4cm，5cm，6cm D、5cm，6cm，7cm5. 到三角形三条边距离相等的点是（ ）A、三条角平分线的交点 B、三边中线的交点 C、三边上高所在直线的交点 D、三边的垂直平分线的交点6. 如图，AC＝AD，BC＝BD，则有（ ）
A、AB垂直平分CD B、CD垂直平分AB C、AB与CD互相垂直平分 D、CD平分∠ACB7. 如图所示，是用直尺和圆规作一个角等于已知角的示意图，则说明 的依据是（ ）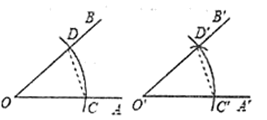
A、 B、 C、 D、8. 如图的2×4的正方形网格中，△ABC的顶点都在小正方形的格点上，这样的三角形称为格点三角形，在网格中与△ABC成轴对称的格点三角形一共有（ ）
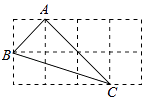A、2个 B、3个 C、4个 D、5个二、填空题
-
9. 写出一个你熟悉的轴对称图形的名称： ．10. 4的算术平方根是 ， 9的平方根是 ， ﹣27的立方根是 ．11. 若等腰三角形的一个底角为40°，则它的顶角为度.12. 若一正数的两个平方根分别是2a﹣1与a+4，则a等于.13. 已知等腰三角形其中两边长为3cm和7cm，则它的周长为cm.14. 甲、乙两人同时从同一地点出发，甲往东走了8km，乙往南走了6km，这时两人相距km.15. 如图，在△ABC中，∠C=90°，AD平分∠CAB，CD=5 cm，那么D点到直线AB的距离是cm.
16. 如图，△ABC中，边AB的垂直平分线DE交边AB于D，交边BC于E，若BC=8，AC=6，则△ACE的周长为.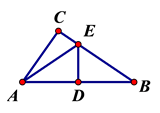
17. 如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、D的边长分别是2，3，1，2，则最大正方形E的面积是.
18. 如图，在△ABC 中，AC＝BC，∠ACB＝90°，点 D 在 BC 上，BD＝3，DC＝1，点 P 是 AB 上的动点，则 PC+PD 的最小值为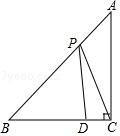
三、解答题
-
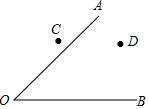
19. 求出下列x的值(1)、x2=4(2)、2(x+1)3= -1620. 尺规作图：校园有两条路OA、OB，在交叉路口附近有两块宣传牌C、D，学校准备在这里安装一盏路灯，要求灯柱的位置P离两块宣传牌一样远，并且到两条路的距离也一样远，请你帮助画出灯柱的位置P.（不写画图过程，保留作图痕迹）
21. 已知：如图，AD，BC相交于点O，OA=OD，AB∥CD.求证：AB=CD.
22. 如图，在△ABC中，CD⊥AB于D，AD=9，BD=16，CD=12.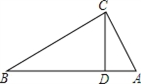
(1)、求△ABC的周长；(2)、△ABC是直角三角形吗？请说明理由.23. 如图，在△ABC中，∠ABC与∠ACB的平分线交于点O，过点O作DE∥BC，分别交AB、AC于点D、E.
(1)、△BDO是等腰三角形吗？请说明理由.(2)、若AB=10，AC=6，求△ADE的周长.24. 已知：如图∠ABC=∠ADC=90°，M，N分别是AC、BD的中点.
(1)、试判断△BMD的形状，并说明理由.(2)、求证： MN⊥BD.25. 如图，在等腰直角三角形ABC中，∠ABC=90°，D为AC边中点，过D点作DE⊥DF，分别交边AB、BC于点E、F，连接BD.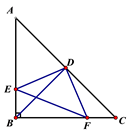
(1)、求证：△BDE≌△CDF.(2)、若AE=4，FC=3，求EF长.26.(1)、如图，在△ABC中，∠ACB=90° ， AC=12，BC=5，AM=AC，BN=BC，求MN的长.
(2)、如图，在△ABC中，∠ACB=90°，AM=AC，BN=BC当∠A=30°时，求∠MCN的度数。
当∠A的度数变化时，∠MCN的度数是否变化，如有变化，请说明理由；如不变，求∠MCN的度数.
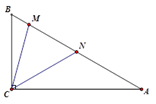(3)、如图，在△ABC中，∠ACB=90，AC=BC，点M、N在边AB上，且∠MCN=45°，试猜想线段AN、BM、MN之间的数学关系，直接写出你的结论（不要求证明）.