江苏省盐城市东台市第二联盟2019-2020学年八年级上学期数学期中考试试卷

试卷更新日期：2020-01-15 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 下列四个图案，其中是轴对称图形的是（　　）
    A、 B、 C、 D、

    查看试题解析

  • 2. 在﹣0.101001， 7 ， 14 ，0，﹣ π2 ，0.010010001……中，无理数的个数为 （ ）
    A、1 B、2 C、3 D、4

    查看试题解析

  • 3. 下列给出的三条线段的长，能组成直角三角形的是（   ）
    A、1 、 2 、3 B、2 、 3、 4 C、5、 7  、 9 D、5、 12、 13

    查看试题解析

  • 4. 如图，△ABC≌△DEF，点A与D，B与E分别是对应顶点，且测得BC=5cm，BF=7cm，则EC长为（　 ）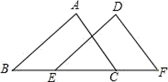   

    A、2cm B、3cm C、4cm D、5cm

    查看试题解析

  • 5. 如图，△ABC≌△ADE，AB=AD，AC=AE，∠B=20°，∠E=120°，∠EAB=15°，则   ∠BAD的度数为（　　）

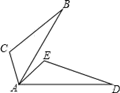    A、85° B、75° C、65° D、55°

    查看试题解析

  • 6. 已知：如图，∠1＝∠2，则不一定能使△ABD≌△ACD的条件是 （     ）

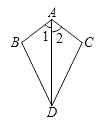    A、AB＝AC B、BD＝CD C、∠B＝∠C D、∠BDA＝∠CDA

    查看试题解析

  • 7. 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7米，顶端距离地面2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2米，那么小巷的宽度为（ ）

    A、0.7米 B、1.5米 C、2.2米 D、2.4米

    查看试题解析

  • 8.

    如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1 ， P2 ， P3 ， P4四个点中找出符合条件的点P，则点P有（　　）

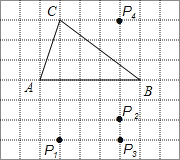    A、1个 B、2个 C、3个 D、4个

    查看试题解析

二、填空题

  • 9. 16的算术平方根是 ，5﹣2的相反数是 　，-83的绝对值是 ．

    查看试题解析

  • 10. 若一正数的两个平方根分别是2a﹣1与2a+5，则这个正数等于.

    查看试题解析

  • 11. 已知△ABC≌△DEF，若∠B=40°，∠D=60°，则∠F=°.

    查看试题解析

  • 12. 若 ΔABC 的三边长分别是6、8、10，则最长边上的中线长为.

    查看试题解析

  • 13. 如图，在△ABC中，AB=AC，BC=8，AD⊥BC于D，则BD=.

    查看试题解析

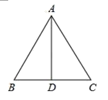  • 14. 已知，如图：∠ABC=∠DEF，AB=DE，要说明△ABC≌△DEF，若以“ASA”为依据，还要添加的条件为.

    查看试题解析

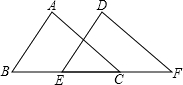  • 15. 如图，已知△ABC的周长是22，OB和OC分别平分∠ABC和∠ACB，OD⊥BC于点D，且OD=3，则△ABC的面积是.

    查看试题解析

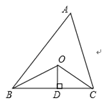  • 16. 如图，四边形ABCD中，∠BAD=110°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小，此时∠MAN的度数为°.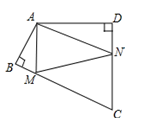

    查看试题解析

三、解答题

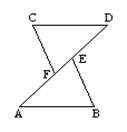
  • 17. 解方程和计算
    (1)、2x2=50
    (2)、16−(−2)2+(2−3)0

    查看试题解析

  • 18. 已知如图：点A，F，E，D在同一条直线上， AB=CD ， BE=CF ， AF=DE.求证：△ABE≌△DCF

    查看试题解析

  • 19. 作图题：（要求保留作图痕迹，不写做法）

    如图，已知∠AOB与点M、N.

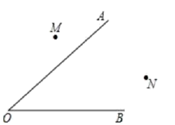
    求作：点P，使点P到OA、OB的距离相等，且到点M与点N的距离也相等.(不写作法与证明，保留作图痕迹)

    查看试题解析

  • 20. 如图：在△ABC中，∠C=90°，AD平分∠BAC，DE⊥AB于点E，点F在AC上，且BD=DF，

    (1)、求证：CF=EB；
    (2)、请你判断AE、AF与BE之间的数量关系，并说明理由.

    查看试题解析

  • 21. 如图，在 △ABC 中， AC<AB<BC .
    (1)、已知线段AB的垂直平分线与BC边交于点P，连结AP

    求证： ∠APC=2∠B ；

    (2)、以点B为圆心，线段AB的长为半径画弧，与BC边交于点Q，连结AQ，若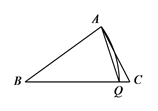 ∠AQC=3∠B ，求 ∠B 的度数.

    查看试题解析

  • 22. 如图，折叠长方形一边AD，点D落在BC边的点F处，BC=10cm，AB=8cm.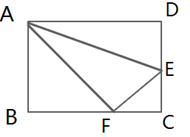

    求：

    (1)、FC的长；
    (2)、EF的长.

    查看试题解析

  • 23. 如图，在等腰直角三角形ABC中，∠ABC=90°，D为AC边中点，过D点作DE⊥DF，交AB于E，交BC于F.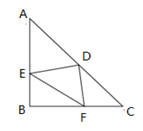

    (1)、求证：DE=DF.
    (2)、若AE=8，FC=6，求EF长.

    查看试题解析

  • 24. 如图，铁路上A，B两点相距25 km，C，D为两村庄，DA⊥AB于点A，CB⊥AB于点B，已知DA＝15 km，CB＝10 km，现在要在铁路AB上建一个土特产品收购站E，使得C，D两村到E站的距离相等，则E站应建在离A站多少km处？

    查看试题解析

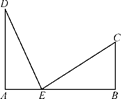  • 25. 如图，在长度为1个单位长度的小正方形组成的大正方形中，点A、B、C在小正方形的顶点上.

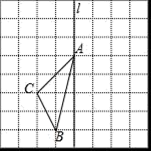    (1)、在图中画出与△ABC关于直线l成轴对称的△AB′C′；
    (2)、△ABC的面积为；
    (3)、△ABC的周长为；(保留根号)
    (4)、在直线l上找一点P，使PB+PC的长最短.(保留痕迹)

    查看试题解析

  • 26. 旋转变换是解决数学问题中一种重要的思想方法，通过旋转变换可以将分散的条件集中到一起，从而方便解决问题.

    已知，△ABC中，AB＝AC，∠BAC＝α，点D、E在边BC上，且∠DAE＝ 12 α.

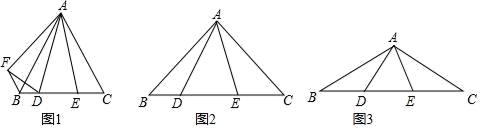    (1)、如图1，当α＝60°时，将△AEC绕点A顺时针旋转60°到△AFB的位置，连接DF，

    ①求∠DAF的度数；

    ②求证：△ADE≌△ADF；

    (2)、如图2，当α＝90°时，猜想BD、DE、CE的数量关系，并说明理由；
    (3)、如图3，当α＝120°，BD＝4，CE＝5时，请直接写出DE的长为.

    查看试题解析