河南省驻马店市确山县2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2020-01-15 类型:期中考试
一、单选题
-
1. 下列大学的校徽图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知三角形的两边分别为1和4,第三边长为整数 ,则该三角形的周长为( )A、7 B、8 C、9 D、103. 将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )。
2. 已知三角形的两边分别为1和4,第三边长为整数 ,则该三角形的周长为( )A、7 B、8 C、9 D、103. 将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )。 A、45° B、60° C、75° D、85°4. 如图,点F,C在BE上,△ABC≌△DEF,AB和DE,AC和DF是对应边,AC,DF交于点M,则∠AMF等于( )
A、45° B、60° C、75° D、85°4. 如图,点F,C在BE上,△ABC≌△DEF,AB和DE,AC和DF是对应边,AC,DF交于点M,则∠AMF等于( )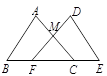 A、2∠B B、2∠ACB C、∠A+∠D D、∠B+∠ACB5. 如果一个三角形的外角平分线与这个三角形的一边平行,则这个三角形一定是( )A、等腰三角形 B、等边三角形 C、等腰直角三角形 D、无法确定6.
A、2∠B B、2∠ACB C、∠A+∠D D、∠B+∠ACB5. 如果一个三角形的外角平分线与这个三角形的一边平行,则这个三角形一定是( )A、等腰三角形 B、等边三角形 C、等腰直角三角形 D、无法确定6.如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
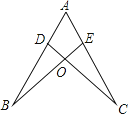 A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD7. 如果多边形的内角和是外角和的k倍,那么这个多边形的边数是A、k B、 C、 D、8. 如图,在 中, 分别是 的中点,若 ,则 ( )
A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD7. 如果多边形的内角和是外角和的k倍,那么这个多边形的边数是A、k B、 C、 D、8. 如图,在 中, 分别是 的中点,若 ,则 ( )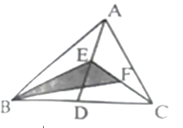 A、 B、 C、 D、9. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画圆弧,分别交AB、AC于点D、E,再分别以点D、E为圆心,大于 DE长为半径画圆弧,两弧交于点F,作射线AF交边BC于点G.若CG=3,AB=10,则△ABG的面积是( )
A、 B、 C、 D、9. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画圆弧,分别交AB、AC于点D、E,再分别以点D、E为圆心,大于 DE长为半径画圆弧,两弧交于点F,作射线AF交边BC于点G.若CG=3,AB=10,则△ABG的面积是( )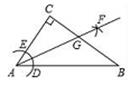 A、3 B、10 C、15 D、3010. 如图,在 中, , , ,则 ( )
A、3 B、10 C、15 D、3010. 如图,在 中, , , ,则 ( )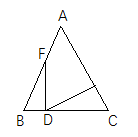 A、50° B、55° C、60° D、65°
A、50° B、55° C、60° D、65°二、填空题
-
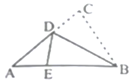
11. 一个等腰三角形的一边长是2,一个外角是120°,则它的周长是.12. 如图,在三角形纸片中, ,沿过点 的直线折叠这个三角形,使点 落在 边上的点 处,折痕为 ,则 的周长等于 .
 13. 定义:等腰三角形的顶角与其一个底角的度数的比值 称为这个等腰三角形的“特征值”.若等腰 中, ,则它的特征值 .14. 如图,已知 中, ,点 是线段 上的一动点,过点 作 交 于点 ,并使得 ,则 长度的取值范围是.
13. 定义:等腰三角形的顶角与其一个底角的度数的比值 称为这个等腰三角形的“特征值”.若等腰 中, ,则它的特征值 .14. 如图,已知 中, ,点 是线段 上的一动点,过点 作 交 于点 ,并使得 ,则 长度的取值范围是.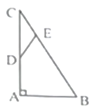 15. 如下图,在平面直角坐标系中,对 进行循环往复的轴对称变换,若原来点A坐标是 ,则经过第2019次变换后所得的A点坐标是.
15. 如下图,在平面直角坐标系中,对 进行循环往复的轴对称变换,若原来点A坐标是 ,则经过第2019次变换后所得的A点坐标是.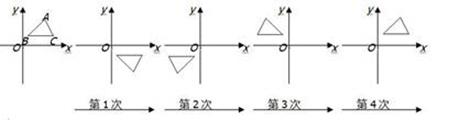
三、解答题
-
16. 已知:如图,AB=AD,BC=DC.求证:∠B=∠D.
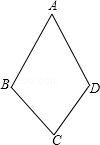 17. 如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长。为什么?
17. 如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使BC=CD,再画出BF的垂线DE,使E与A,C在一条直线上,这时测得DE的长就是AB的长。为什么? 18. 如图,在 中, .(1)、已知线段AB的垂直平分线与BC边交于点P,连结AP
18. 如图,在 中, .(1)、已知线段AB的垂直平分线与BC边交于点P,连结AP
求证: ;
(2)、以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q,连结AQ,若 ,求 的度数.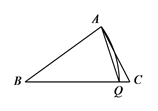 19. 如图,
19. 如图,
在△ABC中,AB=AC,点D、E分别在AB、AC上,BD=CE,BE、CD相交于点O;
求证:
(1)、(2)、20. 已知:如图,D是△ABC的BC边的中点,DE⊥AC,DF⊥AB,垂足分别为E、F,且DE=DF.求证:△ABC是等腰三角形.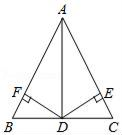 21. 如图,在 中, , 平分 .
21. 如图,在 中, , 平分 .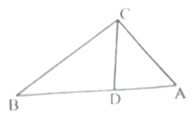 (1)、尺规作图:过点 作 边的垂线,垂足为点 (保留作图痕迹,不要求写作法);(2)、在(1)作出的图形中,求 的长.22. 如图,在等边三角形 的外侧作直线 ,点 关于直线 的对称点为点 ,连接 ,其中 交直线 于点 .
(1)、尺规作图:过点 作 边的垂线,垂足为点 (保留作图痕迹,不要求写作法);(2)、在(1)作出的图形中,求 的长.22. 如图,在等边三角形 的外侧作直线 ,点 关于直线 的对称点为点 ,连接 ,其中 交直线 于点 . (1)、依题意补全图形;(2)、已知 ,求 的度数.23. 如图①,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为直角边且在AD的上方作等腰直角三角形ADF,连接CF.
(1)、依题意补全图形;(2)、已知 ,求 的度数.23. 如图①,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为直角边且在AD的上方作等腰直角三角形ADF,连接CF.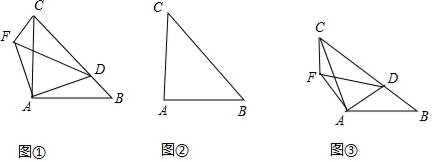 (1)、若AB=AC,∠BAC=90°
(1)、若AB=AC,∠BAC=90°①当点D在线段BC上时(与点B不重合),试探究CF与BD的数量关系和位置关系,并说明理由.
②当点D在线段BC的延长线上时,①中的结论是否仍然成立,请在图②中画出相应图形并直接写出你的猜想.
(2)、如图③,若AB≠AC,∠BAC≠90°,∠BCA=45°,点D在线段BC上运动,试探究CF与BC的位置关系,并说明理由.