2016-2017学年安徽省马鞍山市高一下学期期末数学试卷

试卷更新日期：2017-08-04 类型：期末考试

进入出卷网下载

一、选择题

1. 直线x﹣y+3=0的倾斜角是（）

A、30° B、45° C、60° D、135°

查看试题解析
2. 已知两条直线y=ax﹣2和y=x+1互相垂直，则a等于（）

A、2 B、1 C、0 D、﹣1

查看试题解析
3. 某工厂甲、乙、丙三个车间生产了同一种产品，数量分别为120件，80件，60件．为了解它们的产品质量是否存在显著差异，用分层抽样方法抽取了一个容量为n的样本进行调查，其中从丙车间的产品中抽取了3件，则n=（）

A、9 B、10 C、12 D、13

查看试题解析
4. 图中程序运行后输出的结果为（）

A、3，43 B、43，3 C、﹣18，16 D、16，﹣18

查看试题解析
5. 已知点P（x，y）在不等式组 ${\begin{matrix} x - 2 \leq 0 \\ y - 1 \leq 0 \\ x + 2 y - 2 \geq 0 \end{matrix}$ 表示的平面区域内运动，则z=x﹣y的最大值是（）

A、﹣1 B、﹣2 C、1 D、2

查看试题解析
6. 将容量为100的样本数据分为8个组，如下表：
组号
1
2
3
4
5
6
7
8
频数
10
13
x
14
15
13
12
9
则第3组的频率为（）

A、0.03 B、0.07 C、0.14 D、0.21

查看试题解析
7. 一个人打靶时连续射击两次，事件“至少有一次中靶”的互斥事件是（）

A、至多有一次中靶 B、两次都中靶 C、只有一次中靶 D、两次都不中靶

查看试题解析
8. 点P在边长为1的正方形ABCD内运动，则动点P到定点A的距离|PA|＜1的概率为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{π}{4}$ D、π

查看试题解析
9. A，B两名同学在5次数学考试中的成绩统计如下面的茎叶图所示，若A，B两人的平均成绩分别是x_A ， x_B ，观察茎叶图，下列结论正确的是（）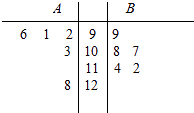

A、x_A＜x_B ， B比A成绩稳定 B、x_A＞x_B ， B比A成绩稳定 C、x_A＜x_B ， A比B成绩稳定 D、x_A＞x_B ， A比B成绩稳定

查看试题解析
10. 如图所示，程序框图的输出结果为（）

A、4 B、5 C、6 D、7

查看试题解析
11. 某小组有3名男生和2名女生，从中任选2名同学参加演讲比赛，那么至多一名女生参加的概率是（）

A、 $\frac{1}{10}$ B、 $\frac{3}{10}$ C、 $\frac{3}{5}$ D、 $\frac{9}{10}$

查看试题解析
12. 设两条直线的方程分别为x+y+a=0，x+y+b=0，已知a，b是方程x²+x+c=0的两个实根，且0≤c≤ $\frac{1}{8}$ ，则这两条直线之间的距离的最大值和最小值分别是（　　）

A、 $\frac{\sqrt{2}}{2}$ ， $\frac{1}{2}$ B、 $\sqrt{2}$ ， $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ ， $\frac{1}{2}$ D、 $\frac{\sqrt{2}}{4} ， \frac{1}{4}$

查看试题解析

二、填空题

13. 把十进制数23化为二进制数是．

查看试题解析
14. 从甲、乙、丙、丁四人中选3人当代表，则甲被选上的概率为．

查看试题解析
15. 设实数x，y满足 ${\begin{matrix} x - y - 2 \leq 0 \\ x + 2 y - 5 \geq 0 \\ y - 2 \leq 0 \end{matrix}$ ，则μ= $\frac{y}{x}$ 的取值范围是．

查看试题解析
16. 点（0，2）关于直线l：x+y﹣1=0的对称点的坐标为．

查看试题解析
17. 已知某8个数据的平均数为5，方差为3，现又加入一个新数据5，此时这9个数据的方差为．

查看试题解析

三、解答题

18. 已知直线l与直线2x﹣y+1=0平行，且过点P（1，2），求直线l的方程．

查看试题解析
19. 某射手平时射击成绩统计如表：
环数
7环以下
7
8
9
10
概率
0.13
a
b
0.25
0.24
已知他射中7环及7环以下的概率为0.29．

(1)、求a和b的值；

(2)、求命中10环或9环的概率；

(3)、求命中环数不足9环的概率．

查看试题解析
20. 下表是某厂的产量x与成本y的一组数据：
产量x（千件）
2
3
5
6
成本y（万元）
7
8
9
12
（Ⅰ）根据表中数据，求出回归直线的方程 $\hat{y}$ = $\hat{b}$ x $+ \hat{a}$ （其中 $\hat{b}$ = $\frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a}$ = $\bar{y}$ ﹣ $\hat{b} \bar{x}$ ）
（Ⅱ）预计产量为8千件时的成本．

查看试题解析
21. 2017年3月14日，“ofo共享单车”终于来到芜湖，ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台，开创了首个“单车共享”模式．相关部门准备对该项目进行考核，考核的硬性指标是：市民对该项目的满意指数不低于0.8，否则该项目需进行整改，该部门为了了解市民对该项目的满意程度，随机访问了使用共享单车的100名市民，并根据这100名市民对该项目满意程度的评分，绘制了如下频率分布直方图：
（I）为了了解部分市民对“共享单车”评分较低的原因，该部门从评分低于60分的市民中随机抽取2人进行座谈，求这2人评分恰好都在[50，60）的概率；
（II）根据你所学的统计知识，判断该项目能否通过考核，并说明理由．
（注：满意指数= $\frac{满意程度的平均得分}{100}$ ）

查看试题解析
22. 已知直线l：kx﹣y+1+2k=0（k∈R）
（Ⅰ）证明直线l经过定点并求此点的坐标；
（Ⅱ）若直线l不经过第四象限，求k的取值范围；
（Ⅲ）若直线l交x轴负半轴于点A，交y轴正半轴于点B，O为坐标原点，设△AOB的面积为S，求S的最小值及此时直线l的方程．

查看试题解析

组号	1	2	3	4	5	6	7	8
频数	10	13	x	14	15	13	12	9

环数	7环以下	7	8	9	10
概率	0.13	a	b	0.25	0.24

产量x（千件）	2	3	5	6
成本y（万元）	7	8	9	12