河北省保定市高阳县2016-2017学年八年级下学期期末考试数学试题
试卷更新日期:2017-08-04 类型:期末考试
一、选择题.
-
1. 下面各点在函数y= +1的图象上的是( )A、(2,1) B、(﹣2,1) C、(2,0) D、(﹣2,0)2. ▱ABCD中,如果∠B=100°,那么∠A、∠D的值分别是( )A、∠A=80°,∠D=100° B、∠A=100°,∠D=80° C、∠B=80°,∠D=80° D、∠A=100°,∠D=100°3. 若 ,则( )A、 B、 C、 D、4. 下列函数经过一、二、四象限的是( )A、 B、 C、 D、5. 下列二次根式不能与 合并的是( )A、 B、 C、 D、6. 在△ABC中,AB=1,AC= ,BC=2,则这个三角形是( )A、等腰直角三角形 B、等腰三角形 C、钝角三角形 D、直角三角形7. 下列计算错误的是( )A、× = B、+ = C、÷ =3 D、=8. 数据2、4、4、5、5、3、3、4的众数是( )A、1 B、2 C、3 D、49. 关于▱ABCD的叙述,正确的是( )A、若AB⊥BC,则▱ABCD 是菱形; B、若AC⊥BD,则▱ABCD 是正方形; C、若AC=BD,则▱ABCD 是矩形; D、若AB=AD,则▱ABCD 是正方形;10. 一次函数y=kx-k(k<0)的图象大致是( )A、
 B、
B、 C、
C、 D、
D、 11.
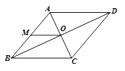
11.如图,M是菱形ABCD的边AB中点,MO=5cm,则菱形ABCD的周长为( )
 A、5 cm B、10 cm C、20 cm D、40 cm12. 已知一个直角三角形的两边长分别为3和5,则第三边长是( )A、5 B、4 C、 D、4或13.
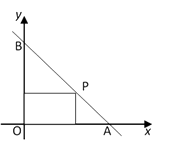
A、5 cm B、10 cm C、20 cm D、40 cm12. 已知一个直角三角形的两边长分别为3和5,则第三边长是( )A、5 B、4 C、 D、4或13.如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是( )
 A、 B、. C、 D、14. 已知:一组数据x1 , x2 , x3 , x4 , x5的平均数是2,方差是 ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )A、2, B、2,1 C、4, D、4,315. 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为( )
A、 B、. C、 D、14. 已知:一组数据x1 , x2 , x3 , x4 , x5的平均数是2,方差是 ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )A、2, B、2,1 C、4, D、4,315. 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为( )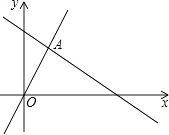 A、x≥ B、x≤3 C、x≤ D、x≥316.
A、x≥ B、x≤3 C、x≤ D、x≥316.如图,将边长为8㎝的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN , 则线段CN的长是( )
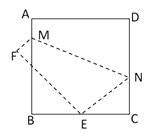 A、3cm B、4cm C、5cm D、6cm
A、3cm B、4cm C、5cm D、6cm二、填空题
-
17. 若两个连续整数 满足 ,则 的值是 ;18.
如下图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm到D,则橡皮筋被拉长了cm;
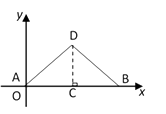 19.
19.如图,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是
 20.
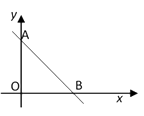
20.如图,直线 与 轴、 轴分别交于点B、A,在x轴上有点P,使得AB=BP,则点P的坐标为 .
三、解答题
-
21. 计算
(1)、(2)、
22.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
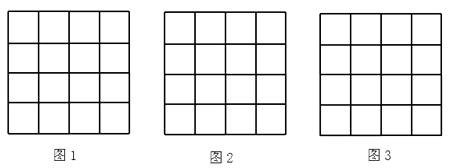 (1)、在图1中,画一个三角形,使它的三边长都是有理数;(2)、在图2中,画一个三角形,使它的三边长分别为3,2 , ;(3)、在图3中,画一个三角形,使它的三边都是无理数,并且构成的三角形是直角三角形。23.
(1)、在图1中,画一个三角形,使它的三边长都是有理数;(2)、在图2中,画一个三角形,使它的三边长分别为3,2 , ;(3)、在图3中,画一个三角形,使它的三边都是无理数,并且构成的三角形是直角三角形。23.如图,在四边形ABCD中,AD∥BC,∠B=90°,AG∥CD交BC于点G,点E、F分别为AG、CD的中点,连接DE、FG.
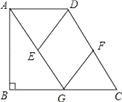 (1)、求证:四边形DEGF是平行四边形;(2)、当点G是BC的中点时,求证:四边形DEGF是菱形.24.
(1)、求证:四边形DEGF是平行四边形;(2)、当点G是BC的中点时,求证:四边形DEGF是菱形.24.如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1 , l2交于点C.
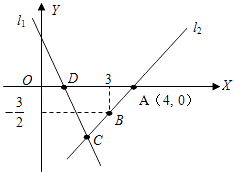 (1)、求点D的坐标;(2)、求直线l2的解析表达式;(3)、求△ADC的面积;(4)、在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.25.
(1)、求点D的坐标;(2)、求直线l2的解析表达式;(3)、求△ADC的面积;(4)、在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.25.甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.
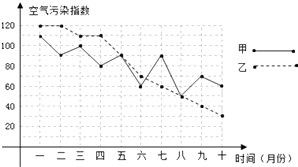 (1)、填写下表:
(1)、填写下表:平均数
方差
中位数
空气质量为优的次数
甲
80
340
1
乙
1060
80
3
(2)、从以下四个方面对甲、乙两城市的空气质量进行分析.①从平均数和空气质量为优的次数来分析甲乙两城市的空气质量哪个好一些;
②从平均数和中位数来分析甲乙两城市的空气质量哪个好一些;
③从平均数和方差来分析甲乙两城市的空气质量变化情况;
④根据折线图上两城市空气污染指数的走势来分析甲乙两城市的空气质量哪个好一些。
26.某市政府为了增强城镇居民抵御大病风险的能力,积极完善城镇居民医疗保险制度,纳入医疗保险的居民,大病住院医疗费用的报销比例标准如下表:
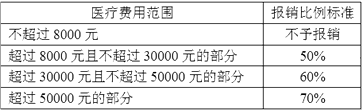
设享受医保的某居民一年的大病住院医疗费用为x元,按上述标准报销的金额为 y元.
(1)、直接写出x≤50000时,y关于x的函数关系式,并注明自变量x的取值范围;(2)、若某居民大病住院医疗费用按标准报销了20000元,问他住院医疗费用是多少元?