河北省唐山市路南区2016-2017学年八年级下学期期末质量检测数学试题
试卷更新日期:2017-08-04 类型:期末考试
一、选择题
-
1. 等于( )
A、4 B、±4 C、-4 D、±22. 函数 中,自变量x的取值范围是( )A、x>-3 B、x≥-3 C、x≠-3 D、x≤-33. 一次函数y=-2x-1的图象大致是( )A、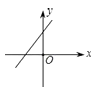 B、
B、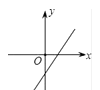 C、
C、 D、
D、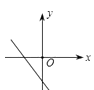 4. 下列命题正确的是( )A、对角线相等的四边形是矩形 B、对角线互相垂直且相等的四边形是正方形 C、对角线互相垂直的四边形是菱形 D、对角线互相平分的四边形是平行四边形5.
4. 下列命题正确的是( )A、对角线相等的四边形是矩形 B、对角线互相垂直且相等的四边形是正方形 C、对角线互相垂直的四边形是菱形 D、对角线互相平分的四边形是平行四边形5.学校准备设计一款女生校服,对全校女生喜欢的颜色进行了问卷调查,统计如下表所示:

学校决定采用红色,可用来解释这一现象的统计知识是( )
A、平均数 B、中位数 C、众数 D、方差6. 在图形旋转中,下列说法错误的是( )A、旋转中心到对应点的距离相等 B、图形上的每一点转动的角度相同 C、图形上可能存在不动点 D、图形上任意两点的连线与其对应两点的连线相等7. 如图,在矩形ABCD中,对角线AC、BD交于点O , 以下说法错误的是( ) A、 B、 C、 D、8. 下列计算正确的是( )A、 B、 C、 D、9. 如图,菱形ABCD的边长是2,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
A、 B、 C、 D、8. 下列计算正确的是( )A、 B、 C、 D、9. 如图,菱形ABCD的边长是2,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( ) A、 B、 C、2 D、10.
A、 B、 C、2 D、10.梅梅以每件6元的价格购进某商品若干件到市场去销售,销售金额y(元)与销售量x(件)的函数关系图象如图所示,则降价后每件商品的销售利润为( )
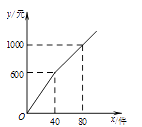 A、4元 B、5元 C、10元 D、15元11. 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A , 则不等式组 的解集为( )
A、4元 B、5元 C、10元 D、15元11. 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A , 则不等式组 的解集为( ) A、x<1 B、x>2 C、0<x<2 D、0<x<112. 数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是 ,这种说明问题的方式体现的数学思想方法叫做( )
A、x<1 B、x>2 C、0<x<2 D、0<x<112. 数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是 ,这种说明问题的方式体现的数学思想方法叫做( ) A、代入法 B、换元法 C、数形结合 D、分类讨论
A、代入法 B、换元法 C、数形结合 D、分类讨论二、填空题
-
13. 直线y= x与x轴交点的坐标是 .14. 如图,正方形ABCD中,AE⊥BE于E , 且AE=3,BE=4,则阴影部分的面积是 .
 15.
15.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°),若∠1=110°,则∠α= .
 16. 如图,直线 和x=3的交点坐标是 .
16. 如图,直线 和x=3的交点坐标是 . 17.
17.已知小明家5月份总支出共计5000元,各项支出所占百分比如图所示,那么用于教育的支出是元.
 18. 已知y是x的函数,在y=(m+2)x+m-3中,y随x的增大而减小,图象与y轴交于负半轴,则m的取值范围是 .
18. 已知y是x的函数,在y=(m+2)x+m-3中,y随x的增大而减小,图象与y轴交于负半轴,则m的取值范围是 .三、解答题
-
19. 计算:(1)、;(2)、 .20.
如图,在平面直角坐标系中,有一Rt△ABC , 且点A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.
 (1)、旋转中心的坐标是 , 旋转角的度数是 .(2)、以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°,180°的三角形.
(1)、旋转中心的坐标是 , 旋转角的度数是 .(2)、以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°,180°的三角形.
(3)、利用变换前后所形成的图案,可以证明的定理是 .21.某总公司为了评价甲、乙两个分公司去年的产值,统计了这两个分公司去年12个月的产值(单位:万元)情况,分别如下图所示:
 (1)、利用上图中的信息,完成下表:
(1)、利用上图中的信息,完成下表:平均数
中位数
众数
方差
甲
8
8
3
乙
8
9
1.5
(2)、假若你是公司的总经理,请你从以下三个不同的角度对两个分公司的产值进行分析,对两个分公司做出评价;①从平均数和众数相结合看(分析哪个公司产值好些);
②从平均数和中位数相结合看(分析哪个公司产值好些).
③从平均数和方差相结合看(分析哪个公司产值好些).
22. 如图,直线l: 与x轴、y轴分别交于点A、B , 点P1(2,1)在直线l上,将点P1先向右平移1个单位,再向上平移2个单位得到像点P2 . (1)、判断点P2是否在直线l上;并说明理由.(2)、若直线l上的点在x轴上方,直接写出x的取值范围.(3)、若点P为过原点O与直线l平行的直线上任意一点,直接写出S△PAB的值.23. 如图,点O是△ABC内一点,连结OB、OC , 并将AB、OB、OC、AC的中点D、E、F、G依次连接,得到四边形DEFG .
(1)、判断点P2是否在直线l上;并说明理由.(2)、若直线l上的点在x轴上方,直接写出x的取值范围.(3)、若点P为过原点O与直线l平行的直线上任意一点,直接写出S△PAB的值.23. 如图,点O是△ABC内一点,连结OB、OC , 并将AB、OB、OC、AC的中点D、E、F、G依次连接,得到四边形DEFG . (1)、求证:四边形DEFG是平行四边形;(2)、如果∠BOC=90°,∠OCB=30°,OB=2,求EF的长.
(1)、求证:四边形DEFG是平行四边形;(2)、如果∠BOC=90°,∠OCB=30°,OB=2,求EF的长.
24. 小李从甲地前往乙地,到达乙地休息了半个小时后,又按原路返回甲地,他与甲地的距离 y (千米)和所用的时间 x (小时)之间的函数关系如图所示. (1)、小王从乙地返回甲地用了多少小时?(2)、求小李出发6小时后距离甲地多远?(3)、在甲、乙两地之间有一丙地,小李从去时途经丙地,到返回时路过丙地,共用了2小时50分钟,求甲、丙两地相距多远?25. 如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,
(1)、小王从乙地返回甲地用了多少小时?(2)、求小李出发6小时后距离甲地多远?(3)、在甲、乙两地之间有一丙地,小李从去时途经丙地,到返回时路过丙地,共用了2小时50分钟,求甲、丙两地相距多远?25. 如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等, (1)、求∠EAF的度数;(2)、在图①中,连结BD分别交AE、AF于点M、N,将△ADN绕点A顺时针旋转90°至△ABH位置,连结MH,得到图②.求证:MN2=MB2+ ND2;(3)、在图②中,若AG=12, BM= ,直接写出MN的值.
(1)、求∠EAF的度数;(2)、在图①中,连结BD分别交AE、AF于点M、N,将△ADN绕点A顺时针旋转90°至△ABH位置,连结MH,得到图②.求证:MN2=MB2+ ND2;(3)、在图②中,若AG=12, BM= ,直接写出MN的值.